阿基米德Copula函数的拟合检验

李述山

0 引言

Copula函数是连接随机变量边缘分布的累积分函数，描述了变量间的相关结构[1][6]。运用Copula技术来分析随机变量间的相关性有很多优点：一是Copula模型不限制边缘分布的选择，而且Copula函数有很多分布族；二是Copula模型可以将随机变量之间的相关程度和相关模式有机地结合在一起，不仅可以得到度量相关程度的相关参数，还可以得到描述相关模式的Copula函数，因此可以更全面地刻画随机变量间的相关关系，如Kendall的τ、上尾相关系数与下尾相关系数等。因此，在金融资产间的相关性分析、金融资产及资产组合的风险评估、可靠性评估等方面得到了广泛应用。

常用的Copula函数总体可以分为椭圆型copulas和阿基米德copulas，而每一族又分为许多具体的连接函数类。不同的copula有不同的性质，椭圆copula函数族具有对称的尾部相关性，这与金融数据的厚尾分布相违背。阿基米德copula函数族具有以下特性：构建且计算简单，多种不同的copula都归属于这个函数族中；对数收益率的相关性结构符合阿基米德copula分布[2]。在运用阿基米德Copula研究实际问题的过程中，有一个重要问题就是阿基米德Copula函数的选择。要选择能正确描述变量间相关结构的Copula函数，我们就必须对阿基米德Copula函数的拟合度进行评价，即对所选择的Copula函数进行拟合检验。

本文拟介绍阿基米德Copula已有的两种检验方法，并建立新的检验方法，通过进行模拟检验，说明新检验法的优良性。

1 阿基米德Copula函数拟合检验的两种常见检验方法

1.1 基于Rosenblatt积分变换的K-S检验法

定理1[3]令 X=(X1,X2,…,Xd)为一随机向量，记T(x)=(T1(x1),T2(x2),…,Td(xd))

其中:

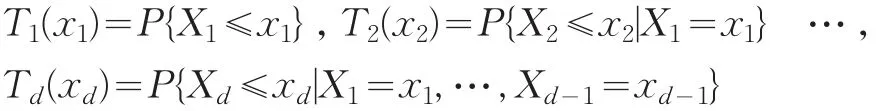
则 T1(X1),T2(X2),…,Td(Xd)相互独立，皆服从U(0,1)。

推论1[1]设随机向量(U,V)的边缘分布皆为(0,1)上的均匀分布，联合分布函数为阿基米德copulas C(u,v;θ)，生成元为 φ(t;θ)，则 C1(U,V;θ)～U(0,1)，且与U 独立，其中 C1(u,v;θ)=φ'(u;θ)/φ'(C(u,v;θ);θ)。

由推论 1 可知，假设检验问题 H0:(U,V)～C(u,v;θ̂)可转化为假设检验问题：

H0:C1(U,V;θ̂)～U(0,1) 对 H1:C1(U,V;θ̂) 不 服 从U(0,1)

该假设检验问题常采用如下的K-S检验法：

设(U,V)为二维随机向量，U,V～U(0,1)，连接函数为 C(u,v;θ)，(ui,vi),i=1,…,n 为来自 (U,V)的样本（观 察 值），记 wi=C1(ui,vi;θ̂),i=1,…,n ， Fn(x)为wi,i=1,…,n相应的经验分布函数，取作为检验统计量，对检验水平α，当Dn＞Dn(α)时拒绝原假设。

称该检验法为基于Rosenblatt积分变换的K-S检验法。

1.2 基于copula变换与概率积分变换的K-S检验法

定理2[1]设随机向量(U,V)的边缘分布皆为(0,1)上的均匀分布，联合分布函数为阿基米德copulas C(u,v;θ)，生成元为 φ(t;θ)，则（1）C(U,V;θ)的分布函数为 KC(t;θ)=t- φ(t;θ)/φ'(t+;θ)；（2）Kc(C(U,V;θ);θ)～U(0,1)；（3）设 (Ui,Vi),i=1,2,…,n为来自 (U,V)的样本，记KC(C(Ui,Vi;θ);θ),i=1,2,…,n ，则 Wi,i=1,2,…,n 相互独立且皆服从(0,1)上的均匀分布。

由定理 2 可知，假设检验问题 H0:(U,V)～C(u,v;θ̂)可转化为假设检验问题：

H0:Kc(C(U,V;θ̂); θ̂)～U(0,1) 对 H1:Kc(C(U,V;θ̂);θ̂)不服从 U(0,1)

该假设检验问题常采用如下的K-S检验法：

设(U,V)为二维随机向量，U,V～U(0,1)，连接函数为C(u,v;θ)，(ui,vi),i=1,…,n为来自(U,V)的样本（ 观 察 值 ），记 wi=KC(C(ui,vi;θ̂);  θ̂ ), i=1,2,…,n ，Fn(x)为 wi,i=1,…,n相应的经验分布函数，取作为检验统计量，对检验水平α，当Dn＞Dn(α)时拒绝原假设。

称该检验法为基于copula变换与概率积分变换的K-S检验法。

2 阿基米德Copula函数拟合检验的两种新方法

2.1 基于一种函数变换的K-S检验法

定理3[1]设随机向量(U,V)的边缘分布皆为(0,1)上的均匀分布，联合分布函数为阿基米德copula C(u,v;θ)，生 成 元 为 φ(t;θ) ，记 S=φ(U;θ)/(φ(U;θ)+φ(V;θ)) ，T=C(U,V;θ)，则：

（1）(S,T)的联合分布函数为：

（2）S～U(0,1)且S与T独立。

由定理3可以知道，S(θ)=φ(U;θ)/(φ(U;θ)+φ(V;θ))～U(0,1)，因此假设检验问题 H0:(U,V)～C(u,v;θ̂)可转化为假设检验问题：

H0:S(θ̂)～U(0,1) 对 H1:S(θ̂)不服从 U(0,1)

该假设检验问题可以采用K-S检验法，称为基于一函数变换的K-S检验法。

2.2 基于随机向量变换的χ2拟合优度检验法

推论2设随机向量(U,V)的边缘分布皆为(0,1)上的均匀分布，联合分布函数为阿基米德copulas C(u,v;θ)，生成 元 为 φ(t;θ) ，则 S(θ)=φ(U;θ)/(φ(U;θ)+φ(V;θ)) 与W(θ)=KC(C(U,V;θ);θ)独立，且皆服从 (0,1)上的均匀分布。

由推论 2 知，假设检验问题 H0:(U,V)～C(u,v;θ̂)可转化为假设检验问题：

H0:(S(θ̂),W(θ̂)) 服从 (0,1)2上均 匀分 布 对 H1:(S(θ̂),W(θ̂))不服从 (0,1)2上均匀分布。

对该问题我们采用与文[7]类似的χ2拟合优度检验法：设(U,V)为二维随机向量，U,V～U(0,1)，连接函数为C(u,v;θ)，(ui,vi),i=1,…,n为来自(U,V)的样本（观察 值 ） ，记 xi= φ(ui;θ̂)/(φ(ui;θ̂)+ φ(vi;θ̂)),yi=KC(C(ui,vi;θ̂);θ̂),i=1,2,…,n 。将 (0,1)2均匀分割成 m× m个 单 元 格 G(i,j)，i,j=1,2,…,m ，记 nij为(xi,yi),i=1,2,…,n落入单元格G(i,j)内的频数，则在原假设H0成立时，统计量渐进服从自由度为 m2-1的 χ2分布。对检验水平 α，当M＞χ2α(m2-1)时拒绝原假设。

称该检验法为基于随机向量变换的χ2拟合优度检验法。

3 模拟检验与分析

本文选用二元Clayton Copula与二元Gumbel Copula以考察4种检验法的检验效果。

针对二元Clayton Copula与二元Gumbel Copula（分布函数记为C(u,v;θ)，在参数真值为θ=5下分别随机产生C(u,v;θ)的2000个样本，参数估计值为设定的7个值：θ̂=4.0,4.5,4.7,5.0,5.3,5.5,6.0 ，采用以上4种检验方法分别在检验水平0.05、0.01下进行检验，检验问题为：H0:(U,V)～C(u,v;θ̂)对 H1:(U,V)不服从分布 C(u,v;θ̂)

共进行模拟检验100次，记录接受原假设的次数，结果见表1、表2。

表2 Gumbel Copula的模拟检验结果

4 结论与分析

本文首先介绍了已有的两种检验方法：基于Rosenblatt积分变换的K-S检验法与基于copula变换及概率积分变换的K-S检验法，进一步建立了两个新的检验方法--基于一种函数变换的K-S检验法与基于随机向量变换的χ2拟合优度检验法，并进行了模拟检验，从模拟检验的过程及结果，可得如下分析及建议。

（1）四种检验法只适用于二元阿基米德copulas的检验，不能用于多元阿基米德copulas的检验。

（2）从表1与表2的检验结果可以看出：①基于Rosenblatt积分变换的K-S检验法与基于一种函数变换的K-S检验法效果相近，但基于一种函数变换的K-S检验法更为直接、简单；②基于随机向量变换的χ2拟合优度检验法最严格，且检验结果符合实际，原因是该检验法利用了样本的全部信息，不仅对变换后的边缘分布而且对独立性进行了检验；③基于copula变换与概率积分变换的K-S检验法效果较差，究其原因，是因为该检验法只是利用了样本的部分信息。

（3）鉴于如上两点，我们认为不宜采用基于copula变换与概率积分变换的K-S检验法。

[1]Nelsen RB.An Introduction to Copulas[M].New York:Springer,1999.

[2]JOE H.Multivariate Models and Dependence Concepts[M].London:Chapman and Hall,1997.

[3]Rosenblatt M.Remarks on a Multivariate Transformation[J].Annals of Mathematical Statistics,1952,(23）.

[4]Fermanian JD.Goodness-of-fit Tests for Copulas[J].Journal of Multi⁃variate Analysis,2005,(95).

[5]Genest C,Rivest L.Statistical Inference Procedures for Bivariate Ar⁃chimedean Copulas[J].Journal of the American Statistical Associa⁃tion,1993,(88).

[6]张尧庭.连接函数(Copula)技术与金融风险分析[J].统计研究，2002，(4).

[7]李述山.Copula函数拟合检验的一种新方法[J].统计与决策，2010,(24).