基于PLS算法的带缺失值顾客满意度指数的测评

赵富强刘金兰

0 引言

顾客满意度是一个经济心理学的概念，是用消费者的消费经验来衡量产品和服务的质量的。顾客满意度视为一个不能被直接观测潜变量，因此在测评中将总体用多重指标的方法来测量，测量结果是潜变量的分数，可以用于各个公司、行业、部门、地区和国家的顾客满意度情况的比较。但在进行顾客满意度调查时，研究人员得到的实际数据往往存在丢失的问题。当数据缺失后，在计算变量间的相关系数或协方差时，需要考虑如何对缺失值进行处理。

1 缺失值产生的原因、方式及处理方法

缺失值是指在进行问卷抽样调查或实验性研究中，应该从抽样的样本单元中得到而实际上却由于种种原因而未得到所需的数据，也称为缺失数据。

在进行实验性研究或问卷抽样调查中，数据缺失现象经常发生，主要原因包括：①被调查者不愿提供调查所需要的信息；②不可人为控制的因素造成数据的缺失；③调研人员本身或调查系统的原因没有收集到完全的信息；④信息填报汇总错误原因造成数据的缺失等。产生缺失数据原因多种多样，实际工作中有时很难判断和检测缺失数据产生的机制与方式。为了认识和研究缺失的数据，从形式上将其分为单元缺失与项目缺失两种。Little和Rubin[2]定义了三种不同的数据缺失机制，即完全随机缺失(MCAR)、随机缺失（MAR）和不可忽略的缺失（NIM）。整个缺失数据的推估过程中，缺失数据的情况表现为三种方式[4,5]，即单变量缺失、单调缺失型和任意缺失型。

缺失值的处理方法主要包括Ad Hoc法和缺失值插补法。Ad Hoc法通常将有缺失值的数据整列删除或成对删除，它是缺失值处理最常用的方法，尽管简单，但当数据缺失率低的情况下，仍具有一定优势，包括如下两种：

（1）列删除法

列删除法是指在收集到的样本中如果含有缺失数据，则把含有缺失数据的记录删除。

（2）成对删除法

在计算两个变量的相关系数时，若其中一个变量有缺失数据，则删除这条记录，同时也删除另一个变量对应的记录（即使该变量数据完全）。该方法多用在因子分析、重复测量设计、区组设计资料分析及回归与相关分析中。

缺失值插补法包括：均值插补法、随机插补法和多重插补方法等，在此不作阐述。

除上述方法外，缺失值处理还有回归或主成分法、最大似然估计法[5]、相似反应模式设算法和MCMC算法等。

在文献[6]中，Lohmöller’s PLSX对缺失值的处理为：⑴如果所有的显变量样本值都缺失，那么该样本无效，无法估计潜变量。⑵如果该块的显变量样本值不全缺失，那么计算潜变量估计时，缺失的显变量值由该显变量的均值替代。⑶如果该潜变量估计值有缺失，那么计算内部估计时，缺失值由0替代。⑷权重的计算：①模式A（Mode A）：权重根据公式计算；②模式B（Mode B）：当没有缺失值按照公式计算；有缺失值时，采用成对删除法把对应的缺失样本值删除，即不考虑在内，然后利用公式来计算权重。

2 求解带缺失值的顾客满意度指数

在ACSI顾客满意度指数模型中，ξr为潜（隐）变量，ξ0为潜自变量（外生变量），其他为潜因变量（内生变量）；xrt为显变量（观测变量，r=0,1,2,3,4,5），即为ξr的指标，t为潜变量对应观测值的个数(t=1,2…kr，kr为第r个潜变量对应观测值的个数)，LXr分别为潜变量ξr的PLS估计值。

求解带缺失值的顾客满意度指数步骤如下：

（1）异常值处理

所谓异常值是被调查顾客在回答问卷时，由于各种原因而选择了“不知道”、“拒绝回答”以及“超出数值范围”等选项时系统默认的值。问卷采用10分制，从1分到10分供被调查者选择，且只能选择一个。对被调查者不知道或拒绝的回答，在数据库里进行了标识（98表示不知道；99表示拒绝；101表示从来不购买）。这些数据在进行处理时按照缺失值处理。

（2）数据标准化

使得样本值的均值为0、方差为1。

（3）缺失值处理

对数据库里面的缺失值（在数据库里标记为NaN）用0代替。初始化的权重分别为：v（1，0，0）、w1（1，0，0）、w2（1，0）、w3（1，0，0）、w4（1）、w5（1，0）。在一个块结构中，只要有一个显变量的值没有缺失，那么就不删除该样本，处理的方法是“权重新定”。“权重新定”的方法是只要该潜变量对应的显变量中的样本数据不全为0，那么该样本即代表的被调查对象对问题的态度，不能对该样本做简单的删除处理；对显变量为0的权重在计算时不考虑在内，显变量不为0权重在原有权重及总和为1的基础上进行重新计算。

设一n维权重列向量W=(ω1,…,ωn)，ω1+…+ωn=1；现在有一个包括n个数据的行向量X=(x1,…,xn)，其中第i，j个数据缺失，“权重新定”的计算公式为：

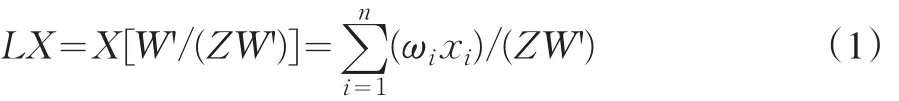
其中，Z是第i，j位置上为0，其余为1，包括n个数据的行向量；W’为列向量的转置。

例如：样本X=(0,5,10,0)，其对应权重W=(1/4,1/2,1/8,1/，LX=(0,5,10,0)(2/5,4/5,1/5,1/5)’=6，即x1=x4=0，其权重不考虑，对x2，x3的权重重新计算。

（4）利用PLS算法来估计模型中各个参数

计算过程参见下节，反复迭代得到潜变量估计值。

（5）求出顾客满意度指数

根据第（4）步求得的权重系数，计算出顾客满意度指数[1]。

3 Wold’s PLS算法模型估计[3]

需要指出的是，含多个潜变量结构方程模型的块结构设定原则是假定块内每个指标分别与对应的潜变量存在线性关系。模型设定详细步骤在此不再给出。

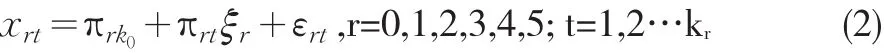
其中，πrt为指标xrt的载荷系数(测量模型系数)，εrt为残差，πrk0为截距值，kr为第r个潜变量对应观测值的个数。

含多个潜变量结构方程模型的内部关系设定原则是内部关系应该构成一个线性因果链系统（linear causal chain system）。

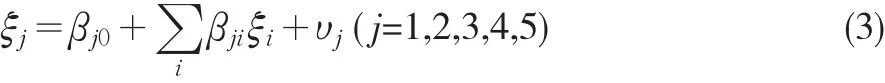
权重关系利用信息交换过程中的部分信息估计潜变量值。任何一个潜变量均可以通过其指标变量的加权和来估计，而权重则由所选择的权重关系来确定。每个潜变量权重关系可根据不同的情况包括模式A或模式B。

模式A权重关系为：

模式B权重关系为：

对ACSI路模型中潜变量ξr的符号权重和定义为Ur。假设与ξi邻接的潜变量是ξj，则公式为：

其中srj是LXr和LXj的带符号相关系数：

无缺失值时潜变量估计值的计算方法：

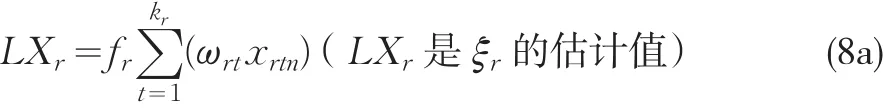
有缺失值时潜变量估计值的计算方法（权重新定）：

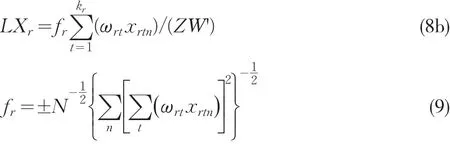
fr的正负符号选择取决于期望的相关关系。

以后，就可以利用PLS算法来估计模型中各个参数，进而求解出整个结构方程模型。这里取样本容量为N，指标xrt的样本观测值分别记为 xrtn，其中n=1…N，并且所有数据都已经标准化（均值为0，方差为1）。

模型设定完成以后，就可以利用PLS算法来估计模型中各个参数，进而求解出整个结构方程模型。这里取样本容量为N，指标xrt的样本观测值分别记为xrtn，其中n=1…N并且所有数据都已经标准化（均值为0，方差为1）。

基于ACSI模型的PLS算法主要分三步。

第一步，通过反复迭代得到潜变量估计值。

①设定初始权重ωrt(s)；

②利用ωrt(s)根据公式(9)计算 fr，进而根据公式(9)计算ξr的估计值LXr；

③利用LXr由公式(7)计算srj；

④利用srj根据公式(6)计算Ur；

⑤利用Ur根据公式(4)或(5)回归计算新的权重

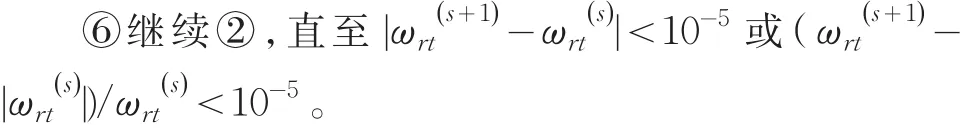
第二步，将由第一步得出的潜变量估计值LXr分别与对应的指标观测值回归，根据潜变量的估计值，利用公式(2)计算外部关系的载荷系数，利用公式(3)计算内部关系的回归系数。

（1）块结构参数的估计（外部关系）

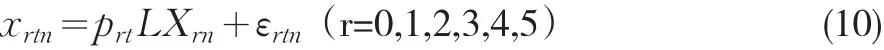
其中，εrtn为残差，prt为回归系数（测量模型系数）。

（2）内部关系参数的估计（内部关系）

其中，υrn为残差，b为回归系数（结构模型系数）。

第三步，求出均值，给出最初的关系式。

4 模型实例分析

以某食品公司为研究对象、ACSI为测评模型，利用基于Wold的PLS算法、处理缺失值采用“权重新定”的方法实现的顾客满意度测评系统（MyPLS）完成对采集样本的处理，处理步骤为：

（1）数据的收集采取网上调查的方式进行，参与网上调查的用户为252位，因此样本量为252（见表1）。

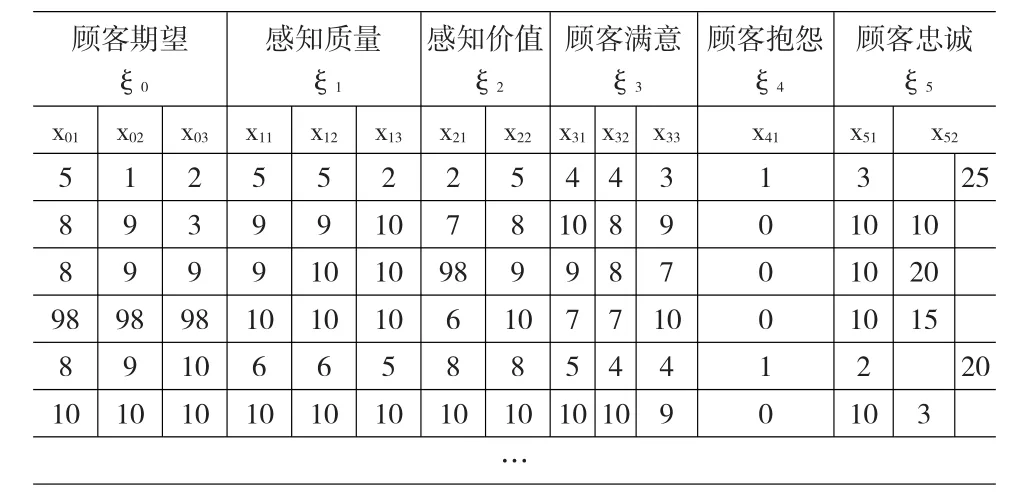
表1 某食品公司顾客满意度调查原始数据表

（2）表1中x52表示价格敏感度，包括价格上涨和价格下降，x52最后取值价格上涨+25或价格下降-25；表中的98、99、101用符号“NaN”替换，表示缺失数据。

（3）对原始数据标准化处理。

（4）“权重新定”的方法处理缺失值，计算潜变量的估计值，用PLS算法反复迭代求出权重系数，进而得到顾客满意度指数。

通过对带缺失值的数据进行实证分析得出：如果其它条件不变，在权重ω初始值改变，各ω值迭代结果收敛于一定数值，即最终的迭代结果是相同的，表明整个迭代过程是收敛的；Cronbach’sα系数均大于0.7，均在很可信范围；测评标准化因子负荷处于0.6107-0.9675之间，表明指标和潜变量间的有足够的线性等价关系，满足偏最小二乘法单一维度的条件；所有概念的AVE值都处于0.7138-0.9308之间，均大于0.5，这表明本文所设计的量表具有良好的内敛效度，见表2。

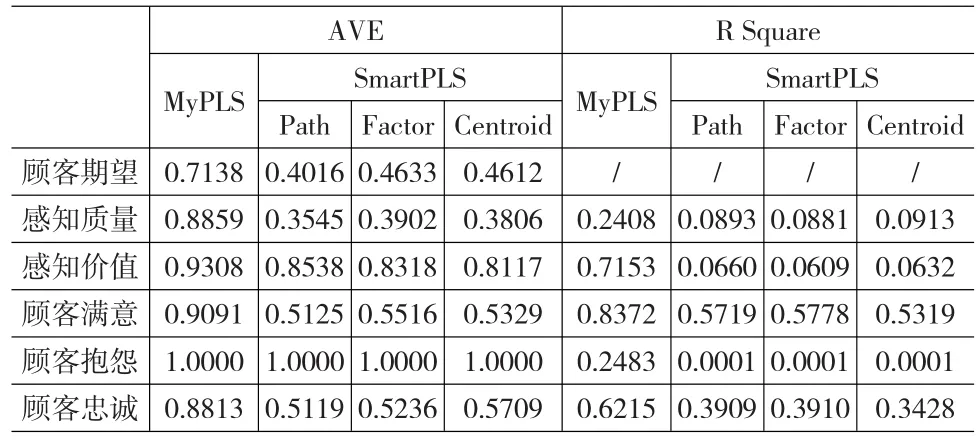
表2 模型评价参数比较

基于Java开发的SmartPLS[7]软件处理同样的样本，可以得出：SmartPLS软件的三种权重模式质心、因子和路径求解到收敛的迭代次数分别为9、13和13，本文的PLS算法求解测评模型（简称MyPLS）仅仅需要5次。因此，My-PLS系统提高了对模型分析处理速度，在结构模型系数，潜变量估计值相关系数，权重系数，测量模型系数等方面，MyPLS与SmartPLS具有一致性；但在路径系数、权重系数、公因子方差等个别项中有较大差异，可能是由于在缺失值处理方法不同导致的。

5 结论

本文分析了带缺失值的顾客满意度指数测评步骤：异常值处理、数据标准化、缺失值处理、利用PLS算法来估计模型中各个参数、求出顾客满意度指数等；提出了一种缺失值处理方法“权重新定”；通过对某食品公司的带缺失值数据分析，验证了“权重新定”的缺失值处理方法的有效性。

[1]Fornell C.，刘金兰.顾客满意度与ACSI[M].天津：天津大学出版社,2006.

[2]Little R J A,Rubin D B.Statistical Analysis with Missing Data[M].New York:John Wiley&Sons,2002.

[3]Wold H.Soft Modeling：The Basic Design and Some Extensions[A].K G J reskog H Wold，Systems under Indirect Observation[C].North-Holland：Amsterdam,1982.

[4]Wang Q H,Rao J N K.Empirical Likelihood for Linear Regression Models under Imputation for Missing Response[J].The Canadian Jour⁃nal Statistics,2001,(29).

[5]Allison,Paul D.Missingdata Techniquesfor Structural Equation mod⁃els[J].Journal of Abnormal Psychology,2003,112.

[6]Tenenhaus,M.,Vinzi,V.E.,Chatelin,Y.M.,Lauro,C.PLSPath Model⁃ing[J].Computational Statisticsand Data Analysis,2005,48(1).

[7]Ringle,C.M.,Wende,S.,Will,A.SmartPLS-Version 2.0.Universität Hamburg,Hamburg[Z].2005.