关于抽样调查中多层次调查问题的探讨

吕 萍

0 引言

抽样调查作为一种获取统计资料的重要手段，日益受到政府各部门、企业、学术界和社会公众的重视。由于中国各级政府都要管经济，各级行政长官都关心本地区的经济，都需要掌握有关统计数据，出现了如何满足多层次调查的需要，也就是多层次抽样调查的问题。此处的层次包含在抽样设计中的为了提高抽样效率利用辅助信息分的层，也包含行政设置中的省市、区县、村居等的自然层，也称为域，分层次调查问题是总体和各个层次（也称为域、子总体）都需要估计的问题。尤其是大型的抽样调查，例如中国科学素养调查、中国妇女的社会地位等大型综合调查都需要在对全国的目标变量进行估计的基础上也对各省(层次)的目标变量进行估计。

解决分层次调查问题的方法主要有直接估计方法和间接估计方法。其中直接估计方法主要有层层抽样的方法、ABC法[1]、样本追加法[2]。其中，层层抽样和ABC三级[1]一套的样本设计是一种自下而上的抽样思路，简单直接，但由于需要对所有的县都进行调查，经费庞大从而违背了抽样调查的经济性的优势，而且各个县的工作效率以及调查和估计很难统一等缺点，在实际应用中有很大的局限性。样本追加方法是一种自下而上抽样设计思路，是由冯世雍与秦怀振[3]于2002年提出的一种分层次抽样设计方法，是在满足上一级目标变量估计精度需要的基础上用样本追加的方法来满足下一级尤其是省级目标变量估计精度的需要。间接估计方法是充分挖掘已有的样本信息，充分利用间接信息和数据改进各个层次的目标变量的估计量，与传统数理统计中的时间序列、回归模型、贝叶斯统计等方法得到各个层次的目标变量的有效估计量。

1 分层次调查的抽样设计思路

在实践中主要有两种多层次调查问题。第一，总体和各层次的调查不同时进行，即总体调查在前，省级调查在后。第二，总体与省级调查总体的调查同时进行。从抽样设计的角度，有两种解决上述分层次调查问题的样本追加方法，一种是用冯世雍与秦怀振于2002年提出的样本追加方法，一种是利用永久随机数的方法来进行样本追加。

1.1 分层次调查中的样本追加方法

样本追加方法的基本思想是按照某种特定的概率抽样方法，从总体中抽取样本对总体的目标变量进行估计。但对于其中的某些层或域，由于落入该层的样本单元不能保证对该层或域的目标量推断的需要，即落入其中的样本对该层或域没有代表性，此时在该层内按照某种抽样方法追加部分样本单元与原来落入该层或域的样本（主体样本）组成复合样本来对该层的目标量进行推断，通过样本追加满足来下一层目标量估计的需要，两级样本相互兼容，同时利用这些追加的样本还可以进一步提高总体目标量的估计精度。

这种方法的优势主要体现在：（1）样本追加可以很好地实现多级样本的兼容，以提高样本的使用效率，节约调查成本；（2）样本追加避免各个层都要抽样带来的人力物力财力的浪费，只在有推断要求的层追加样本。（3）样本追加可以进一步提高上级目标变量的估计精度。

多层次调查中的样本追加将抽样设计分为主体设计，追加设计和终极设计。为确保总体推断的可靠性而制定的抽样设计称为主体设计，为确保对某种层推断的可靠性而为需要追加层制定的抽样设计称为域追加设计。主体设计和追加设计连同实施方案一起的抽样设计称为终极设计。

当总体的抽样设计与层的追加设计独立进行、独立实施，利用终极样本对总体以及需要估计的层（层）的目标变量进行估计的样本追加方法称为独立样本追加方法。在实施主体设计的基础上在层进行样本追加，对总体以及层的目标变量的估计称为条件样本追加。不管是独立追加设计还是条件追加设计，其基本的设计思想是根据主体的抽样设计和层的样本追加设计分别构造总体和层的参数估计并选择合适的方差估计方法；然后构造总体和层参数的估计类，在类内选择最优伪估计，构造渐进局部最优估计，从而得到层的目标变量的最优估计量。

在实际调查中，独立样本追加是易于操作的样本追加方法，只需将主体设计和层的追加设计按照各自的抽样方案独立设计、独立进行、独立设施，相当于做了两次独立的抽样调查，然后利用极小化方差的思想，在主体设计与追加设计都可测并满足最小方差的前提下，基于主体样本和追加样本分别构造总体的目标变量的H－T估计量及其方差估计量，最后利用极小方差的方法在层的线性无偏类中找到目标变量的最优估计量。以总量估计为例，利用总体总量Y的H－T估计Ŷπ和层的总量YD的H－T估计ŶDπ及其方差估计量，层追加样本的总量估计量Ŷ+Dπ及其方差的无偏估计量；然后通过极小化方差的方法在YD的线性无偏类 {ŶD(θ)=θŶDπ+(1-θ)ŶDπ+;θ∈R}里找到局部最优伪估计；最后通过估计其方差里的未知系数来构造层总量的渐进局部最优估计。

由上得到

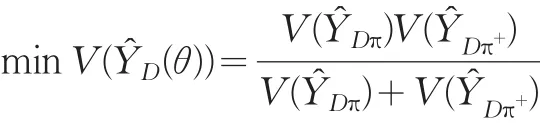
得到独立追加在追加设计可测的情况下，层的估计量ŶD(θ)的最有方差估计量是

可以验证当 Cov(θ̂opt,ŶDπ-ŶDπ+)→ 0 时，ŶDopt是YD的渐进无偏估计量。

利用独立样本追加设计还可以对总体的估计量进行改进，设C＝UD为剩余层，则剩余层YC=Y-YD的基于主体设计的目标变量的H－T估计量ŶCπ=Ŷπ-ŶDπ，可以得到终极设计下的总体总量 Y 的估计 Ŷbet(θ̂opt)=ŶCπ+Ŷopt，可以验证Y的H－T估计量和最优方差加权估计量 Ŷ(θ̂opt)都是无偏的。由此，构造总量Ŷπ的无偏估计类Ŷ ={Ŷ(α|θopt)= αYπ+(1- α)Ŷbet(θ̂opt),α ∈ R}，利用极小化方差V(α|θopt)求得最优点 αopt(θopt)，可得出

由此得到Ŷπ的最优估计量是 αoptYπ+(1-αopt)Ŷbet(θ̂opt)。

1.2 利用永久随机数进行的分层次抽样设计

上述样本追加方法都需要进行二次抽样，有时会导致样本单元的过量抽取和使用，利用永久随机数技术可以有效处理样本追加问题。永久随机数技术，即抽样框中的每个单元都被赋予从区间（0，1）产生的随机数，永久随机数和这个单元同时产生，同时改变，同时消亡。永久随机数技术实施起来非常方便，可以有效地解决多目标、分层次、与规模成比例的不等概抽样调查以及实现连续调查中的样本轮换等问题。将永久随机数技术和样本追加方法结合起来，可以有效地解决分层次调查中的样本兼容问题，方便的实现样本追加，使抽到的样本对总体有更好的代表性。抽样方法按照样本量是否固定分为两类，随机样本量和固定样本量的抽样方法。随机样本量的抽样方法有Poisson抽样、Bernoulli抽样、配置抽样、PoMix抽样和Mpps抽样，其中以Poisson抽样为代表。固定样本量的抽样方法有序贯Srswor抽样、序贯Poisson抽样、Pareto抽样和序贯PoMix抽样，其中以序贯Poisson抽样为代表。

利用永久随机数抽样技术可以方便地解决实际调查中存在的总体与层调查同时进行以及总体调查与层调查不同时进行的分层次抽样调查。

2 总体调查与各层调查同时进行

利用永久随机数法的分层次调查是对总体中每一个单位赋予永久随机数，确定样本的排列顺序，使各层次的样本能有较高的兼容共享性，也避免了二次抽样和样本重复抽样的情况。针对分层次调查中总体和层同时抽样的情况，即其中层与总体同时进行调查，此时只需对层进行调查，总体样本的数据也就能够从层中获得。此处我们利用永久随机数抽样法中随机样本量的Poisson抽样方法或固定样本量的序贯Poisson抽样方法来处理，因为Poisson抽样法是一种与规模成比例的不等概抽样方法，更符合实践中复杂抽样的设计。其中Poisson抽样法由于样本量的随机性，最终实现的样本量与期望的样本量有一定的差异，可以通过永久随机数的修匀来减少随机样本量的变动情况。下面介绍总体与层调查同时进行的两阶段分层次调查。

将总体的每一个单元赋予永久随机数，并将总体U划分为M个层，其中若干个层和总体同时进行估计，不失一般性，假设U1,U2,...Ur和U同时调查，总体的样本容量为n。

（1）当r=M时，即所有的层都与总体同时调查，利用永久随机数法，只需要对U1,U2,...Ur进行调查即可，因此首先在U1,U2,...Ur中分别利用永久随机数得到U1,U2,...Ur各自的样本，由永久随机数法的性质可知总体的样本一定在U1,U2,...Ur样本的并集中，此时只需在U1,U2,...Ur样本的并集中，按照总体样本的排列顺序选定前n个单元就可，因此无需再抽样就可以完成总体和各层的抽样。

（2）当r＜M 时，将U 划分为两个子集U(1)和U(2)，样本量分别为n1和n2。

在（2）中，若事先已知总体U 的两个子集U(1)和U(2)的样本量为n1和n2，则由永久随机数的性质，则两部分的样本之和即为总体中随机数最小的n个永久随机数对应的单元，为总体的样本。若事先不知道总体U的两个子集U(1)和U(2)的样本量为n1和n2，则首先按照（1）的方法在U(1)中选取永久随机数最小的n个单元作为总体U的样本，然后与U(2)中的单元的永久随机数进行比较，如果对应的永久随机数小于U(1)中的n个样本单元对应的永久随机数，则将Ui(2)迭代进入样本，将U(1)中的最大的那个随机数迭代出来，以此方式迭代下去，即得到总体U的n个样本单元。

多阶段的分层次抽样其方法是类似的，只考虑需要估计的层和其下的一个层次，视为两阶段的分层次抽样调查即可。

3 总体调查与层调查不同时进行

当总体调查与层调查不同时进行时，同样对总体中的每一个单元赋予永久随机数，具体实施思路如下，仍以两阶段的分层次调查为例。假设第一次对总体进行调查时此层的样本量为n1，由于此样本对于该层缺乏代表性，所以需要进行第二次抽样调查，即对该层进行样本追加，若追加的样本量为n2，利用永久随机数方法只需在选择n1个永久随机数对应的样本的基础上再选择n2最小永久随机数对应的样本单位即可，大于两层的多层次调查的方法类似。

4 利用永久随机数法的参数估计

通过上述分析，可以看到永久随机数方法有效地解决了各个层次的调查的样本兼容问题，很好地解决了多层次调查的样本的抽取问题，但是从抽样框中抽取样本不是抽样调查的目标，而是如何有效地对总体进行有一定精度的估计。

分层次抽样调查中的永久随机数抽样方法，一般是Poisson或序贯Poisson抽样方法。此处我们应用在Poisson抽样中利用广义回归估计量计算目标变量的无偏估计量，得到层的估计量是

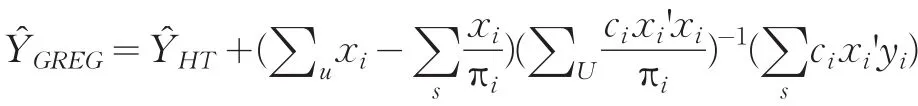
运用复杂方差的弃一的Jackknife方差估计方法，得到方法估计量

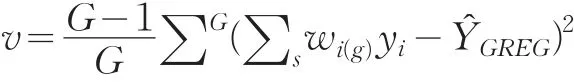
其中

随机组的划分是Jackknife方法的关键，随机组的具体划分要取决于调查的具体抽样设计。

5 总结

文章主要针对实际调查中的分层次调查问题展开讨论，现在许多大型的调查都需要在对总体的目标变量进行估计的基础对各个层次也进行有效的估计。本文主要介绍了冯世雍与秦怀振的样本追加方法和利用永久随机数的样本追加方法。

[1]秦怀振.抽样调查中若干理论与实践问题的研究[M].北京:中国统计出版社,2003.

[2]Rao,J.N.K.Small Area Estimation[M].New York:Wiley,2003.

[3]冯士雍.中国抽样调查应用中的若干问题[J].中国统计,2001，(11).

[4]林才生.分层次复合pps抽样设计[J].统计与决策,2006,(13)