含单调约束的广义回归估计量

杨贵军,吴洁琼

(天津财经大学 a.统计学院;b.中国经济统计研究中心,天津 300222)

一、引 言

广义回归估计量(Generalized Regression Estimator,GREG估计量)是在社会、经济和人口等领域的抽样调查中经常使用的一类估计量[1]。加拿大、英国等诸多国家的政府统计部门已广泛运用GREG估计量构建抽样调查估计体系,如加拿大劳动力调查(LFS)。关于GREG估计量的研究很多,但很少有文献在系统性应用GREG估计量时,考虑GREG估计量的假设条件。传统的GREG估计量假设域与域之间是相互独立的,忽略了域值间联系,如域总值、域均值等域特征值间的相关关系。更多的实际情况下,域值与域值间并非是独立的,调查变量的域值互为约束,随着域的变化呈特定的变化趋势。如全国工资统计抽样调查中分行业人均工资的估计,由一产农林牧渔业,到二产制造业、三产信息传输、计算及服务和软件业、金融业,行业内学历为本科及以上的人员占比、行业平均工资等变量随之呈递增趋势。在利用样本对总体估计时,忽视目标变量域值具有的特定趋势,将增大估计量方差,降低估计精度。Oliva等使用形状约束下的HT估计量估计美国高校毕业生的年平均收入,结果表明,较传统的HT估计量,形状约束下的HT估计量置信区间更小,精度更高[2]。

GREG估计量的研究主要围绕扩展GREG估计量应用场景和提高GREG估计量估计精度两个方面。Cassel等提出GREG估计量,并证明在辅助变量与目标变量线性回归方程过原点情况下,GREG估计量在所有设计线性无偏估计量中估计精度最高[3]。GREG估计量精度高、易构建,应用领域不断拓展。Estevao等归纳加拿大统计局的广义估计系统,提出应用于单阶段整群抽样、多阶段辅助抽样的GREG估计量[4]。陈光慧在总结加拿大等国家成功经验的基础上,尝试引进广义回归估计系统,并应用到中国连续多阶段抽样中[5]。然而对于GREG估计量,超总体模型设定不准确将降低GREG估计量的估计精度[6]。对此,众多学者尝试利用非参数回归模型建立目标变量和辅助变量间的关系模型,不需要对超总体模型设定。Breidt等分别基于局部多项式回归、样条回归、广义相加模型回归等构建超总体模型[7-9]。陈光慧和吴默妮通过借鉴局部多项式,对原始辅助变量信息进行扩展,得到原始辅助变量多次方形式的新辅助变量,基于新辅助变量提出广义最优回归估计量[10]。然而这些提高精度的方法都需要额外的调查信息,增大调查成本,部分信息甚至难以全部获取,使得估计方法很难广泛使用。本文拟借助辅助变量域值的排序信息构建含约束的GREG估计量,在既有的辅助信息域值已知的条件下提高估计量精度。

含单调约束的GREG估计量所借助的辅助变量需要满足其域值的变化趋势同目标变量域值的变化趋势一致的条件。该条件在农业调查、环境调查等大部分调查中都是易于满足的。一方面,在调查中辅助变量选取阶段,辅助变量同目标变量的相关关系是选取辅助变量的重要标准之一,辅助变量的增长速度和目标变量增长速度越一致,估计量的精度越高。因此,大多数抽样调查中,辅助变量的域特征值同目标变量的域特征值的变化趋势是一致的,如农业调查中利用养殖场(户)辅助估计牛羊禽的存栏量,随着养殖场(户)的增加,牛羊禽的存栏量增长。另一方面,随着大数据技术发展,辅助信息的来源愈加丰富,行政记录、互联网数据等各种类型的信息作为辅助信息被引入到抽样调查中。这为探寻到同目标变量域值变化趋势更加一致的辅助变量提供了现实基础,使得含单调约束的GREG估计量的应用前景更加广阔。

本文首先通过总结GREG估计量特点,在目标变量域值和辅助变量域值变化趋势一致情况下,利用GREG估计量的保序回归构建含单调约束的GREG估计量,并从理论上证明其优良性。其次,通过数值模拟的方法,在辅助变量域均值增长模型和超总体模型的各种组合下,分析比较含单调约束的GREG估计量和传统GREG估计量的估计效果,验证含单调约束的GREG估计量的应用优势。最后,使用中国健康与营养调查数据,演示含单调约束的GREG估计量的应用效果。

二、广义回归估计量

(1)

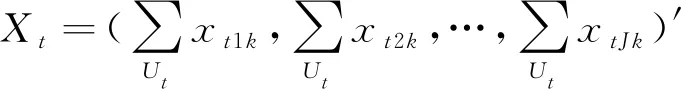
(2)

(3)

(4)

与经典的HT估计量相比,GREG估计量借助辅助信息对目标变量的估计量进行校准,估计精度更高。然而,GREG估计量忽略了域和域之间的相互联系,在域总值呈特定趋势情况下,估计结果存在背离目标变量趋势的可能,特别是在小样本下,估计量精度低。含单调约束的GREG估计量是在GREG估计量的保序回归基础上构建而成,能够在不增加调查信息的情况下,借助辅助域值排序信息,提高GREG估计量精度。结合GREG估计量的特点,在构建含单调约束的GREG估计量时需注意三点,一是含单调约束的GREG估计量所借助的辅助变量,其域值变化趋势同目标变量的域值变化趋势需一致。辅助变量和目标变量域值变化趋势的相关关系既可以由前期数据归纳得出,也可以由理论推导得出。同时,行政记录、互联网数据等资源的引入极大地丰富了辅助变量的来源,为获取域值变化趋势同目标变量一致的辅助变量提供了现实基础。二是含单调约束的GREG估计量所需的辅助变量信息同GREG估计量所需的辅助变量信息相同,均为样本单元的辅助变量信息和辅助变量的域特征值。含单调约束的GREG估计量借助辅助变量域值的排序信息作为约束条件,提高GREG估计量精度,无需额外调查信息。三是GREG估计量的估计精度与目标变量和辅助变量之间的相关性密切相关。应用含单调约束的GREG估计量,需要考虑目标变量与辅助变量的相关关系对估计量的影响。

三、含单调约束的广义回归估计量及其统计性质

本节拟在目标变量域值同辅助变量域值变化趋势一致情况下,通过借助辅助变量域值的变化趋势,构建含单调约束的GREG估计量,约束目标变量域值估计量的变化趋势。

(一)单调约束下的GREG估计量

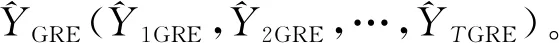
(5)

其中,域i的顺序不高于域t,域j的顺序不低于域t,si:j是域i到域j中所有的样本单元。

(6)

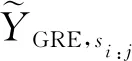
(7)

(8)

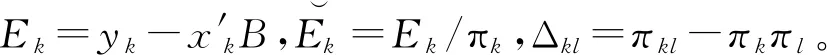
(9)

(二)含单调约束的GREG估计量的统计性质

借鉴史宁中和Wu对保序回归的研究方法,研究含单调约束的GREG估计量的性质[12-13]。首先需要以下的假设条件:

假设1:当N→∞时,Nt/N在[0,1]内,t=1,2,…,T;

假设3:GREG估计量协方差的极限满足00,

(10)

(11)

其中Σ是T×T维可逆矩阵,矩阵元素为Σtm。

假设1和假设2是总体中域数量和域均值的有界性假设。在大部分抽样中,例如中国农业抽样调查、全国人口调查等,假设1和假设2均成立。假设3、假设4和假设5是为确保估计量具有渐进无偏性的假设,在Fuller的研究中有类似的假设,对于HT估计量、GREG估计量等都成立[14]。根据以上几点假设,可以得出含单调约束的GREG估计量的以下性质:

(12)

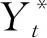
(13)

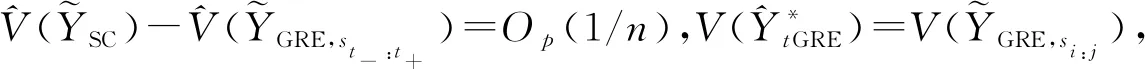
(14)

由此,有:

(15)

(16)

(17)

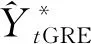
(三)含单调约束的GREG估计量的构建过程

第一步,依据外部信息,选择和目标变量域值变动趋势一致的辅助变量。获取辅助变量的域特征值以及样本单元的目标变量和辅助变量观察值。

第二步,针对总体内的每个域,利用样本单元观察值构建GREG估计量。第t个域第k个总体单元的目标变量观察值为ytk,辅助变量的观察值为xtk,则第t个域目标变量总值的GREG估计量为:

(18)

第四步,计算含单调约束的GREG估计量的方差估计量。利用样本残差,得到含单调约束的GREG估计量的方差估计为:

(19)

四、数值模拟

为验证含单调约束的GREG估计量的估计效果,采用模拟仿真的方法对GREG估计量和含单调约束的GREG估计量进行比较分析。

(一)模拟设计

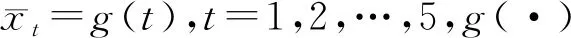
表1 辅助变量域均值的增长模型

表2 目标变量和辅助变量的回归关系模型

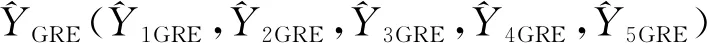
最后,分别计算不同域中GREG估计量和含单调约束的GREG估计量的评价指标:均方误差(MSE)、平均百分比绝对误差(MAPE)。MSE的计算公式为:

(20)

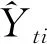
(21)

为评价方差估计量的有效性,分别计算GREG估计量和含单调约束的GREG估计量的方差估计量的均值(MV)及平均误差(ME)。MV的计算公式为:

(22)

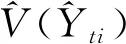
(23)

其中MSEt是第t个域的均方误差。

(二)模拟分析结果比较

表3 辅助变量域值和目标变量域值呈线性变化时和的比较

表4 辅助变量域值和目标变量域值的变化趋势呈二次函数时和的比较

表5 辅助变量域值和目标变量域值的变化趋势呈S型时和的比较

4.目标变量域值和辅助变量域值的变化趋势为COS型函数情况下的模拟结果。当目标变量域值和辅助变量域值的变化趋势为COS型函数时,目标变量域值随辅助变量域值先降低后增加,模拟结果由表6给出,表6的结构同表3。表6显示,含单调约束的GREG估计量在各类超总体模型下均优于GREG估计量。对于线性函数的超总体模型,含单调约束的GREG估计量和GREG估计量估计精度高,估计效果好。对于二次函数和三次函数的超总体模型设定出现偏误,GREG估计量和含单调约束的GREG估计量的精度降低,但含单调约束的GREG估计量精度降低得更慢。

表6 辅助变量域值和目标变量域值的变化趋势为COS型时和的比较

(三)小结

通过上述数值模拟分析,可以得出以下四点结论。在目标变量域值和辅助变量域值变动趋势一致的情况下,首先,含单调约束的GREG估计量在多种变动趋势下的估计精度均优于GREG估计量。该性质使其在农业调查、住户调查等使用GREG估计量的调查中具有广阔的应用空间。特别是随着大数据技术发展,行政记录、网络搜索记录等为估计量的构建提供了相关程度更高、更丰富的辅助信息来源,为含单调约束的GREG估计量的广泛应用提供了数据基础。其次,当超总体模型为线性函数时,含单调约束的GREG估计量和GREG估计量的估计效果趋于一致。再次,当超总体模型为非线性模型时,模型设定偏误将降低估计量精度,含单调约束的GREG估计量较GREG估计量精度更高,优势明显。但是,随着模型设定偏误的增加,含单调约束的GREG估计量的方差估计量精度有所降低,存在进一步的改进空间。最后,每个域中,含单调约束的GREG估计量的MSE降低的程度不同,当目标变量域值和辅助变量域值的变化趋势为一次函数,且超总体模型设定为三次函数时,含单调约束的GREG估计量在每个域的MSE降低的程度相近,且降低程度较多。在辅助变量域值的变化趋势为一次函数,超总体模型设定为三次函数情况下,含单调约束的GREG估计量最适用。

五、含单调约束的广义回归估计量在中国健康与营养调查中的应用

本文使用2009年度中国健康与营养调查(CHNS)来验证含单调约束的GREG估计量的统计性质。CHNS由国家营养与健康研究所和北卡罗莱纳大学的卡罗莱纳人口中心合作开展,旨在对中国社会经济状况、卫生服务、居民膳食结构和营养状况等内容进行观察和研究。本文选取总胆固醇水平作为目标变量,拟估计每个年龄阶段的平均胆固醇水平。由胆固醇相关研究可知,腰围异常和血脂异常的发生密切相关,腰围较同年龄腰围均值的偏离程度越大,高胆固醇血症患病的风险越大。腰围同胆固醇的变化趋势相近,因此可以借助腰围作为辅助变量估计胆固醇水平。目标变量和辅助变量的具体情况见表7。表7显示,随着年龄的增长,腰围均值和总胆固醇均值呈S型变化,同研究结论一致。

表7 各年龄段总体数据概况

以简单随机抽样方式从每个年龄阶段构成的域中抽取1%的样本,基于样本单元的胆固醇水平和腰围数据,以及各年龄阶段的平均腰围,分别计算每个年龄阶段的平均胆固醇水平的GREG估计量和含单调约束的GREG估计量,该过程重复1 000次。估计量的评价指标为均方误差MSE和平均百分比绝对误差MAPE。

表8给出GREG估计量及含单调约束的GREG估计量的估计效果。表8中第2列、第3列为GREG估计量的MSE和MAPE;第4列、第5列为含单调约束的GREG估计量的MSE和MAPE。表8显示,在估计偏差方面,含单调约束的GREG估计量的MAPE均小于GREG估计量的MAPE,含单调约束的GREG估计量相对偏差更小。在估计精度方面,含单调约束的GREG估计量的MSE均低于GREG估计量,含单调约束的GREG估计量的估计精度要优于GREG估计量。总之,尽管目标变量域均值的变动趋势和辅助变量域均值的变动趋势并不完全一致,含单调约束的GREG估计量仍较GREG估计量的估计精度更高。

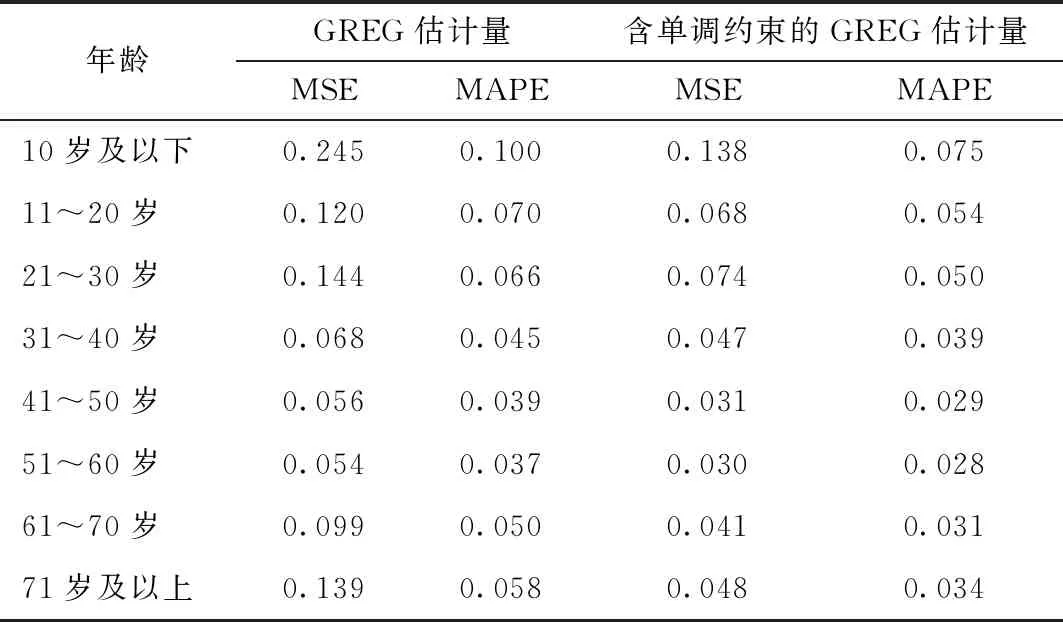
表8 平均总胆固醇估计结果

六、结 论

传统的GREG估计量对域值估计时要求域与域之间相互独立。忽视域与域之间的趋势,会出现估计值违背各域真实值趋势的情况,估计量精度低。对此,本文在目标变量域值和辅助变量域值变动趋势一致情况下,基于辅助变量域值,利用GREG估计量的保序回归,构建了含单调约束的GREG估计量。在目标变量域值和辅助变量域值的变化趋势近似情况下,含单调约束的GREG估计量的估计精度高于GREG估计量,偏差小于GREG估计量。

一方面,含单调约束的GREG估计量能够利用辅助变量域值顺序提高估计量精度,不需要获取额外的信息,估计精度高,调查成本低。特别是在超总体模型设定存在偏误的情况下,含单调约束的GREG估计量能够有效降低模型偏误对估计量造成的精度损失。另一方面,随着大数据技术发展,辅助信息的来源愈加丰富,比如覆盖范围广、数据准确度高的普查数据,高频率的行政记录,及时性更高的互联网搜索数据。丰富的辅助数据来源使得寻求同目标变量趋势一致的辅助变量更加便捷,也为含单调约束的GREG估计量的应用提供了现实基础,有利于社会、经济等领域抽样调查数据质量提高和成本降低。