受扰动长记忆随机场的BNLP回归估计

王 婧

(天津工业大学 数学科学学院，天津 300387)

在随机过程中，为了获得记忆参数来解释数据中的长征相依性，人们提出了很多方法来解决参数估计问题，尤其在一维时间序列和二维随机场的背景下讨论最多.然而，二维随机场的记忆参数估计问题由于其所具有的种种复杂性，其方法论发展远没有时间序列的方法论发展的快.

长记忆随机场的模型有很多种[1]，最常见的模型之一是各向异性的，即在不同方向上的记忆参数不相同.在各向异性随机场的记忆参数估计问题上，Boissy 等人[2]和 Guo 等人[3]研究了平稳各向异性随机场记忆参数的 Whittle 估计方法；Ghodsi 和 Shitan[4-5]讨论了分数求和可分离空间 ARMA (FISSARMA) 模型的对数周期图回归 (GPH) 估计量；Beran 等人[6]则采用了相同的模型，考虑了基于近似最小二乘的参数估计方法.这其中最经典的莫过于由一维时间序列推广到二维随机场得到的 GPH 估计方法，该方法最先是由 Geweke 和 Porter-Hudak 在无噪声扰动的时间序列参数估计中提出来的[7].

Ghodsi 和 Shitan 的工作[5]，虽然把 GPH 方法应用到了随机场中，但他们没有考虑噪声，也没有考虑估计量偏差的缩减.然而，在时间序列记忆参数估计的相关工作中，Sun 和 Phillips，以及 Arteche 在估计程序中加入了噪声项，对其扰动做出了响应[8-9]；Andrews 和 Guggenberger 则在 GPH 估计程序中增添了额外的回归项用以缩减估计量的偏差[10]，都在一定程度上提高了时间序列记忆参数估计的准确性.

因此，为了进一步拓展随机场中记忆参数估计方法的应用范围，并提升估计准确性，我们可以把时间序列中关于这两个方面的工作都扩展到随机场中.本文讨论把对数周期图估计方法应用到受噪声扰动的各向异性长记忆随机场的参数估计问题中，并采取在估计程序中增加回归项的方法来缩减估计量的偏差.

1 受扰动的各向异性长记忆随机场

本文考虑基于网格数据的受扰动的二维各向异性(弱)平稳(/齐次)随机场模型，其定义如下：

Yrs=μ+Xrs+Nrs,r,s∈

(1)

其中:μ是一个有限常数项，Xrs是在不同方向上显示出不同的强烈的反持久或长记忆的信号场，而Nrs则是一个噪声场，可以是一个白噪声过程，或是一个更一般的弱相依的平稳过程.另外，对于信号场Xrs，采用如下定义的完全可分的各向异性空间长记忆随机场模型[3, 5]：

Φ(B1,B2)(1-B1)d1(1-B2)d2Xrs=

Θ(B1,B2)εrs,

(2)

Φ(B1,B2)=Φ1(B1)Φ2(B2) Θ(B1,B2)=Θ1(B1)Θ2(B2)

(3)

其中:多项式Φi和Θi(i=1,2)的根在单位圆外，因此Xrs是平稳且可逆的，且其谱密度函数为

fX(λ1,λ2)=

(4)

其中:λ1，λ2∈[-π,π]对应的f*是一个标准可分空间ARMA模型的谱密度函数，定义如下：

(5)

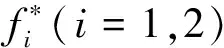
(6)

对于噪声场Nrs的谱密度函数，我们假设对于常数C0，L0>,有0≤fN(0,0)≤C0，且

(7)

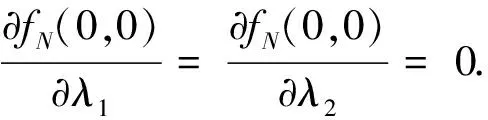
(8)

进而，当对于所有r,s∈，噪声Nrs与信号Xrs都不相关时，受扰动随机场Yrs的谱密度函数可以写为；

fY(λ1,λ2)=fX(λ1,λ2)+fN(λ1,λ2)

(9)

将式 (4)，(6) 和 (8) 代入式 (9)，可得

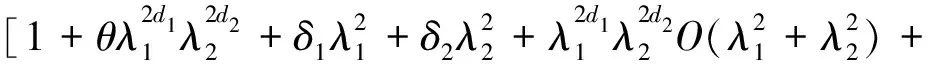
(10)

logfY(λ1,λ2)=logC-2d1log|1-e-iλ1|-

(11)

2 基于偏的缩减的非线性对数周期图回归估计量

假定我们是在规则网格Rn={1,…,n1}×{1,…,n2}上观测到了受扰动随机场Yrs的数据.那么，在提出估计量之前，先给出二位维情况下的周期图的计算公式如下所示[5]：

(12)

将式 (11) 中的fY(λ1,λ2)替换为在傅里叶频率λ1j,λ2k,j=1,…,m1,k=1,…,m2上计算的周期图坐标In(λ1j,λ2k)，做一些代数运算后可得

logIn(λ1j,λ2k)=a-2d1log|1-e-iλ1j|-

(13)

其中:a=logC-c，c=0.577 216……是Euler 常数，且Ujk=log(In(λ1j,λ2k)/fY(λ1j,λ2k))+c.据此，我们提出了如下的基于偏的缩减的多元非线性对数周期图回归 (BNLP) ：

logIn(λ1j,λ2k)=a-d1x1j-d2x2k+log[1+

(14)

(15)

这里d=(d1,d2)T，δ=(δ1,δ2)T目标函数

(16)

为了后续方便表达，将式 (16) 简化为

(17)

其中：

然后，对式 (17) 关于a进行浓缩，可得

(18)

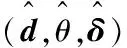
(19)

且

(20)

3 模拟仿真

本节对 BNLP 估计量在有限样本下的性能进行了仿真运算，并与 GPH 估计量进行了对比，考虑如下形式的受扰动长记忆随机场的模型：

Yrs=Xrs+Nrs

其中：信号部分的长记忆随机场Xrs采用平稳的完全可分长记忆 FISSAR(1,1) 模型[5,11]：

(1-φB1)(1-φB2)(1-B1)d1(1-B2)d2Xrs=εrs

(21)

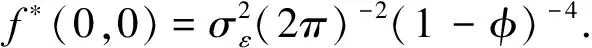
(22)

此外，本文采用非高斯噪声而不是高斯噪声，是因为我们认为 BNLP 估计量可以应用到受到任意噪声的随机场模型中，进而不需要加性噪声的高斯性的限制.

图1 当(d10,d20)=(0.4,0.2)，φ=0.2且 时长记忆信号场的仿真实现Figure 1 The realizations of long memory signal field with(d10,d20)=(0.4,0.2)，φ=0.2 and

图2 对数卡方的独立非高斯噪声场的仿真实现Figure 2 The realization of log chi-square, independent and non-Gaussian noise field

图3 当(d10,d20)=(0.4,0.2)，φ=0.2且噪信比为 5 时受扰动随机场的仿真实现Figure 3 The realization of perturbed random field with (d10,d20)=(0.4,0.2)，φ=0.2 and nsr=5

1)除去个别情况，GPH 估计量的偏差几乎全为负值，但 BNLP 估计量的偏差分布较为均匀，而且 GPH 估计量和 BNLP 估计量的偏差和 RMSE′s 会随着样本量的增多而减小.

2)噪信比对估计量的偏差存在负向影响，噪信比越大，GPH 估计量的负偏差就越严重，而 BNLP 估计量的正偏差则会逐渐减小，在部分情况下会导致负偏差.另外，随着噪信比的增大，两种估计量的 RMSE’s 总体上呈现上升的趋势，但 GPH 估计量的 RMSE’s 的上升速度要比 BNLP 估计量的快很多.

3)自回归系数增加对 GPH 估计量的偏差存在正向影响，对 RMSE’s 存在负向影响；而除去φ=0.8 的情况，自回归系数增加对 BNLP 估计量的偏差和 RMSE’s 存在负向影响.

4)在所考虑的 4 个带宽中，GPH估计量的偏差在m=[n0.5] 时达到最小值，RMSE’s 则在m=[n0.5]或[n0.6] 时达到最小值；而BNLP估计量的偏差达到最小值的带宽不稳定，但大部分情况下RMSE’s在m=[n0.8]时达到最小值，只有在φ=0.8且n=512时BNLP估计量的 RMSE’s在m=[n0.5]时达到最小值.但即使是在m=[n0.5]时，BNLP 估计量的部分情况下的偏差和 RMSE’s 会比 GPH估计量的偏差和 RMSE’s，在小样本n=128 时尤为明显.

表1 关于d0=(0.4,0.2)T在n=128时的估计量的偏差和RMSE′sTable 1 Biases and RMSE’s of d with d0=(0.4,0.2)T and n=128

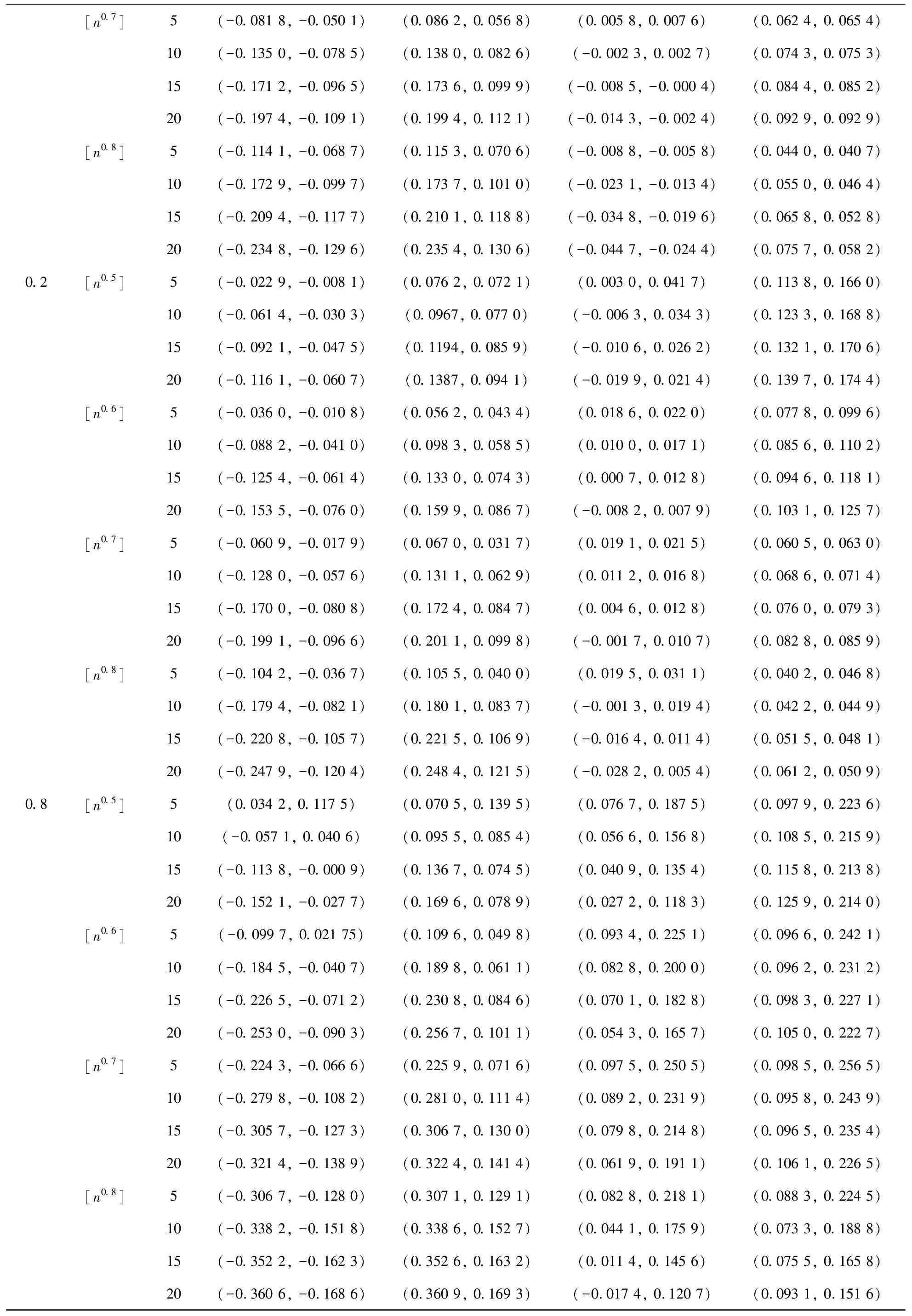
续表1

表2 关于d0=(0.4,0.2)T在n=512时的估计量的偏差和RMSE’sTable 2 Biases and RMSE’s of d with d0=(0.4,0.2)T and n=512

续表2

4 结 语

基于偏的缩减，并在明确考虑了噪声扰动项后，本文提出了半参数非线性对数周期图回归 (BNLP)估计量，来对完全可分的各向异性平稳长记忆随机场的记忆参数进行估计.经过数值模拟运算，结果表明，相较于 GPH 估计量来说，BNLP 估计量的偏差要较小些，而且即使噪声为非高斯噪声，BNLP 估计量也依然能够在强烈的噪声扰动下保持估计的稳定性，说明本文提出的 BNLP 估计量的优良性.

另外，数值模拟运算的结果还表明，BNLP 估计量在较高带宽时的表现要更好一些，在高噪信比的情况下也能保持稳定的估计效果，在数据量较少时也能较好地完成估计任务，而且 BNLP 估计量的偏差分布较为均匀，极大地改进了存在噪声扰动时 GPH 估计量严重的负偏现象，大大提升了记忆参数估计的准确性.

在之后的工作中，可以考虑更多类型的非高斯噪声扰动，来检验 BNLP 估计量的性能；并且可以采用其他优化方法，如 Nadarajah 和 Martin 的工作[12]，对估计量的偏差进行缩减，以达到更好的估计效果.