双重符合性审计抽样时的抽样规模的确定

耿修林

0 引言

运用抽样方法开展审计活动已有近百年的历史，经过这么多年的发展产生了许多样本审计测试的组织方式，它们大体上可区分为两大类别，即概率抽样和非概率抽样。非概率性质的审计抽样能充分融入审计的意图和审计人员的从业经验，但由此得到的样本测试结果原则上只能反映问题是否存在，不便于对审计对象总体情况做出符合数理逻辑的推断。纯概率意义上的审计抽样，虽然能保证由样本测试上升到对审计对象总体的反映，但在审计目的不很明确、审计人员业务经验不足时，一味依赖于随机规则实施抽样审计，有可能会产生较大的风险，甚至遗漏或不能找出问题所在[1]，这或许也是纯概率审计抽样测试在实际使用中时常遭受诟疑的原因之一。对此，如果采用试探性做法，先从审计对象总体中按概率方式抽取一个较大规模的样本，在初步检查掌握部分情况后再从这个较大规模的样本中抽取较小水平的测试样本，则可以弥补“直接抽样”的不足。这样的样本抽取方式，习惯上称之为双重抽样或双相抽样，其基本特征是从样本中再抽取样本[3]。

在相同的抽样规模和样本推断信度下，分层审计抽样的效果要好于简单随机审计抽样[3][4]。但在审计人员经验不足或不存在明显的分层标志情形下，要想取得良好的分层审计抽样估计效果也是不大有可能的。假如采用双重审计抽样，在获得第一重审计样本后，通过对第一重样本的直观观察和判断，然后再用分层抽样的办法，从第一重样本中抽取较小规模的第二重样本以此进行测试分析，就有可能会改善审计样本估计效果。

符合性审计也叫合规性审计，它主要检查审计对象总体错误发生的比例或被审计单位相关内控制度的执行情况等[2]。符合性审计中成数是其重要的估计内容，由于这种测试内容的特征，要是直接按照统计随机原则抽取测试样本可能在某些场合下行不通或者效果不好，原因是：符合性特征的发生带有某种程度的“稀少性”，可能在大量的审计单元中都不存在，这时先抽取一个比较大的第一重样本把那些真正具有审计测试意图的单位挑选出来再实施抽样，可能有助于快速确定出对测试具有价值的检查样本；通过双重抽样的第一重样本检查，能够获得有关辅助性资料，这对改善审计样本尤其是分层估计效果会有实质性帮助；纵使第二重样本单位检查的信息不能独立发挥作用，至少也可以对第一重样本审计检查的结果进行评估和调整[4]。

1 双重符合性抽样分层估计量的精度

为便于讨论双重符合性审计抽样时的抽样规模，在此先对双重符合性抽样分层估计原理进行简要的说明。假定从审计对象总体中按照纯随机抽样方法抽取容量为n′的第一重样本，然后将其分成L层，其中第h层的第一重样本单位数为 n′h(h=1,2,...,L)，n′=n′1+n′2+...+n′L。从第一重样本中抽取容量为n的第二重样本，属于第二重样本第h层的样本单位数为nh，那么n=n1+n2+...+nL。用表示由第一重抽样得到的第h层层权，总体的第h层真实层权用Wh=N′h(N′)-1表示，N′为总体全部单位数，N′h为总体第h层单位数目。Yhj为第h层第 j个总体单位测量，且取值0或者1，yhj表示第h层第 j个样本单位测量，同为0-1变量。在这些符号的约定下，容易得到审计对象总体符合性成数P=WhPh的样本估计量，因为第一重样本的层成数 p′h为

第一重样本成数p′

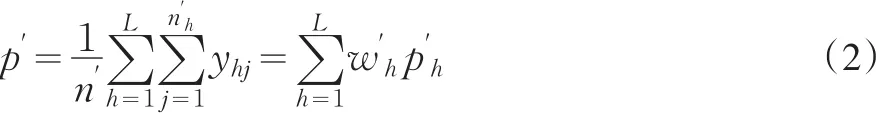
第二重样本第h层的样本成数

它可用作第一重样本层成数 p′h的估计，并且还是无偏的估计量[4]。此时，总体符合性成数P的估计量可以构造成

其中，pstd表示双重分层抽样时的样本符合性成数。

在抽样测试水平比较大时，理论上可以说明pstd是总体均值P的无偏估计，用 pstd估计总体符合性成数P的方差为

在第一重抽样比和第二重抽样比较小的情形下，式（5）可简单表示成

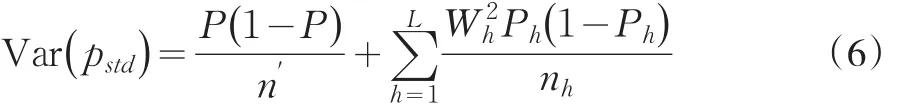
2 双重符合性审计抽样分层推断时的抽样规模

对双重符合性审计抽样测试问题，一方面需要给出第二重抽样水平的计算办法，另一方面也要确定出第一重抽样测试的样本检查规模。依据决策分析的原理，大致有两种处理方法，即“常规决策”分析和贝叶斯决策规则。

2.1 “常规决策”分析

样本估计精度大小与样本推断风险之间存在一定的联系，“常规决策”分析是根据事先给定的费用预算约束，尽可能地提高抽样估计精度即最大限度地降低估计量的方差，然后以此来确定抽样测试水平。

双重抽样测试的费用由两部分组成，一部分是抽取第一重测试样本发生的费用，另一部分是抽取第二重测试样本的费用[3]。设第一重测试样本每个单位的可变测试费用为c1，这样第一重抽样总的可变检查费用c1n′。由于第二重样本是符合性审计抽样测试的关键部分，有关这一部分的检查费用需要给出更为详细的说明，假定第二重测试样本中每个层的样本单位检查的可变费用为c2h，这样为简单起见分层用双重审计抽样测试的全部可变费用可采用如下的线性函数进行描述

其中的C表示测试检查的全部可变费用支出。

根据一般的抽样调查原理，由于第二重测试样本每个层中分配的样本单位数是随机变量，为此需要考虑在固定第二重抽样各层抽样比的基础上，计算审计样本测试全部可变费用支出的数学期望

其中，γh为既定的第二重测试样本的层抽样比。

估计量 pstd的方差由式（5）给出，在引进第二重测试样本固定的层抽样比情况下，可以将式（5）改写成

对其进行变形处理

把式（8）与式（10）相乘得

根据CAUCHY-SCHWARZ不等式得

由此可解得第二重符合性审计抽样中各层的抽样比

把式（13）代入到式（7），得到第一重抽样的最小抽样测试水平，即

在第一重抽样规模给定时，可以得到

如上所述，第二重样本量是随机变量，对其求数学期望可以给出双重符合性测试抽样时第二重抽样的平均抽样水平

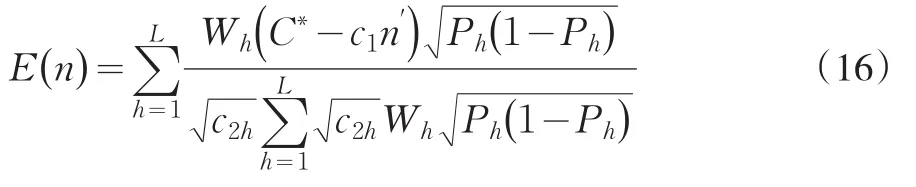
对双重符合性测试抽样在第二重抽样时层间样本量采用等比例分配，此时式（6）可简洁表示成

此时，假定检查可变费用采用函数

1.2.1 实验组教学方法 Mini-CEX考核评估项目包括7种：病史采集；体格检查；医德医风；医患交流；临床诊断；治疗方案；整体评价。实施步骤：（1）设计以Mini-CEX考核内容为基础的内科护理学授课计划及内容，并在教案中体现。（2）教师布置病例，要求护生结合病例进行角色扮演，内容包括病史采集、体格检查、临床诊断、治疗方案，其间要体现医德医风、医患交流。（3）每次课程最后20分钟，教师抽取1名护生以Mini-CEX考核表格进行全面考核，当场进行评价并反馈。Mini-CEX的优点是护生可以及时获得反馈，在给一名护生进行反馈的同时，其他护生也有收获。

那么，关于双重审计抽样的抽样规模确定，还可以有个稍微简单一点的计算方法。

联合式（17）和式（18），构造如下的符合性抽样规模决策分析数学规划模型

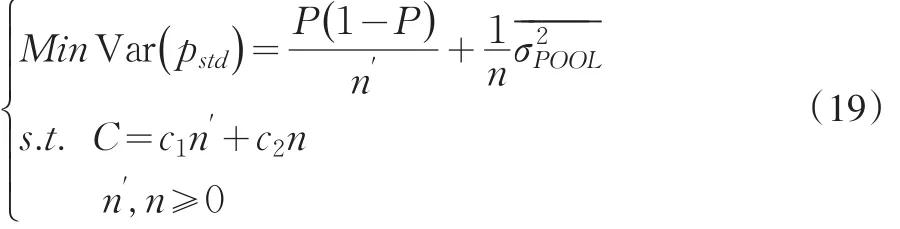
把约束规划转换成无约束问题，利用拉格朗日法则能得到

通过求极值，得到

对测试费用给定，把式（21）代入式（18）

由此解出的第一重符合性抽样测试规模的计算公式

反过来，把式（23）代入到式（18），能得到第二重符合性抽样测试水平的计算公式

2.2 贝叶斯决策规则

运用“常规决策”分析法确定符合性审计抽样测试水平的“缺陷”是，它直接把样本估计精度和抽样测试费用这两类性质不同的东西放在一起处理，虽然最终能给出分析的结果，但从事理上有说不通的嫌疑。贝叶斯决策规则在确定符合性审计抽样测试规模的时候，不仅把样本估计精度与由此衍生出来的判断失误风险损失有机地结合起来，同时还兼顾了审计样本测试发生的费用[5]。因此，贝叶斯决策规则对审计抽样测试的损失或费用运用得更为深刻，也更符合客观现实的逻辑。

假定由样本测试资料做出审计判断失误的损失可以用价值量来刻画；由样本测试资料进行审计判断的失误可以用总体符合性成数估计的误差来反映。那么，根据贝叶斯决策的基本做法，可以构造如下形式的双重符合性审计抽样规模确定模型：

在第二重审计测试抽样层间样本数目采用等比例分配的假定下，式（25）等价于

通过求解无条件极值可得到

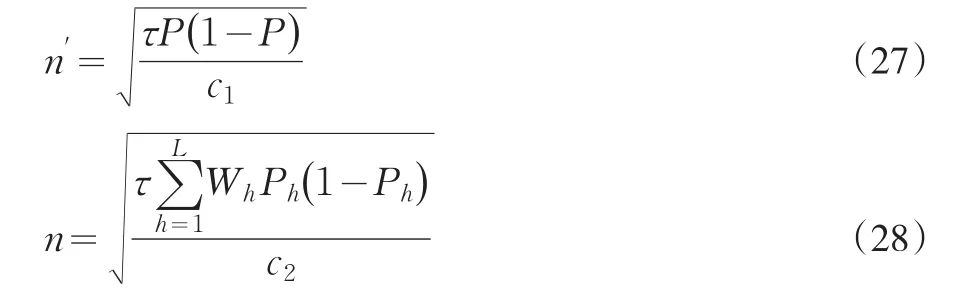
3 结论

样本测试规模的大小对审计样本测试推断结果的影响是客观存在的。按照概率统计的一般原理，样本测试规模过小，有可能会产生更大的样本估计风险；反过来样本测试规模较大，由此会在一定程度上提高估计精度，相应地也就能降低样本推断风险。但测试样本也不可能无限增大，否则就达不到抽样审计的目的。另外，既然是抽样审计样本测试组织方式可以针对特定对象的特征进行安排，但样本测试的规模需要结合样本推断要求以及测试费用约束来加以确定。这一方面是为了增加工作的规范性；另一方面是为了减小审计责任和风险。

[1]李凤鸣.审计学原理（第5版）[M].上海:复旦大学出版社,2011.

[2]毛节飞.审计理论与实务[M].北京:经济科学出版社,2009.

[3]冯士雍,倪加勋,邹国华.抽样调查理论与方法[M].北京:中国统计出版社,1998.

[4][美]W.G.科克伦.抽样技术[M].张尧庭,吴辉译.北京:中国统计出版社,1985.

[5]Hans Peter Stuger.Asymmetric Loss Functionsand Sample Size Deter⁃mination:A Bayesian Approach[J].Austrlan Journal of Statistics,2006,(35).