多种检测目标下样本容量设计的比较
罗 森,李 立,安 伟
(1.北京林业大学 经济管理学院,北京 100083;2.中国检验检疫科学研究院,北京 100123;3.中国科学院 生态环境研究中心,北京 100085)
0 引言
抽样检验是指根据概率论与数理统计原理,从一批产品中随机抽取少量产品作为样本进行检验,据以判断该批产品合格与不合格的检验过程[1]。由于产品数量和成本等方面的原因,对一批产品进行质量判定时很难进行全数检验,产品质量检验的结果很大程度上由抽取的样本所决定[2]。而抽样进行过程中,样本容量的确定是一个重要的问题。理论上,样本容量越大,代表总体越充分,调查精度越高[3],但如果样本容量过大,不仅会造成不必要的人力、物力、财力的浪费,加大调查成本,也会降低实施抽样的可操作性;如果样本容量过小,可能会因样本缺乏代表性造成抽样误差增大,抽样调查结果的可靠性将难以保障[4-7]。特别是在食品安全监控过程中,随着检测的化学物质的增加,监测的目标也随之扩大,各监测目标就对应着不同的最优样本容量。因此,合适的样本容量计算方法对于多种检测目标下的抽样调查非常重要[3]。
概率论中的大数定律和中心极限定理为抽样调查中样本容量的确定奠定了理论基础[8]。在简单随机抽样的条件下,已知总体方差或总体成数并给定极限误差和置信度的情况下,就可以计算出相应的样本容量。欧盟委员会的农药残留监控体系中的抽样数量计算方法,则以n重伯努利试验为理论基础[9],该方法在已知总体不合格率并给定置信度的情况下,也可计算出相应的样本容量。然而两种方法在使用上存在很大差异,在同样的不合格率和给定的置信度下却计算出迥异的结果。
本文将在对比上述两种方法的基本原理基础上,根据监测数据,采用这两种方法分别进行样本容量计算,对结果进行分析比较,并据此讨论根据不同的调查目标选择最优样本容量计算方法。
1 两种样本容量计算方法的比较
1.1 方法1
在简单随机重复抽样的条件下,根据区间估计的相关知识,假设总体成数为P,样本成数为p,则样本成数的标准差为
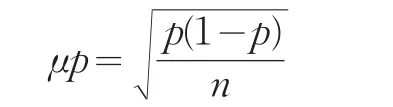
只要n充分大,一般np>>5和n(1-p)>>5时[10],根据中心极限定理,p近似服从正态分布N~(p,p(1-p)/n)。因此,构建标准化统计量Z

可知,在重复抽样条件下,已知总体成数为P,给定抽样极限误差及概率保证程度,则至少应该抽取的样本容量为
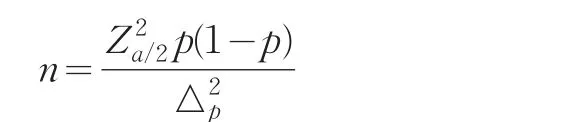
其中,n表示样本单位数;Δp表示抽样极限误差(最大允许误差);Zα/2表示在显著水平为α时,标准正态分布在α/2处的临界值。这里需要注意的是,计算结果需要向上取整。
从公式我们不难看出,影响样本容量大小的两个主要因素是极限误差Δp和统计量Zα/2,而统计量Zα/2又由显著性水平α和置信度来决定。极限误差越小,样本容量就越大;置信度水平越高,样本容量就越大[3-6,11,12]。
1.2 方法2
根据n重伯努利试验和二项分布的有关知识,若n次取样中每次取到的不合格品的概率为p,则至少检测出一个不合格样品的概率为

欧盟委员会2002/63/EC指令欧盟农药残留监控体系中规定,为确保样本在所检查的货物/商品中具有典型性,取样须按照委员会指令2002/63/EC(EC,2002)确立的农药残留官方控制方法进行,按公式
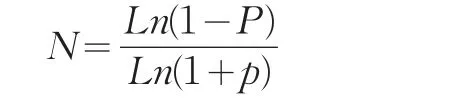
计算确定抽样样本容量[13]。
2 两种方法的比较实证
我们给定总体的不合格率,并分别设定置信度为90%、95%、99%,方法1的允许误差为5%,运用方法1和方法2分别计算相应的样本容量,结果如表1。
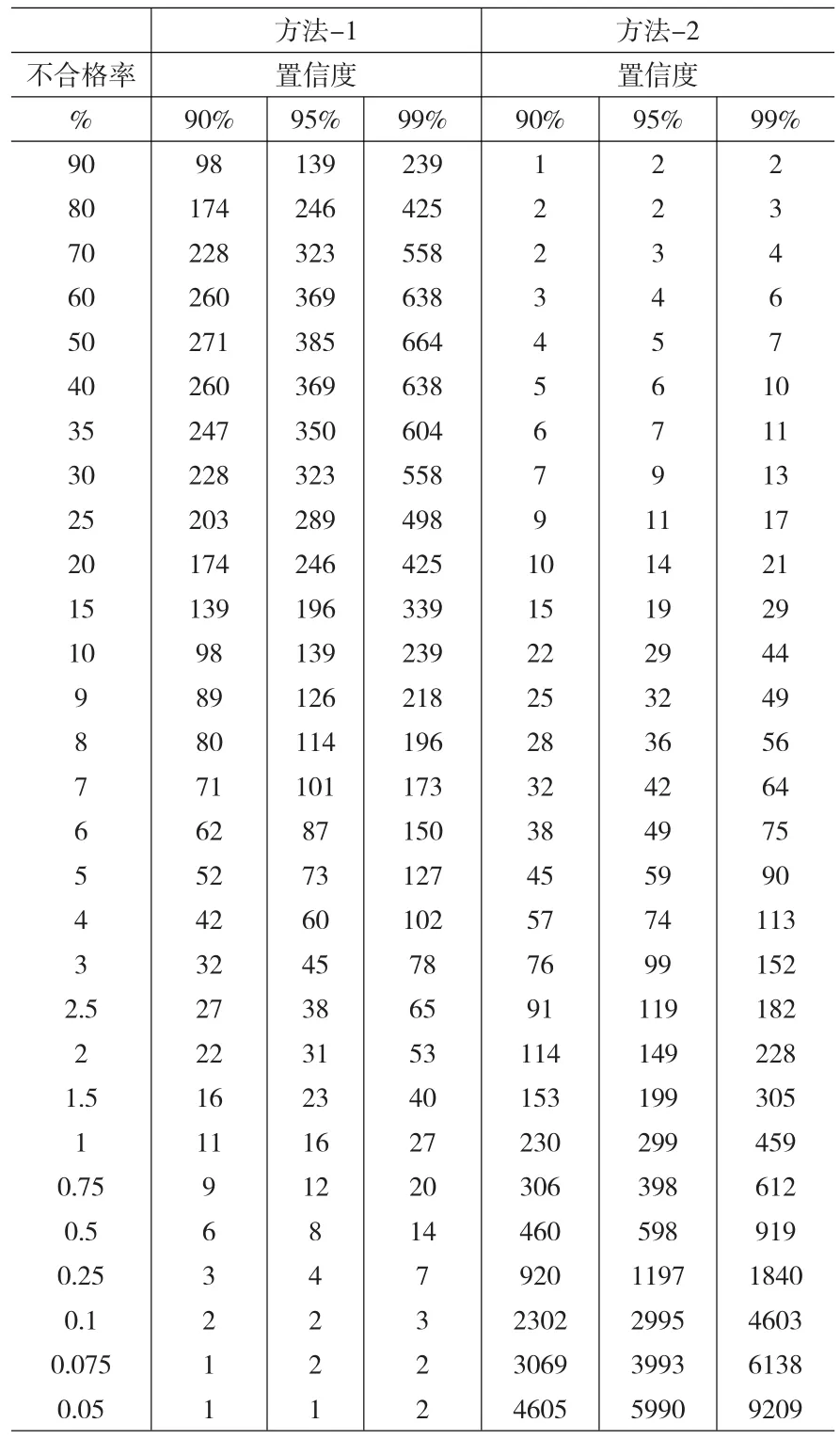
表1 不同参数下两种方法的样本容量计算结果
表1给出了两种方法计算出的样本容量在各个不同置信度下随不合格率变化而变化的结果。方法1的计算结果趋近于正态分布,样本容量极大值出现在不合格率为50%处。方法2计算的样本容量随着不合格率的下降而逐渐增加,尤其是在不合格率小于1后出现陡增。在同样的置信度下,随着不合格率的增加,两种方法计算的样本容量有着明显的差异。分别抽取表1中两种方法在95%置信度下计算出的样本容量数,如图1。
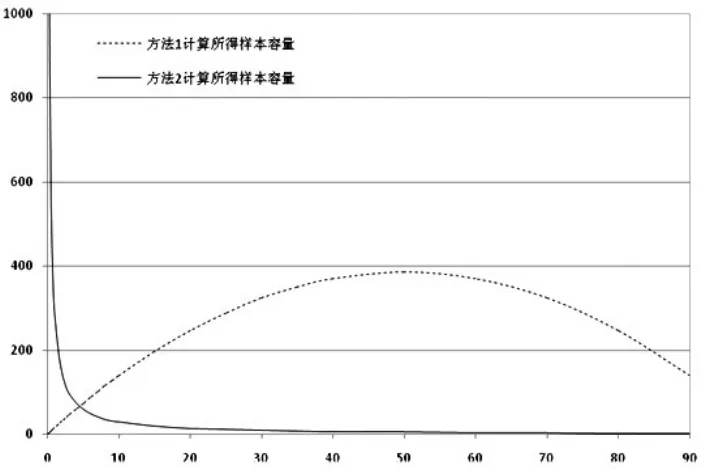
图1 不同合格率95%置信度下两种方法计算所得样本容量
两种方法最大的不同是方法1中存在极限误差[14],极限误差是对抽样估计的误差范围提出的要求,其确定一般需要具体问题具体分析,需要根据经验或试验分析后给出[15]。当实际超标率很低时,我们通常认为其合格;反之,实际超标率很高时,通常认为不合格。因此,当检出率为50%时,我们很难判断其是否合格,此时判断合格的不确定性最高。方法1由于要求调查的目标结果在允许的误差范围内,所允许的误差越小,则需要的样本容量越大;方法2的应用目的在于“至少检测出一个不合格样品”,也就是说检出即是不合格,所以方法2中的不合格率应指的是实际检测中的超标率。如表1,随着超标率的降低,则检出至少一个不合格品所需要的样本容量也就越大。
以上分析可以看出,两种方法计算出的样本容量大小有明显区别,也存在着不同的适用条件。方法1对应着检出率和容许的误差精度,更适用于我国出口食品质量监测。目前发达国家为了控制食品安全,在进出口食品贸易中设置许多技术贸易壁垒[16],因此我们有必要在出口食品检测中严格把关,针对出口国设置的技术贸易壁垒有效控制我国出口食品的质量安全,防患于未然,避免遭受不必要的经济损失。方法2对应着超限率,更适用于我国进口食品质量监测。在同一批次样品中只需检出一个不合格品即可拒绝整批货物,用方法2可以使我们在抽取很少样本的情况下达到监测进口食品安全的目的,将大大提高管理效率。

表2 按各样品检测项目检出率和超限率计算所得样本容量
为了对上述两种方法所计算的结果有更加直观的认识,这里根据地方管理部门对部分进出口样品农药和重金属的监测数据,计算相应的样本容量,如表2。
由表2可以看出,多种目标下每一个检测项目的检出率和超限率都会对应得出一个样本量,在保证最高置信度的条件下采取取大原则[15],即将抽样调查的样本容量确定为所有样本容量需要值中的最大值,这样做可以满足所有指标对抽样误差的要求。将表2数据根据取大原则进行处理,如表3。
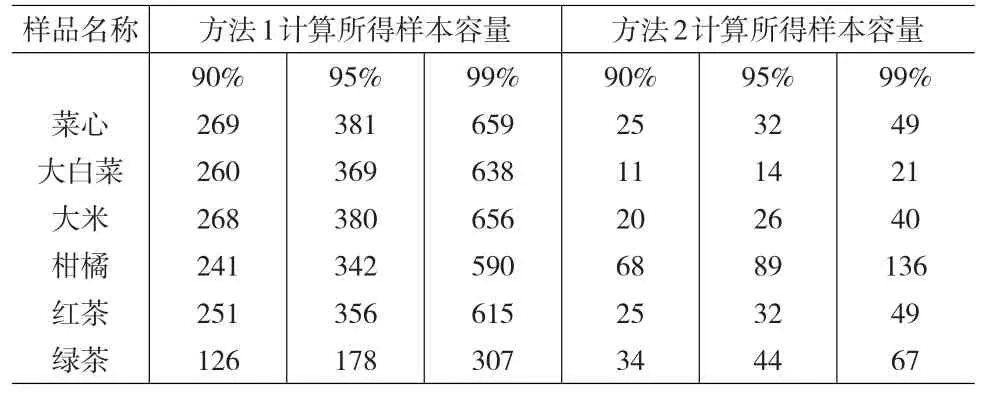
表3 各样品在不同置信区间下最终应取样本容量
以表3中菜心为例,通常,95%置信度下,如果一批菜心需要出口,则该批次的菜心应该抽取381个样本进行检验;如果一批菜心需要进口,则该批次的菜心应抽取32个样本进行检验。
3 结论
我们分析了两种样本容量计算方法的原理,并采用进出口食品的农药和重金属监测为目标案例计算了进出口食品的样本容量。但这两种方法并不能解决所有的问题。比如,以往的监测数据显示该样品的所有检查目标检出率为0%或100%,则这两种方法都不能计算出应该抽取的样本容量,这种情况样本容量如何确定仍待进一步研究和讨论。另外,本文所讨论的两种方法是在小范围内实施的样本容量确定方法,如何将这些方法合理的运用到不同层次的抽样监测当中,也是仍需研究的问题。
[1]刘苗苗,宁尚勇,云振宇等.我国乳制品抽样方法及标准现状分析[J].农产品加工(学刊),2010,(3).
[2]卢凤华.产品质量检验抽样方法研究[J].科技致富向导,2011,(21).
[3]贺建风,刘建平.多指标抽样的样本容量设计方法[J].统计与决策,2008,(17).
[4]纪利霞.抽样调查中样本容量设计[J].山西大同大学学报(自然科学版),2009,(3).
[5]李良.抽样调查中样本容量的计算[J].科技经济市场,2009,(9).
[6]李鹏祥.随机抽样中必要样本容量的确定[J].赤峰学院学报(自然科学版),2009,(9).
[7]刘爱芹.随机抽样中样本容量确定的影响因素分析[J].山东财政学院学报,2006,(5).
[8]张国友.关于抽样调查中样本容量的确定[J].安徽理工大学学报(社会科学版),2003,(1).
[9]茆诗松,程依明,濮晓龙编著.概率论与数理统计教程[M].北京:高等教育出版社,2011.
[10]陈在余,陶应虎编著.统计学原理与实务[M].北京:清华大学出版社,2009.
[11]薛长青.浅谈影响样本容量大小的因素和对调查误差的认识[J].工业技术经济,2001,(4).
[12]李永娣.统计推断中样本容量的确定问题[J].河南省情与统计,2000,(8).
[13]Commission E,Others.Commission Directive 2002/63/EC of 11 July 2002 Establishing Community Methods of Sampling for the Official Control of Pesticide Residues in and on Products of Plant and Ani⁃mal Crigin and Repealing Directive 79/700/EEC[Z].EEC,2002.
[14]WilliamMendenhall美,TerrySincich著美,梁冯珍4等.统计学[M].北京:机械工业出版社,2009.
[15]陈克明,宁震霖.市场调查中样本容量的确定[J].中国统计,2005,(3).
[16]聂雪梅,储晓刚,李立等.进出口食品安全问题、趋势及改善初探[J].食品科技,2010,(1).

