速率理论中分子扩散项的置换模拟与经济学思考

游士兵，苏正华，崔娅雯，杨艺芳，陈蔚妮

（武汉大学经济与管理学院，武汉 430072）

0 引言

本文是在色谱经济分析法置换系列研究：塔板理论置换研究（游士兵等，2011-2012）的基础上的后续研究，塔板理论在色谱分析法中所具有的重要地位和作用已经在先前的研究中进行了详细的叙述（游士兵，2011），本文不再赘述。但是，作为一种半经验理论，塔板理论还存在许多的不足：

第一，一种物质溶解在某种溶剂中，要达到分配平衡总是需要一定的时间，不可能瞬间完成，因此塔板理论关于组分在柱内运动时，能够在固定相和流动相之间快速实现平衡的假设是难以实现的。在经济领域中，部分消费者在进行消费时并不瞬间做出消费决定，总是要经过对比思考才会做出消费选择，从而使决策的时间延长，使得塔板理论不能较好地描述经济活动；

第二，当一种气体混入到另一种气体中时，气体分子总会受热运动的影响而从高浓度区向低浓度区扩散，因此溶质在载气中运行时总是存在纵向扩散，而塔板理论忽略了由于浓度差所引起的组分在色谱柱中的纵向扩散，特别是当传质速度很快时，其纵向扩散作用为主导方面。同样，由于受到多种经济因素影响以及经济主体之间的相互影响，部分经济主体在消费区域中处于观望状态，总是先流向人数较少的消费空间内进行考察，避过消费高峰期之后才开始进行消费选择，这种扩散作用就使得分离组分时的流出时间延长；

第三，塔板理论未能说明决定塔板高度H的参变量，未能回答H是如何影响色谱峰扩张等一些实质性的问题，并且未能解释流动相线速度u不同时，柱效能n不同的原因，以及当u值由很小一下子变得很大时，n指标并未变化许多、但是峰宽各异的原因。同样，经济领域中的经济增长速度、市场对消费者的消费吸引力等因素，都会影响单位柱长的总偏差，进而使塔板高度H受到影响，塔板理论也不能描述这种影响。

这些不足的存在，反映了塔板理论并不能较为全面地说明色谱流出曲线各种行为的内在原因。为此，作为对塔板理论的修正，1956年，荷兰人Van Deemter以及后来的研究者在吸收塔板理论概念的基础上，将影响塔板高度的动力学因素结合起来，提出了色谱过程的动力学理论——速率理论。为此，经济学如何进行速率理论的分析，是我们的研究主题。

1 速率理论的基本原理

1.1 Van Deemter方程式的理论模型

被分析物质谱带在柱里运动过程中，实际上不可能在流动相与固定相间瞬时达到平衡，意味着组分分子在两相中交换时，其传质速度并非无限大，真的实现组分分配平衡需要花费一定的时间才能达到。随机行走理论模型对组分分子在色谱柱中的分离移动规律进行了这样的描述：组分气态分子由载气携带纵向前进，而固定液分子却拉着它不许前进，但因为载气是连续不断地向柱出口处冲洗，固定液分子就会逐渐释放组分分子，由于各组分在固定相中的溶解度不同，其在柱中的滞留时间就不同，从而运行速度不同，同时，组分分子运动中还会受到载气阻力、气相浓差扩散及传质阻力等影响，使之达到柱终端时间延缓，造成谱峰扩张。也就是说，组分只能在一维空间或在直线上按照随机过程行走，不同的柱过程都有其一定的平均步长l，组分分子在柱中共走了Nl步。对一个分子而言，行走N步，每步步长为l，则一定时间后它会距原点相当距离；多个分子如此随机行走，由于Nl和l不同，在经过一定时间后，它们离原点便会呈现一个分布，这种距离偏差，可以用正态分布的标准偏差σ表示：

称σ2为变度，如果将式（1）引申到各个随机过程，则色谱峰的总偏差等于各独立影响因素偏差之和，即

根据随机行走模型的探测，可知色谱分离过程中的柱效率的独立影响因素为涡流扩散、分子扩散、气相传质及液相传质阻力，但实际上，决定柱效的是单位柱长的总偏差（σ2/L），而不是各独立因素项的偏差。

所以，此时色谱柱的总板高就等于各独立影响因素对板高贡献的和：

可能有两个因素相互影响，对H产生交界贡献或耦合贡献，但该式应看作是随机理论模型的基本解释式。

1.2 Van Deemter方程式

1956年荷兰学者van Deemter（范第姆特）等在研究气液色谱时，提出了色谱过程动力学理论——速率理论。他们吸收了塔板理论中板高的概念，并充分考虑了组分在两相间的扩散和传质过程，从而在动力学基础上较好地解释了影响板高的各种因素，该理论模型对气相、液相色谱都适用。速率理论方程主要讨论组分在色谱柱内几种传质过程所引起理论塔板高度（H）增加（即柱效能n降低），从而导致峰展宽，使柱选择性、分离度等变差。该方程可以用来指导实际的色谱操作过程，选择色谱系统的最佳操作参数，使Van Deemter方程中诸因素向降低理论塔板高度方面转化，以保证获得良好的柱效和理想的色谱峰。Van Deemter方程的数学简化式为：

H=A+B/u+Cu

式中u为流动相的线速度，A、B、C为常数，分别代表涡流扩散系数、分子扩散项系数、传质阻力项系数。其中，分子扩散又叫纵向扩散项，是以浓度差为动力的，分子沿色谱柱中流动相的正向和逆向扩散，流动相流速越大，逆向的扩散就能很好的得到控制，固定相的吸附能力越强，分子扩散项就越小。本文以分子扩散项B作为置换对象进行讨论，涡流扩散项和分子扩散项的置换将另文研究。

2 分子扩散项（B）及其置换思考

2.1 分子扩散项（B/u）

在色谱柱中，当样品以“塞子”状态注入色谱柱后，由于组分分子只占柱中的很小一部分，并不能充满整个色谱柱，那么在色谱柱方向上就会形成一定的浓度梯度，当组分随流动相流动时，向前运动着的分子就会产生浓度之差的扩散作用（由高浓度向前进方向的低浓度扩散），并且是沿着轴向而加速，从而引起峰展宽，故称此为纵向扩散或轴向扩散。

在组分运动的过程中，组分分子扩散与组分在气相中的停留时间（tM）成正比，所以分子扩散所引起的距离偏差为：σ2=2DgtM，其中，Dg为气相扩散系数，tM为载气在柱中的停留时间，即为组分在气相中停留的时间，tM与柱长和流动相的线速度u有关，即tM=L/u，则有σ2=2DgL/u，也就是说，分子扩散项与u值成反比，流动相的线速度u越小，柱越长，组分在柱中的停留时间tM越长，纵向分子扩散作用就越加剧。在色谱柱中，由于气相流路具有很大的弯曲性，所以必须对载气线速度u加以校正，即引入弯曲校正因子γ值，γ反映了固定相颗粒的几何形状阻碍分子扩散的程度，一般小于1，组分在气相中的停留时间tM=L/(u/γ)=Lγ/u，由分子扩散项引起的单位柱长的距离偏差为：

由上式可以看出，分子扩散所引起的色谱区带宽度扩张与溶质停留时间和扩散系数成正比，板高与分子纵向扩散系数成正比，与流动相的线速度成反比。B与弯曲因子γ和扩散系数Dg有关，弯曲因子γ跟色谱柱内固定相的填充情况有关，表示由于柱中的载体存在，阻碍组分分子不能自由扩散而使扩散距离下降，故用γ几何因子校正。γ值通常小于1，在硅藻土类载体中γ值在0.5～0.7之间，它反映了填充物的空间结构，在毛细管中因无填充物的扩散阻碍，所以γ=1。扩散系数Dg是固定不变的，它与组分的性质、载气的性质、柱温柱压力有关。组分分子质量大，则Dg值小；Dg又与载气分子质量M的平方根成反比，即，所以用分子质量大的载气可以降低B值。Dg随Tc增加而增加，但随pc增加而下降，通常Dg为0.01～1cm2/s。

因此，在实际操作的过程中，如果加快载气的流速，就可以减少由于分子扩散而产生的色谱峰扩张。由于组分在气相中的扩散系数Dg近似地与载气的摩尔质量的平方根成反比，所以实际过程中使用摩尔质量大的载气可以减少分子扩散。同时，选择球状颗粒和相对分子质量较大的物质作流动相，并适当地增加流动相的线速度，采用柱长较短的色谱柱和较低的柱温，都可以减少纵向分子的扩散。

2.2 分子扩散项的置换思考

一般来讲，在色谱柱内的固定相和流动相都会存在分子扩散，由于固定相静止不动，因此固定相中的分子扩散可以忽略，本文所论述的分子扩散项只考虑气相色谱流动相中的组分分子扩散。

2.2.1 分子扩散项

样品在进入色谱柱后不能立即充满整个色谱柱（也就是分配不均匀），使得组分分子存在浓度梯差，浓度梯差又引起组分分子的纵向扩散，这就是分子扩散项的来源。可见，分子扩散是由色谱柱方向组分所存在的浓度差造成的；从分子扩散项的表达公式来看，影响分子扩散的因素主要有弯曲因子γ、扩散系数Dg、载气的线速度u，γ的取值范围通常为γ≤1。那么，我们就要结合所研究的经济现象对相关的因素进行对应置换。

我们通常所说的浓度，是以单位体积中所含溶质的物质的量来表示溶液组成的物理量，浓度差是不同溶液中所含溶质的物理量的差异，它与组分自身的内在本质属性没有必然联系。在化学色谱分析中，浓度差产生的原因是载气速度或者说流动相的速度不够快，如果载气速度够快，样本在柱中的分布就会比较均匀，浓度差就相对较小。在此前对塔板理论进行置换时，载气被认为某种促使消费者在固定相和流动相之间做出选择的动力性因素，比如消费倾向研究中的收入增加（消费约束值变大）。我们在此沿用此置换概念，那么载气速度就可以看作为这种动力性因素在组分中分布的一个刻画。如同化学中的组分分子在溶质质量上产生了浓度梯差，经济分析中的组分分子在这种动力性因素（有内因也有外因）的影响下也在分布状态上表现出差异。这种分布差异意味着某些组分分子的运动并不像我们原来预想的那样，从一个塔板进入另一个塔板，而是从聚集的地方扩散到其他塔板上，与此同时，其他组分分子仍然按照原来的进程在两相之间进行分配。如此一来，在浓度梯差形成以后，任何一个时点，有一部分组分分子按照没有扩散作用时的状态进行分配，还有一部分组分分子要么没有进行交换，要么刚刚进入塔板过程，从而引起组分流出时间延长，具体表现为色谱峰的展宽变宽。

以某一个特定的消费区域为例，在这个消费空间中，会存在多种消费形式和消费群体，消费者消费选择会受到多种因素的影响，动力性因素则被假定为消费者可支配收入的增加。如果同样一笔可支配收入增加对不同的消费者具有不同的动力作用，那么消费者消费倾向的表达就会受到影响。例如，考虑消费作为实际收入（=名义收入/通胀率）的函数时的情形。由于消费者对通胀率的了解程度不同，有些人经常关注，在一次收入增加后他们马上能得出增加的实际收入；有些消费者并不关注通胀率，他们会把增加的名义收入作为实际收入（也即“货币幻觉”）。这样，一次收入增加的动力作用是不同的，在我们所假设的A、B两类消费者内部，又各自形成了两类消费者——存在货币幻觉的消费者和不存在货币幻觉的消费者。如果消费函数是建立在实际收入上的，存在货币幻觉的消费者相比没有货币幻觉的消费者更容易选择消费而非储蓄，然而这一抉择并不能反映他们真实的消费倾向。直到他们意识到通胀率的变化时，存在货币幻觉的消费者才能够做出符合其真实消费倾向的消费选择，这样，其在表现出真实消费倾向上就会“滞后”，也就是组分“扩散”，从而使整个组分分离所需要的时间更长，表现在色谱流出曲线上，就是色谱峰变宽，分离效率下降。这些“扩散”产生的原因又都与动力性因素（即可支配收入增加）和组分的性质（即消费者本身内在的某些特质如偏好现金或者具有货币幻觉）有关的。

因此，动力性因素的分布影响了消费者的消费决策，在一定程度上掩盖了他们的真实消费倾向，动力性因素分布差异越大，消费者的真实消费倾向就越难以表达出来，分离不同消费倾向的消费者就更困难，也即流出的色谱峰的展宽变宽。因此，经济学中的分子扩散，可以看作是一种呈非正态分布的随机变量，它虽然在形式上表现为一种“随机游走”状态，但是在时间和空间上又会与一些经济因素存在一定联系，在经济学中，我们通常用解释变量和被解释变量来表示相关经济现象的内在联系。

2.2.2 分子扩散项的影响因素及其置换

根据分子扩散项的公式推导，分别对影响分子扩散项的因素进行分析置换。

（1）弯曲因子γ

色谱柱内固定相的存在，使得组分分子在前进中遇到阻碍而不能自由扩散，因此用γ几何因子校正。化学中γ值的范围通常介于[0,1]之间，当γ=0时，表明阻碍分子运动的阻力越大，分子几乎不能向前移动；当γ=1时，表明分子在运动的过程中几乎无阻碍。

置换到经济学中，当消费者处在一个市场环境中时，总会有各种各样的因素阻碍其继续前进，因此可以将弯曲校正因子γ看作市场对消费者的消费吸引力。γ=0表明市场中某一个商家、产品的吸引力太大，消费者倾向于把个人收入的大部分都用于消费，此时就有可能出现经济过热现象，γ=1表明市场几乎没有消费吸引力。无论γ取0还是取1，都是一种极端状态。结合实际情况，我们假定γ=0.5，即市场对消费者的吸引力处于一种较为均衡的状态。

（2）扩散系数Dg

扩散系数Dg与组分的性质、载气的性质和柱温柱压力有关，这三个影响因素可以置换为：

组分的性质：当组分的分子质量大时，Dg值小。将其进行置换，若待分离的组分为消费者群体，那么可以将分子质量看作某一类消费者在消费者群体中的权重，这部分消费者有比较固定的消费偏好，动力性因素的分布变化并不能够阻碍他们明确表达自己的消费偏好；换句话说在进行消费选择时不容易受到市场环境变化和“从众心理”的影响，这部分的权重越大，在进行消费选择时的扩散系数就越小。

柱温柱压力：当柱温升高时，扩散系数Dg变大；当柱压上升时，扩散系数Dg变小，将其置换到经济现象中，可以将柱温柱压看做是消费者所面临的宏观经济环境的变化，柱温置换为经济的热度，柱压置换为政策环境条件。第一，我们将柱温看做是经济的热度。在经济环境中，我们经常会遇到由于市场需求超过供给所引发的物价指数的全面持续上涨，即经济过热现象，那么在经济过热的环境下，多数消费者都倾向于购买商品，此时单个消费者更易受市场环境和其他消费者群体的影响，就会更倾向于进行消费，消费者之间的相互影响作用就大，扩散系数Dg就会变大。若多数消费者群体都处于观望状态，更倾向于持有货币，那么扩散系数Dg就会下降；第二，将柱压看作是外部政策环境所产生的推动或限制作用，如国家根据市场上货币的供需状况来调整货币和财政政策，提高税收比例、提高存贷款利率以及颁布限购令等。例如，银行提高存贷款利率，就会鼓励消费者将更多的货币进行储蓄，在持有货币有限的情况下，消费者会更倾向于理性消费，此时市场上的各种因素以及“从众心理”的影响就会减小，扩散系数Dg则会下降。那么，在实际的经济运行中，如何将柱温和柱压进行量化呢？我们可以试着用经济环境所产生的数据来进行衡量，柱温用消费价格指数CPI表示，柱压用历年的存款利率表示，这可能会产生一定的局限性，但是在一定时期却能较为准确地反映市场的变化情况。

因此，受消费者权重、作为载气的可支配收入的增加以及宏观经济环境的变化等影响，待分离组分的扩散系数会发生相应改变，它与载气分子质量M的平方根成反比。本文中，将载气分子质量M看作是每次注入的消费者可支配收入的数额，由于化学中扩散系数的范围是0.01～1，为了便于分析，此处假设M=10000，则=0.01。

（3）载气流速u

载气流速也就是载气在柱内单位时间的移动距离，也成为流动相的线速度，是决定色谱分离的重要因素之一，一般而言，当流速高时，色谱峰比较窄，反之色谱峰比较宽，流速u过高或者过低对组分的有效分离都不利。根据化学速率理论方程的耦合式，待分离组分有较好的分离效果时，化学最佳载气流速为。那么，色谱中的最佳载气流速与经济学中厂商利润最大化的条件非常类似，在经济学中，厂商利润最大化的条件是边际收益等于边际成本，也就是MR=MC的交点即为厂商实现利润最大化的均衡点，此时的产量Q便是最佳产量，超过或者低于这个最佳产量Q，厂商利润都不能实现最大化。那么，速率理论中最佳载气流速的经济学置换，也可以考虑将其与一定的经济分析需求相结合。本文将载气线速度u看作是一段时期内消费者可支配收入的平均增长速度，为了便于下文的计算，此处先假设u=0.2。

3 对消费者行为的速率理论置换实例及模拟

本文以塔板理论置换所使用的消费者分类作为分析实例，在已有塔板理论置换研究的基础上，不考虑涡流扩散项和传质阻力项的影响，只对分子扩散项进行置换模拟和实证分析。也就是说，在每一个塔板中，待分离组分不仅在同一塔板的固定相和流动相间进行分配，还会向相邻的塔板进行纵向扩散，这种扩散使得分子流出色谱柱的时间延长，从而造成色谱峰的进一步展宽，使柱效降低，经济主体的行为选择在这种因素影响下发生变化，因此有必要探讨经济中的分子扩散项。

在本文中，对固定相和流动相的置换沿用塔板理论（游士兵,2011）中的置换，将固定相设定为价值，流动相设定为使用价值。同时，在本文以及以后的分析中，都将色谱柱长L看成是消费者所处的比较宏观的消费区域或者消费空间，其取值为L=1。

3.1 有效塔板数的计算及分离过程

在塔板理论（游士兵,2011）的置换模拟中，假设的有效塔板数为n=5，色谱柱长取L=1，则有效塔板高度H=L/n=0.2。

按照上文的假设，扩散系数Dg=0.01，弯曲因子γ=0.5，载气线速度u=0.2，引入分子扩散项，即B/u=2γDg/u=2*0.5*0.01/0.2=0.05，那么新的有效塔板高度变为H’=0.2+0.05=0.25，有效塔板数n=L/H’=1/0.25=4。

以对A类消费者的分配模拟为例：假设A类消费者人数为100人，将该组分加到第0号塔板上，给予他们M元的初始可支配收入，分配比k=1，因此消费者选择消费的倾向为0.5。当可支配收入约束增加，即一次性增加M元的约束v1时，消费者在消费和储蓄之间继续进行选择和分配，使得0号塔板上一半的消费者选择消费并进入1号塔板，1号塔板上同样有一半的消费者由于选择消费进入2号塔板，每继续增加相同的约束时，这个过程就会重复。如表1所示。

表1 分离过程中组分的分布情况

下面分别以单一组分和混合组分的分配为例，对塔板数n=4、考虑分子扩散情况下的组分分配过程进行模拟。

3.2 待分离组分为单一组分的流出曲线

在分子运动的过程中，由于受到浓度梯度的影响，分子总会从高浓度区域向低浓度区域扩散。假定市场中存在这样一群消费者，他们在市场消费中总是处于观望的状态，总是在进行反复考察对比后才会选择消费，在色谱柱中表现为：这部分处于观望状态的消费者从进入色谱柱开始，并不立刻参与第一个塔板上的分配，而是直接流向人数较少的第二个及之后的塔板中进行观望，在色谱柱开始有组分流出，即一部分消费者完成消费过程以后，他们才开始返回到第一个塔板（此时第一个塔板处的组分浓度开始降低）进行消费选择。假定有10%的消费者不直接参与组分的分配，组分在每一塔板上的分配比k=1。由下表，组分在约束增加次数为4时开始流出，那么在之前，在参与分配的组份总数为90，从第五次约束增加开始，10个组分开始参与分配，那么组分人数在塔板上的分配过程可以用表2来表示：

表2 组分人数在n=4,k=1时每个塔板上的分配（考虑分子扩散）

将表2中柱出口的流出人数作为纵坐标，以增加约束次数作为横坐标绘出曲线，得到图1。

图1 n=4时的组分流出曲线

图2 n=5时的组分流出曲线

图1为考虑分子扩散项之后，塔板数n=4时的流出曲线，图2为塔板理论（游士兵，2011）置换中的单一组分A的流出曲线。通过对比可以看到，当考虑组分在相邻塔板间的扩散作用时，待分离组分的流出时间提前，且当组分的流出数为1.8左右时，约束增加次数为18，与塔板数n=5时的约束增加次数16相比，所需要的载气增加，色谱峰相应展宽。

3.3 待分离组分为混合物的流出曲线

以上我们讨论了单一消费者组分在塔板数n=4时的分配过程和峰展宽情况，若待分离组分为混合物，其色谱流出曲线也会有相应变化。借用塔板理论置换（游士兵，2011）中的内容，仍然假定有A类和B类两类消费者，这两类消费者在消费和储蓄上的分配比不同，A类为1:1，B类为1:4，在考虑分子扩散项以后，仍旧假定两类消费者中有相同比例的消费者组分处于观望状态，B类消费者组分在塔板数n=4的塔板上的分配过程与上文类似。

表3 B类消费者在在n=4,k=1/4内每个塔板上的分配（考虑分子扩散）

与塔板数n=5时相比，当塔板数n=4并且考虑组分在相邻塔板间的扩散时，B类消费者的流出曲线分别如图3所示：

图3 n=4时B类消费者流出曲线

图4 n=5时B类消费者流出曲线

由图3和图4对比可知，当考虑组分在相邻塔板间的扩散时，B类消费者的流出曲线仍然有了一定的峰展宽，组分的分离效果相应下降。

同时，在n=4、考虑组分的扩散作用时，将A类消费者按分配比1:1、B类消费者按分配比1:4进行分离模拟，色谱流出曲线图5所示：

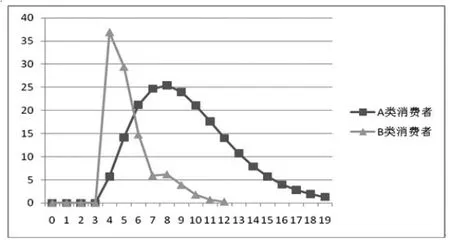
图5 两个混合组分流出曲线图

可以看出，加入分子扩散项以后，待分离组分A和B在经过分离系统后，仍旧形成了两个没有完全分离开的峰，组分分离效果下降。

3.4 结果与分析

由上述两种情况可以看出，当考虑分子扩散项的影响时，色谱分离的塔板高度相应增加，而塔板数相应减少，组分的流出曲线的峰宽明显展宽，由此可以推知，当组分在其他塔板间有更为复杂的扩散作用时，组分从进样到出样的时间将会更加延长，所需要的载气体积增多，流出曲线的峰展宽会进一步增加。

经济社会发展中的经济人行为，受到经济政策环境、居民收入水平、消费者之间的相互影响以及市场对消费者的消费吸引力等多种因素的影响，任何一项因素的变化，都会使组分运动中所受到的阻碍程度（即弯曲因子γ）、扩散系数Dg或者载气线速度u发生改变，引起分子扩散项B/u的改变，从而使得消费者的购买行为发生变化，待分离组分的流出时间提前，组分最终流出时间推迟，组分的分离效果并不是很明显。当消费者所面临的宏观环境不利于消费、个人获得的可支配收入增加幅度减少、以及市场对消费者的消费吸引力下降时，分子扩散项会相应减小，但是与没有考虑分子扩散项时的流出曲线相比，色谱峰依然会展宽。当需要分离的组分为混合组分时，由于各组分的分配系数有差异，不同组分的色谱峰会相应展宽，流出曲线会有较大的重合，从而使得分离效果降低，整个色谱柱的柱效下降。

在实际的经济环境中，分子扩散项是一个不可避免的因素，本研究的一个重要目的，就是对组分在分子扩散项因素影响下的行为表现有一个较为详尽的描述，从而为把握市场环境中的消费者行为、进而制定相应的引导政策提供参考。在理论上，加入分子扩散项对复杂经济现象进行分类模拟，使得色谱经济分析法的运用更加贴近经济现实，在一定程度上弥补了塔板理论的不足，也证明了运用色谱分析法对经济现象进行分类分析具有一定的可行性。

4 总结

作为对塔板理论的补充，速率理论较为充分地考虑了组分分子在色谱柱中运动时的各种扩散过程，为我们控制影响色谱峰展宽的相关因素提供了借鉴。本文在塔板理论的基础上，引入速率理论中的分子扩散项对消费者的行为选择进行了模拟，这与现实生活中消费者的储蓄和消费行为总是受到多种因素的影响比较类似，目的在于描述市场中一些因素的存在使得复杂经济中的组分分离效果不能达到理想状态、分离效率降低的情况，进而为提高分离效果提供建议。

本文只是考虑了速率理论中分子扩散项的影响，涡流扩散项和传质阻力项将在后续文章中进行探讨。同时，对分子扩散项的相应置换，目的在于对经济中所发生的实际状况进行模拟，所设定的数据是为了模拟和演示该理论和方法的可行性，同时由于考虑的局限，整体分析上可能还存在一定的缺陷，在后续关于涡流扩散项、传质阻力项、定性定量分析以及信号检测的研究中有待深入探讨。

[1]游士兵,吴比,沈萍,梅敏,苏正华.复杂经济现象分类方法创新的理论前瞻——基于“化学色谱分析法”的借鉴与思考[J].统计与决策,2011,(7).

[2]游士兵,梅敏,吴比.色谱分析法在经济领域中的应用展望[J].统计与决策,2011,(11).

[3]沈萍,张佩,毛锴苑,李跟强,游士兵.色谱经济分析法置换系列研究：分配比[J].统计与决策，2011,(17).

[4]游士兵,包莉丽,钟双营,管璇,王凌霄.色谱经济分析法置换系列研究：塔板理论[J].统计与决策，2012,(1).

[5]沈萍,乔杨,陈琪瑶,游士兵.色谱经济分析法塔板理论的换例模拟[J].统计与决策，2012,(6).

[6]苏立强.色谱分析法[M].北京：清华大学出版社，2009.

[7]詹益兴.实用色谱法[M].北京：科学技术文献出版社，2008.