基于混合连接函数的最小方差套期保值研究

黄争臻，段元萍

(上海理工大学a.管理学院；b.经济与贸易研究所，上海 200093)

0 问题的提出

套期保值研究的主要内容在于套期保值比率的确定问题。传统的套期保值理论直接采用套期保值比率为1的套保方案，这种方法的缺点是不能对风险与收益等套期保值的目标进行控制，因而适用面很窄。在追求最优化的现代理论基础之上，套期保值理论开始关注对套期保值比率的选择，一个合适的比率有可能得到比传统方法更为有效的结套保果，这也是研究的意义所在。

现有的研究模型主要有两类：一类主要关注降低风险，如最小方差套期保值模型[1]；而另一类在关注风险的同时也考虑组合资产收益，如均值方差套期保值模型[2,3]。

本文主要考虑降低套期保值者的风险，即单独从风险的角度来分析套期保值行为，故选择最小方差套期保值模型来进行研究。现有的基于最小方差的套期保值模型的研究主要问题有两个方面。一方面是对于收益率序列的相互关系上，现有的研究只是利用某单一Copula函数来推导中位数相关系数，忽略了Copula函数对两序列的拟合效果的分析，因此本文结合了阿基米德族的三种Copula模型的优点以及选择偏向上下尾的分位数相关系数来针对收益率波动异常剧烈时期的套期保值问题阐述其合理性。另一方面是对两收益率序列的模型建立上可以改进，用GARCH-t模型来代替以往的GARCH-normal来更好的描述金融时间序列的厚尾特征。

本文以农产品期货品种为例通过实证分析计算套期保值比率，并且与其他传统模型比较套期保值绩效来验证本模型的优越性。

1 最小方差套期保值模型

假设要给Ts单位的某现货资产进行套期保值，构造的套期保值资产组合包括Ts单位多头现货头寸与Tf单位空头期货头寸，t时刻单位现货价格为St，单位期货头寸价格为Ft，忽略保证金与交易费用等因素，至t+1时刻的套保资产组合收益率有：

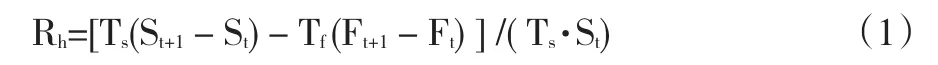
令Rs与Rf分别为现货市场与期货市场的收益率，即

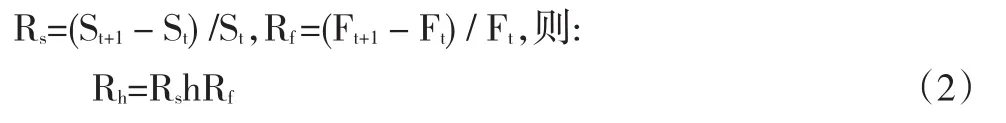
对式（3）取h的二阶导数

其中ρ为现货收益率与期货收益率的相关系数。由式（6）可以看出，利用最小方差套期保值模型计算最优套期保值比率需要进行两方面的估计，一是对期货收益率与现货收益率的标准差进行估计，二是对期货收益率与现货收益率序列的相关系数进行估计。

2 建立模型

2.1 相关系数的确定方法

在相关系数的选择方面，许多研究利用到了Copula中位数相关系数来描述两收益率序列的相关性，但如果近期期货与现货收益率波动剧烈，应用中位数相关系数会缺乏针对性，原因是中位数相关系数即包括了尾部相关的信息，也包括了收益率存在小波动情况下的相关性。如果将分位点往极端移动，度量这种情况下两收益率序列的一致性，并且将其应用到套期保值模型之中来应对近期收益率波动异常剧烈的情况，将得到更好的套期保值绩效。

选择分位点为α与1-α的分位数，得到收益率序列同时高于α或低于1-α分位数的一致性度量指标：

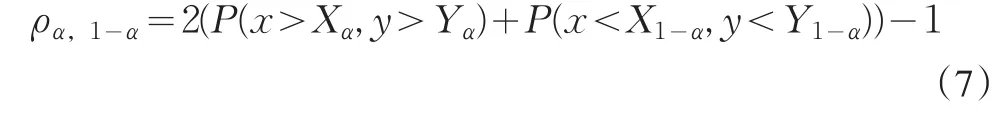
剧烈波动时宜采用偏高的分位点以恰当的反映高波动情况下的相关性，用基于此相关性度量而得到的套期保值比率来集中应对剧烈波动对组合资产收益率的影响。同样的，相关性的分位数测度也可以转化为利用Copula函数求解：

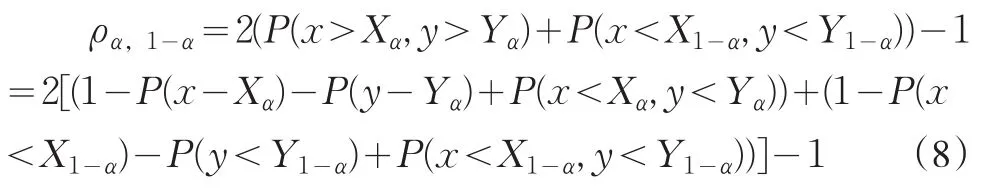
2.2 边缘分布GARCH模型

在计算两收益率序列的标准差方面，实证研究发现，在套期保值之前的历史数据的标准差与套期保值期间的标准差有很大差异[4]，通过引入GARCH模型可以有效的处理标准差的时变性，实现套期保值模型的动态性。而GARCH-t更是对GARCH-normal模型的改进。通过构造一个二元的Copula-GARCH模型，可以完成对边缘分布的拟合，并且通过GARCH模型对收益率序列的波动进行向前预测，另外连接函数可以完成对边缘分布的相关结构的描述，从而通过本模型，完成对最小方差套期保值模型的求解。二元Copula-GARCH-t模型表示为：

其中式（9）与式（10）分别为对现货与期货收益率建立的GARCH(m,n)-t模型，一般假设其中的ε服从正态分布或者标准化的学生t分布以及广义误差分布，通过添加一个动态方程来修正波动从而刻画资产收益率的条件方差的时变特性。另外式（11）表示为用Copula函数对现货与期货收益率建立的联合分布，由于Copula函数对随机变量作单调增变换而不变，因此有：Cε=Cr

于是，我们用概率积分变换的方法来处理边缘收益率序列，所谓概率积分变换是指：用随机变量的密度函数对随机变量进行积分变换，得到一列新的时间序列，其取值范围符合连接函数的输入要求。

2.3 Copula模型的选择

由于金融序列的相关关系的复杂性，一个简单的Copula函数难以将序列间的相关性描述得很透彻，因此，一种更加灵活的Copula函数随之诞生，即混合Copula函数（M-Copula函数），通过构造一个Frank、Gumbel、Clayton三个Copula函数的线性组合：

其中ag+ac+af=1，通过权重的变化可以反映出不同的相关模式，优点在于它包含了以上三种Copula函数各自的特性，在描述相关性时更为有效。

3 套期保值绩效定义与评比方法

本文采用的套期保值绩效采用Ederington(1979)给出的套期保值绩效量化指标[5]，其定义为：参与套期保值与不参与套期保值相比，收益方差的减少程度。指标度量了套期保值之后对风险的降低程度，基于本文从风险这一角度进行套期保值研究，该绩效指标恰好体现了这一出发点。本文的评比方法是通过横向与纵向的比较来观察不同模型的绩效。

（1）横向的对比，比较混合Copula与三种单一Copula模型在套保绩效上的优劣，结果将体现出混合Copula函数在描述期货与现货价格波动关系上的有优异性。第二，比较基于两种不同分位数相关系数的套期保值绩效。

（2）纵向的对比，通过比较市场价格波动平缓与波动剧烈的情况下，传统套期保值模型与Copula模型的套期保值绩效，来体现基于Copula模型计算的相关系数在处理市场价格波动剧烈的情况下的良好性质。

4 中国农产品期货的实证分析

本文采用郑州商品交易所于2011年11月交割的棉花期货价格数据与国内棉花现货价格数据进行套期保值分析。具体来说，棉花期货数据采用棉花期货CF111从2010年11月15日至2011年11月14日共计246个交易日的期货当日结算价；棉花现货价格采用中国棉花信息网统计的与期货价格同时期的每日棉花现货价格数据。其中前180组数据被看做套期保值之前的历史数据来进行模型的估计，后66组数据所在期间视为套期保值期间。

4.1 计算收益率波动值

首先根据期货与现货收益率的自相关与偏自相关情况，对期货和现货收益率模型误差项进行ARCH效应检验的结果，发现AR模型残差平方具有异方差性，可以在此基础上建立GARCH模型。

选取棉花期货合约的交易日期货合约价格Pf与同种产品的每日现货价格Ps，对数收益率乘以100放大数据可以提高后续计算的精度，构造对数收益率如下：

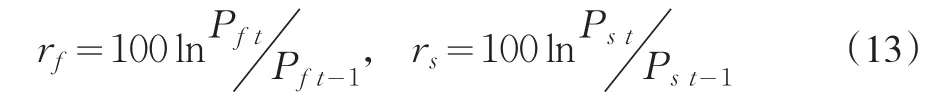
首先按照式（13）将所有价格数据进行处理之后得到收益率序列，再对期货收益率序列建立GARCH-t模型参数估计结果如下：

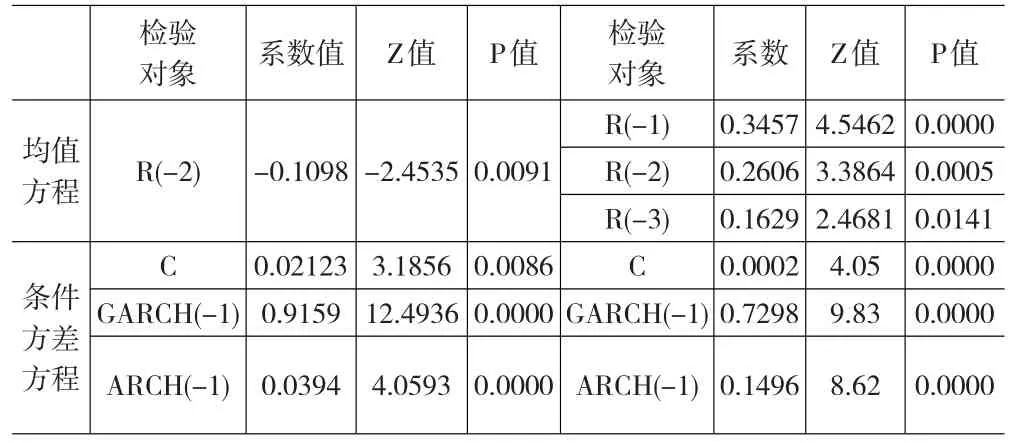
表1 GARCH模型参数检验表

如表1所示各参数估计值的概率值在0.05的显著性水平下均通过检验，因此估计出的两个模型各系数均具有显著性。随后的ARCH效应检验F与LM统计量对应概率均大于0.8，即消除了AR模型误差项的异方差性。于是，可以直接利用估计出的GARCH模型的GARCH方程得到：σf=0.05356，σs=0.06866

由于Copula模型对输入样本的要求，利用已经建立好的期货与现货收益率序列的GARCH模型，依靠MATLAB对收益率序列进行概率积分变换，对变换后的序列进行K-S检验结果见表2。由结果可知，检验结果不能拒绝原假设，能够继续建立Copula模型。

表2 序列的均匀分布检验结果

4.2 计算相关系数

4.2.1 Copula模型的参数估计及拟合优度评价

估计混合Copula模型的参数，如式（12）所示，由于混合Copula参数较多，其极大似然函数比较复杂，不能用一般的方法进行参数估计，因此借助Matlab采用EM算法来进行估计。结果及拟合优度检验结果见表3。

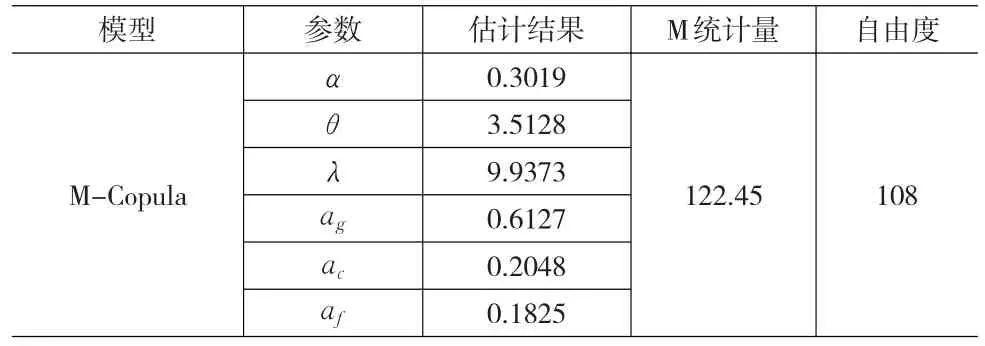
表3 Copula模型参数估计结果

表3中各参数估计值在0.05水平下均显著。由进行拟合优度检验得到的M统计量值122.45小于对应自由度的卡方分布分位数，因此通过检验，认为该Copula模型对实际分布的拟合效果理想。

4.2.2 基于Copula模型的相关系数与套期保值比率的计算

由于观察到所采用的收益率数据波动比较明显，因此在偏向尾部的相关系数的选择上尝试采用α=0.7，按照式（7）与式（8）所示，计算中位数相关系数与α分位数相关系数，将已估计出的参数以及对收益率序列进行概率积分变换之后的序列代入式中，相关系数ρ0.5,0.5=0.6980，ρ0.7,0.3=0.6773

根据最小方差套期保值比率的计算公式（6），将期货、现货收益率标准差以及相关系数代入，分别得到基于α分位数相关系数的最优套期保值比h1=0.8682与基于中位数相关系数的最优套期保值比h2=0.8948。

4.3 套期保值绩效分析

4.3.1 基于M-Copula-GARCH的套期保值绩效

以基于α=0.7的分位数相关系数计算的最优套期保值比率h1进行套期保值交易，对2011年8月13日之后的数据对套期保值进行绩效分析，绩效度量指标为式Ederington给出的套期保值绩效量化指标HP，反应组合资产相对于不进行套期保值而言，使收益方差的减少程度。计算结果为HP1=0.6524228。另外计算基于中位数相关系数的套期保值绩效记为HP2=0.6109731。

4.3.2 基于其他套期保值模型的套期保值绩效

（1）完全套期保值模型：本模型完全不考虑历史数据，直接用1作为套期保值比率，其套期保值绩效记为HP3=0.4347362。

（2）线性回归套期保值模型：本模型直接对套期保值之前的历史数据采用最小二乘法作回归，采用回归系数作为最优套期保值比率，回归系数为1.1826，计算得到套期保值绩效结果为HP4=0.3725177。

（3）传统最小方差套期保值模型：本模型的最优套期保值比率计算式与本文采用的计算式相同，同为式（6），不同之处是其中的相关系数采用的是历史数据的线性相关系数，两个收益率的标准差直接采用历史数据的标准差，其计算结果HP5=0.3195228。

4.3.3 绩效评比与结果

表4 套期保值绩效比较

通过纵向比较发现，基于M-Copula-GARCH的最优套期保值模型得到了最优的绩效，买入了较少的期货头寸，却更好的屏蔽了风险，这种功效源于模型对数据关系的更贴切的分析与描述。而线性回归套期保值与传统的最小方差模型的套期保值绩效甚至不如最简单的完全套期保值，这是由于特定收益率序列的选择导致序列之间的非线性相关关系占据了主要地位导致线性模型失效。横向对比基于两种不同的分位数相关系数的方法，当数据的波动比较大的时候，基于偏向尾部的相关系数得到了稍好的套期保值绩效。同时混合Copula模型提高了分布的拟合效果。

因此，通过本研究的模型进行套期保值提高了套期保值绩效，能有效的规避现货市场的风险。

5 小结

第一，本文对农产品期货与现货收益率建立起了M-Copula-GARCH模型，通过实证分析验证了其描述序列及序列之间相关性的理想效果。第二，利用Copula模型对期货与现货收益率拟合联合分布，在模型的选择上进行了择优，从而使得到的相关系数比起传统的线性相关系数有了很大的改进。第三，收益率的方差采用GARCH-t模型估计，改进之处主要体现在其动态性上；而相关系数则利用到了Copula模型在描述非线性相关上的优势，采用了相对中位数相关系数更优的α分位数相关系数。第四，对比不同的模型，综合横向与纵向的评比结果来体现本研究方法更好的套保效果。

[1]Ederington,L.H.The Hedging Performance of the New Futures Mar⁃kets[J].Journal of Finane,1979,(34).

[2]David H.Risk,Futures Pricing,and the Organization of Production in Commodity Markets[J].Journal of Political Economy,1988,(96).

[3]Holmes P.Exante Hedge Ratios and the Hedging Effectiveness of the FTSE-100 Stock Index Futures Contracts[J].Applied Economic Let⁃ters,1995,(2).

[4]仇晓光，周颖.基于协整理论的期货套期保值决策模型研究[D].大连理工大学,2008.

[5]Ederington,L.H.The Hedging Performance of the New Futures Mar⁃kets[J].Journal of Finane,1979,(34).