基于有限域上仿射空间构造新码本

刘雪梅，贾丽华

（中国民航大学理学院，天津300300）

一个参数为（N，K）的码本C 是由N个单位向量{c1，c2，…，cN}构成的集合，ci长度为K，其中，1≤i≤N。码本作为信息的载体可用于传输不同的信息，且有着低重复率、强保密性的优点。在实际应用中，对于一定的长度K，希望码本的向量个数N尽可能大，而最大相关幅度尽可能小，这样可以降低信号之间的相互干扰。然而，码本的参数受到理论界限的制约，其最大相关幅度和参数N和K之间满足一定的界，即Welch 界[1]。当N≥K时，如果码本C 的最大相关幅度能达到Welch界，则称码本C 为MWBE（maximal Welch bound equality codebook）码本或最优码本[2]。MWBE 码本仅存在于非常有限的码字个数和码字长度的条件下。对MWBE 码本的研究，主要有以下几方面：①任意N＞1，由m序列构造参数为（N，N-1）的MWBE 码本；②任意N＞1，基于离散傅里叶变换构造（N，N- 1）的MWBE 码本，基于ZN中的（N，K，λ）差集构造参数为（N，K）的MWBE 码本[3]；③设d是一个给定的正整数，当N=2K=2d+1或N=2K=pd+1，且p是素数时，用协商矩阵构造参数为（N，K）的MWBE 码本[4-5]；④采用有限域Fq中的（N，K，λ）循环差集[2]和阿贝尔差集[6]构造参数为（N，K）的MWBE 码本；⑤用（2，k，υ）施泰纳坦纳系构造参数为（N，K）的MWBE 码本[7]；⑥采用图论和有限几何构造参数为（N，K）的MWBE 码本[8-10]。

最优码本的约束条件较严格、限制因素较多，因此，构造最优码本的方法较少且难以构造达到Welch界的最优码本。码本的最大相关幅度渐近达到Welch界时，称为渐近最优码本，即放宽了码本的约束条件，使得参数选取更加灵活。同时，当码本中的码字足够长时，渐近最优码本与最优码本性质相似，因此，构造渐近最优码本是一个折中的方法。Ding 等[11]提出了利用几乎差集构造近似最优码本的方法，但满足条件的几乎差集较少；Yu[12]从二元序列出发构造了几乎最优码本，但对初始矩阵的条件限制严格；Heng[13]利用广义雅可比和构造了几类渐近最优码本；Zhang 等[14]基于分圆类的几乎差集构造了限制条件更宽松的渐近最优码本，又利用高斯和构造了近似达到Welch 界的渐近最优码本，解决了文献[11]中遗留的问题。

目前，构造渐近最优码本的方法较少，且难以找到满足条件的参数。针对以上问题，提出了一个构造码本的新方法，且新码本渐近达到Welch 界的条件较为宽松。

1 基础知识

1.1 码本的相关概念及界

定义1一个参数为（N，K）的码本C是由N 个1×K 个单位向量构成的集合{c1，c2，…，cN}，其中，向量ci称为码本的码字，0≤i≤N。

定义2码本C的最大相关幅度定义为

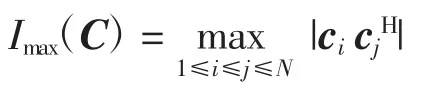
式中cjH表示复数向量cj的共轭转置。

引理1（Welch 界）对任意参数为（N，K）的码本C，且N≥K，有

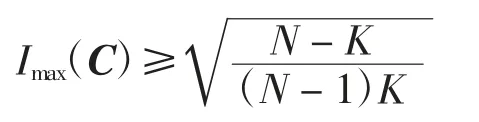
1.2 仿射空间的相关概念及计数定理

设Fq是一个q 元有限域，其中q 为素数的幂。对于一个非负整数n，表示Fq上的n 维行向量空间。qn )中的任意非零向量和零向量都称为点，任意1 维向量子空间的陪集称为线，任意2 维向量子空间的陪集称为面。中的任意r（0≤r≤n）维向量子空间的陪集称为仿射r-flat，或简称为r-flat。

设U+u是一个r-flat，V+v是一个s-flat，其中，U是一个r 维向量子空间，V是一个s 维向量子空间，u，v∈。如果u∈V+v且U⊂V，则称r-flat⊂s-flat。若r-flat⊂s-flat 或s-flat⊂r-flat，则称其是相关联的。点集与r-flat（0≤r≤n）及其之间的关联关系称为Fq上的n 维仿射空间，记作AG（n，Fq）。

参考文献[15]中有以下定理及定义。

定理1设0≤m≤n，则AG（n，Fq）中的m-flat的个数为。

定理2设0≤k≤m≤n，则AG（n，Fq）中包含于某一给定的m-flat中的k-flat的数量为。

定理3设0≤k≤m≤n，则AG（n，Fq）中包含一个给定的k-flat的m-flat的数量为。

定义3设a=（a1，a2，…，an）是中的向量，则向量a的Hamming 权定义为非零分量ai的个数，表示为ω（a），即

ω（a）=|{i|1≤i≤n，ai≠0}|

2 构造新的码本

在构造新的码本之前，先利用有限域上仿射空间的关联关系构造一类二元码。

定义4给定整数0≤k≤m≤n，令M（k，m，n）是一个二元矩阵，其中，行是由所有的k-flat标定，列是由所有的m-flat标定，M（k，m，n）的第i 行第j 列为1当且仅当第i 行的k-flat包含在第j 列的m-flat中。

由定理1 可知M（k，m，n）是一个K×N 的矩阵，且其列权重都是ω，其中，，。

由此，以每列为一个码字，就得到了一个二元等重码C，参数为（K，N）。对任意一个二元码C，可定义码本为

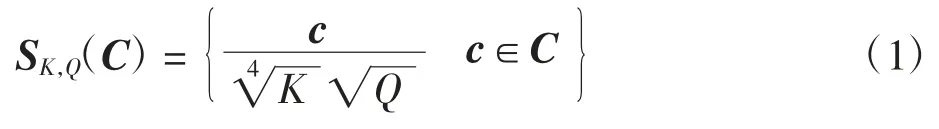
引理2对任一（K，N）二元码C，在式（1）中定义的集合SK，Q（C）是一个（K，N）码本，且最大相关幅度为。

证明所构造码本的大小和码字的长度可由二元码C 的定义及参数得出。

对任意两个不同的向量si，sj∈SK，Q（C），有

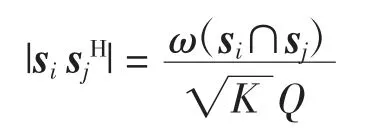
设第i 个m-flat 为U+u，第j 个m-flat 为V+v，其中，U，V 表示m 维向量空间，u，v∈。ω（si∩sj）取得最大值，当且仅当（U+u）∩（V+v）=W+w，其中，W 是一个m-1 维向量空间，w∈，则W+w 是一个（m-1）-flat。那么ω（si∩sj）的最大值为

定理4若SK，Q（C）是一个最优码本，当且仅当k=n。

证明若SK，Q（C）是一个最优码本，当且仅当，即K=1，则k=n。

定理5当（n-m-1）m ＞（n-k-1）k 时，SK，Q（C）是一个渐近最优码本。

证明（N，K）码本SK，Q（C）的参数为

由于（n-m-1）m ＞（n-k-1）k，则

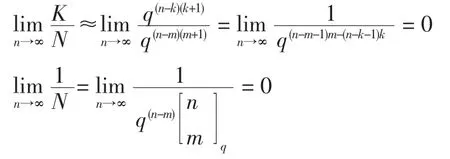
则可得到

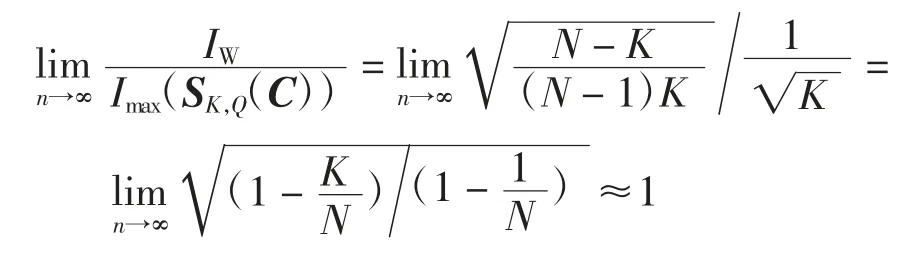
因此，SK，Q（C）是一个渐近最优码本。

3 结语

基于有限域上仿射空间提供了一个构造码本的一般方法。首先利用仿射空间之间的包含关系构造一类二元等重码，然后用二元等重码构造了最大相关幅度为的码本。码本SK，（QC）是最优码本的充要条件是k=n。当（n-m-1）m ＞（n-k-1）k 时，码本SK，Q（C）渐近达到Welch 界，是一个渐近最优码本。