非连通图C3（m，0，0）∪G的优美性

2013-12-21 13:26吴跃生

华东交通大学学报 2013年6期

吴跃生

（华东交通大学基础科学学院，江西南昌330013）

1 引言与概念

本文所讨论的图均为无向简单图，V(G)和E(G)分别表示图G的顶点集和边集，记号[m,n] 表示整数集合{m,m+1,…,n} ，其中m和n均为非负整数，且满足0 ≤m＜n。未说明的符号及术语均同文［1］。图的优美标号问题是组合数学中一个热门课题［1-10］。

定义2［1］设f为G的一个优美标号，如果存在一个正整数k，使得对任意的uv∈E(G)有

f(u)＞k≥f(v)或f(u)≤k＜f(v)

成立，则称f为G的平衡标号（或称G有平衡标号f），且称k为f的特征。图G称为平衡二分图（balanced bipartite graph）。

显然，若f为G的平衡标号，则k是边导出标号为1的边的两个端点中标号较小的顶点的标号。

定义3［1］在平衡二分图G中，设其优美标号θ的特征为k，并且θ（u0)=k，θ（v0)=k+1，则称u0为G的二分点，v0为G的对偶二分点。

定义4［2］G是一个优美二部图，其优美标号为θ，V(G)划分成两个集合X，Y，如果，则称θ是G的交错标号。称G是在交错标号θ下的交错图。

定义5［3-4］V(G)={v1,v2,…,vn}的每个顶点vi都粘接了ri条悬挂边（ri为自然数，i=1,2,…，k）所得到的图，称为图G的(r1,r2,…,rn) -冠，简记为G(r1,r2,…,rn)。特别地，当r1=r2=…=rn=r时，称为图G的r-冠。图G的0-冠就是图G。

本文讨论了非连通图C3(m,0,0)⋃G的优美性。

2 主要结果及其证明

定理1设G是一个p条边的优美图，g是G的优美标号，p-1 不是g的标号值，h是图H特征为k的交错标号，k+2 不是h的标号值（k+2 ＜q，|E(H)| =q）则非连通图G⋃H存在k+1 不是其标号值的优美标号。特别地，当G是交错图时，则非连通图G⋃H存在k+1不是其标号值的交错标号。

证设X，Y是交错图H的一个二分化，且=k+1，|E(H) |=q。

定义非连通图G⋃H的顶点标号θ为

下面证明θ是非连通图G⋃H的优美标号。

1）θ：X→［0，k］是单射（或双射）；θ：Y→［k+1+p，p+q］-｛k+2+p｝是单射（或双射）；θ：V(G)→［k+2，k+2+p］-｛k+1+p｝是单射（或双射）；容易验证：θ：V(G⋃H)→［0，p+q］-｛k+1｝是单射（或双射）。

2）θ′：E(G)→［1，p］是双射。θ′：E(H)→［p+1，p+q］是双射容易验证：θ′：E(G⋃H)→［1，p+q］是一一对应。

由1）和2）可知θ就是非连通图G⋃H的缺k+1标号值的优美标号。

特别地，当G是交错图时，设X1，Y1是图G的一个二分化，且=k1+1 ，令X2=X⋃X1，Y2=Y⋃Y1，有=k1+k+2 ＜=k1+k+3 则非连通图G⋃H存在k+1不是其标号值的特征为k1+k+2 的交错标号。证毕。

引理1对任意自然数m，C3(m,0,0)存在缺标号值m+2 的优美标号。

证设圈C3的顶点依次为v1,v2,v3，与顶点v1邻接的端点（或叶）记为x1,j(j=1,2,…,m)，定义非连通图C3(m,0,0) 的顶点标号θ为：θ(v1)=3+m，θ(v2)=m，θ(v3)=m+1，θ(x1,j)=m-j,j=1,2,…,m，（当m=0 时，θ(x1,j)=θ(v1)）。

容易验证：θ就是C3(m,0,0)缺标号值m+2 的优美标号。

定理2对任意自然数m，图G是特征为k且缺k+2 标号值的交错图（k+2 ＜q，|E(G)| =q），则非连通图存在缺标号值k+1的两种不同的优美标号。

证由定理1 和引理1，可给出非连通图C3(m,0,0)⋃G的第一种优美标号，下面给出非连通图C3(m,0,0)⋃G的第二种优美标号。

设圈C3的顶点依次为v1,v2,v3，与顶点v1邻接的端点（或叶）记为x1,j(j=1,2,…,m)，设X,Y是图G的一个二分化，θ1是图G的交错标号，且=k+1。

定义非连通图C3(m,0,0)⋃G的顶点标号θ为

θ(v1)=k+2,θ(v2)=3+k,θ(v3)=5+k+m,θ(x1,j)=3+k+j，j=1,2,…,m，（当m=0 时，θ(x1,j)=θ(v1)），

下面证明θ是非连通图C3(m,0,0)⋃G的优美标号。

1）θ：X→［0，k］是单射（或双射）；θ：Y→［k+m+4，q+m+3］-｛k+m+5｝是单射（或双射）；θ：V(C3(m,0,0)) →［k+2 ，k+m+3］⋃k+m+5 是双射；容易验证：θ：V（C3(m,0,0)⋃G）→［0，q+m+3］-｛k+1｝是单射（或双射）。

2）=1+j,j=1,2,…,m;=1,=2+m,=3+m,：E(C3(m,0,0))→［1，m+3］是双射；：E(G)→［m+4，q+m+3］是双射。

由1）和2）可知θ就是非连通图C3(m,0,0)⋃G的缺k+1标号值的优美标号。证毕。

例1由定理2可得非连通图C3(4,0,0)⋃C4缺标号值2的第一种优美标号为：C3（4，0，0）：10（3，4，5，6），7，8；C4：0，11，1，9；由定理2可得非连通图C3(4,0,0)⋃C4缺标号值2的第二种优美标号为：C3（4，0，0）：3（5，6，7，8），4，10；C4：0，11，1，9。

引理2［1］对任意自然数m，n，当m≥2，n≥2 时，完备二分图Km,n存在特征为m-1 且缺m+1 标号值的交错标号。

证设完备二分图Km,n的顶点二分划为V1，V2，V1={v1,v2,…,vm}，V2={u1,u2,…,un}，令

θ(vi)=i-1,θ(vi)=i-1,i=1,2,…,m，θ(ui)=im,i=1,2,…,n

容易验证：对任意自然数m，n，当m≥2，n≥2 时，完备二分图Km,n存在特征为m-1 且缺m+1 标号值的交错标号。

由引理2和定理2，有

推论3对任意自然数h，m，n，当m≥2，n≥2 时，非连通图C3(m,0,0)⋃Km,n存在且缺标号值m的两种不同的优美标号。

例2由推论3可得C3(4,0,0)⋃K3,2缺标号值3的两种不同的优美标号如图1所示。

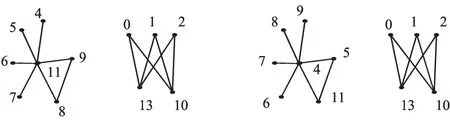
图1 非连通图C3(4,0,0)⋃K3,2 的两种优美标号Fig.1 The graceful labeling of C3(4,0,0)⋃K3,2

我们把顺序有一个公共点的m个C4的连通并图记作Fm,4［1］。

引理3［1］对任意自然数m，图Fm,4存在特征为m且缺m+2 标号值的交错标号。

由引理3和定理2，有

推论4对任意自然数m，n，非连通图C3(m,0,0)⋃Fn,4存在缺标号值n+1的两种不同的优美标号。

例3由推论4可得C3(4,0,0)⋃F3,4缺标号值4的两种不同的优美标号如图2所示。

图2 非连通图C3(4,0,0)⋃F3,4 的两种优美标号Fig.2 The graceful labeling of C3(4,0,0)⋃F3,4

我们把m个C4间顺序加一条边的图记作∧C4,m［1］。

引理4［1］对任意自然数m，图∧C4,m存在特征为2m-1且缺2m+1标号值的交错标号。

由引理4和定理2，有

推论4对任意自然数m，n，非连通图C3(m,0,0)⋃∧C4,n存在缺标号值2n的两种不同的优美标号。

例4由推论4可得C3(4,0,0)⋃∧C4,2缺标号值4的两种不同的优美标号如图3所示。

图3 非连通图C3(4,0,0)ΛC4,2 的两种优美标号Fig.3 The graceful labeling of C3(4,0,0)ΛC4,2

引理5［1］对任意自然数a,b，图C4(a,0,b,0)存在特征为1且缺3 标号值的交错标号。

证设C4上的顶点依次为u1,u2,u3,u4，与顶点u1邻接的端点（或叶）记为y1,j，j=1,2,…,a，与顶点u3邻接的端点（或叶）记为y3,j，j=1,2,…,b。

定义C4(a,0,b,0) 的顶点标号θ为：θ(u1)=0,θ(u3)=1，θ(u4)=2 ，θ(y1,j)=5+a+b-j,j=1,2,…,a,（当a=0 时，θ(y1,j)=θ(u1)），θ(u2)=4+b,θ(y3,j)=4+b-j，j=1,2,…,b,（当b=0 时，θ(y3,j)=θ(u3)）。

下面证明θ是C4(a,0,b,0)的优美标号。

1）容易验证：θ：V(C4(a,0,b,0))→[0,4+a+b]-{3}是一一映射。

2）(u1u2)=|θ(u1)-θ(u2)|=4+b,(u3u2)=|θ(u3)-θ(u2)|=3+b,(u3u4)=|θ(u3)-θ(u4)|=1,=|θ(u1) -θ(u4)|=2,(u1y1,j)=|θ(u1) -θ(y1,j)|=4+a+b-j,j=1,2,…,a，(u3y3,1)=|θ(u3)-θ(y3,1) |=3+b-j,

由1）和2）可知θ是C4(a,0,b,0)的优美标号。

令X={u1,u3}，Y={u2,u4}⋃{y1,j|j=1,2,…,a}⋃{y3,j|j=1,2,…,b}则有

所以，θ就是图C4(a,0,b,0)特征为1，且缺3的交错标号。

由引理5和定理2，有

推论5对任意自然数a,b,m，非连通图C3(m,0,0)⋃C4(a,0,b,0)存在缺标号值2 的两种不同的优美标号。

例5由推论5可得C3(4,0,0)⋃C4(3,0,5,0)缺标号值2的两种不同的优美标号如图4所示。

图4 非连通图C3(4,0,0)⋃C4(3,0,5,0)的两种优美标号Fig.4 The graceful labeling of C3(4,0,0)⋃C4(3,0,5,0)

［1］马杰克.优美图［M］.北京：北京大学出版社，1991：1-247.

［2］杨显文.关于C4m蛇的优美性［J］.工程数学学报，1995，12（4）：108-112.

［3］吴跃生.关于圈C4h的（r1，r2，…，r4h）-冠的优美性［J］.华东交通大学学报，2011，28（1）：77-80.

［4］吴跃生，李咏秋.关于圈C4h+3的（r1，r2，…，r4h）-冠的优美性［J］.吉首大学学报：自然科学版，2011，32（6）：1-4.

［5］吴跃生.关于图P6k+53∪Pn3的优美性［J］吉首大学学报：自然科学版，2012，33（3）：4-7.

［6］吴跃生，徐保根.两类非连通图(P2∨)(0，0,r1,0,…,0,rn)⋃St(m)及(P2∨)(r1+a,r2,0,…,0)⋃Gr的优美性［J］.中山大学学报：自然科学版，2012，51（5）：63-66.

［7］吴跃生.图C7（r1，r2，r3，，r4，r5，0，0）∪St（m）的优美性［J］.吉首大学学报：自然科学版，2012，33（5）：9-1.

［8］吴跃生，王广富.关于C4h+1⊙K1的（Gr1，Gr2，…，Gr4h+1，Gr4h+2）-冠的优美性［J］.山东大学学报，2013，48（4）：25-27.

［9］吴跃生.关于圈C4h+3的（Gr1，Gr2，…，Gr4h+3）-冠的优美性［J］.吉首大学学报：自然科学版，2013，34（4）：1-6.

［10］吴跃生，王广富，徐保根.非连通图C2n+1∪Gn-1的优美性［J］.华东交通大学学报，2012，29（6）：26-29.