关于顶点染色的一个猜想

张祥波

(德州市临邑县临盘中学，山东 德州 251507)

1 引言

有关的术语和记号参见文献[1]。用G表示一个简单有限无向图，设χ(G)、|S|、Δ(G)分别表示图G的顶点染色数、最大团的顶点数、最大度，|V(G)|表示图G的顶点数，记作p=|V(G)|。图G中含有的所有最大团K|S|的公共顶点及其在图G中的边构成的子图，记作图GS(V′,E′),简称图GS。V′，E′分别是图GS的顶点集和边集。用G-V′表示从G中删去V′(GS)的所有顶点及其与V′(GS)中顶点关联的一切边后得到的图。

图的顶点染色是一个长期且困难的问题，对图的结构进行正确合理地划分，是研究顶点染色的关键。文献[2-4]基于图的结构给出了一些特殊图的顶点染色，文献[5-7]从算法方面探讨图的顶点染色。从划分图的结构出发，文献[8]研究了一些特殊图的顶点染色数，文献[9-11]证明了以下结论。

定理若|S|∈{p,p-1,p-2,p-3,p-4,p-5}，则χ(G)≤|S|+1。

本文继续探讨这个结论，提出一个新的猜想：χ(G)≤|S|+C，C∈Z+且C为常数。若C=1，我们证明对于|S|=p-6的一些图，有χ(G)≤p-5。

定义1[8]如果图G含有的所有最大团存在公共顶点，且公共顶点的个数为k，则称此图为第k类图。

引理1[11]若|S|=p-5,则χ(G)≤p-4。

引理2[2]图G是二部图，当且仅当G中不含奇圈。

引理3[9]若|S|=p-2,则χ(G)=p-2。

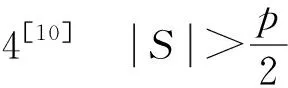
2 |S|=p-6的一些图

证明设顶点u∈V′(GS),顶点v∈V(G-V′),u和v不相邻。将顶点u和v删掉，必得到一个顶点数是p-2且|S|=p-7的图G′,由引理1知，χ(G′)≤p-6。添上顶点u和v，就得到原来的图G，而色数最多增加1，故χ(G)≤p-5。

由定理1的证明知推论成立。

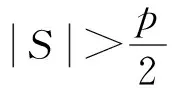
(1)V′(GS)中任意一个顶点与V(G-V′)中的所有顶点相邻；

(2)图G是第p-7类图,

则χ(G)=p-6。

证明由于图G是第p-7类图，V′(GS)中任意一个顶点与V(G-V′)中的所有顶点相邻，且|S|=p-6；则图G-V′是顶点数为7的无边图。故χ(G-V′)=1。而图GS有p-7个顶点，且是一个团；故染p-7种颜色。因为V′(GS)中任意一个顶点与V(G-V′)中的所有顶点相邻，所以χ(G)=p-6。

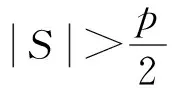
(1)V′(GS)中任意一个顶点与V(G-V′)中的所有顶点相邻,

(2)图G是第p-8类图,

则χ(G)≤p-5。

证明由图G满足的2个条件知，图GS是顶点数为p-8的团,G-V′是顶点数为8且含最大团K2的图。于是0≤Δ(G-V′)≤7。0≤Δ(G-V′)≤2时，G-V′可分解成一些孤立点或路或圈等连通分支的并，易得χ(G-V′)≤3；Δ(G-V′)=k≥3时，设v0为k度点且v0与{v1,v2,…,vk}相邻，则G-V′-{v0,v1,v2,…vk}中至多有8-(k+1)≤4个点，又不含K3，从而为二部图，所以v0用颜色1染，{v1,v2,…,vk}中的点用颜色2染，其余点用颜色1和3染即可。从而χ(G-V′)≤3，结合(1)和(2)，故χ(G)≤p-5。

推论2p=8且含最大团K2的图G,则χ(G)≤3。

由定理3的证明知推论2成立。

3 待解决的问题

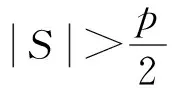
(1)V′(GS)中任意一个顶点与V(G-V′)中的所有顶点相邻,

(2)图G是第p-k类图(k=9,10,11,12),

则是否有χ(G)≤|S|+1？