基于前馈补偿的关节机器人轨迹跟踪控制研究
姜峰
(泰州职业技术学院,江苏 泰州 225300)
机器人技术被认为是对未来新兴产业发展具有重要意义的高新技术之一,多关节机器人技术的研究已从传统的工业领域扩展到医疗服务、教育娱乐、勘探勘测、生物工程和救灾救援等领域[1-3]。由于关节机器人结构紧凑、占空间小、灵活、工作空间较大、避障性能好,目前广泛应用于工业机器人和轮式或履带式排爆机器人中。目前,针对机器人轨迹跟踪控制的研究方法从类别上看大致分为经典控制方法、现代控制方法、智能控制方法等。经典控制方法通常利用传统的控制策略,主要研究对象是单输入单输出系统,最具代表的是PID控制[4]。现代控制方法区别于传统的控制方法,将适用范围从单输入单输出系统拓展到了多输入多输出系统,目前具有代表性的现代控制方法有鲁棒控制、滑模变结构控制、自适应控制等[5-6]。常见的智能控制方法有神经网络算法、模糊控制算法、遗传算法、粒子群算法、迭代学习算法等[7-9]。
在目前的研究成果中,跟踪控制问题存在达到稳态的响应时间长、系统鲁棒性较差、很难获得较好的系统动静态品质等问题。针对以上不足,本文利用常规PID控制设计前馈补偿项,有效提高了系统的跟踪性能和快速响应能力,同时能有效抑制干扰,提高系统的鲁棒性,保证系统获得较好的动静态品质。
1 关节机器人动力学模型
假设某机械臂具有n个自由度[10],其广义坐标即关节变量,用n维矢量θ表示,则机械臂系统的欧拉-拉格朗日方程为:
(1)
其中,T代表动能;τ是n维矢量。经推导可得出带有不确定性因素的机器人动力学方程[11]为:
(2)
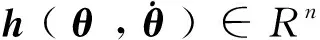
对 (2)式,设计控制器的目标是利用合适的控制方法最终实现关节机器人系统的鲁棒跟踪控制,即实现lim(θd-θ)=0(t趋于无穷时),其中,目标输出角度即θd,实际输出角度为θ。
2 控制器设计
控制器由两部分组成[11]。
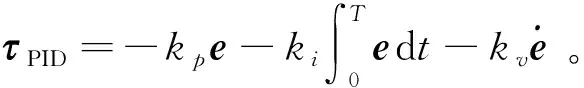
(2)前馈控制器。基于前馈补偿的思想[12-13],采取完全补偿策略则有表达式:
则总的控制力矩:
(3)
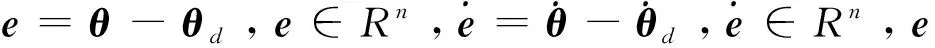
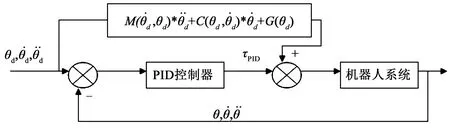
图1 基于前馈补偿的控制框图Fig.1 Control block diagram based on feed-forward compensation
3 仿真分析
对于GR-II两关节机器人系统,考虑系统不确定性时系统动力学方程可描述为[11]:
(4)
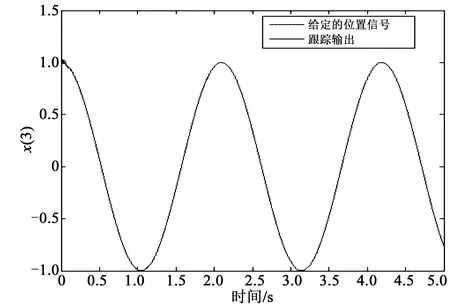
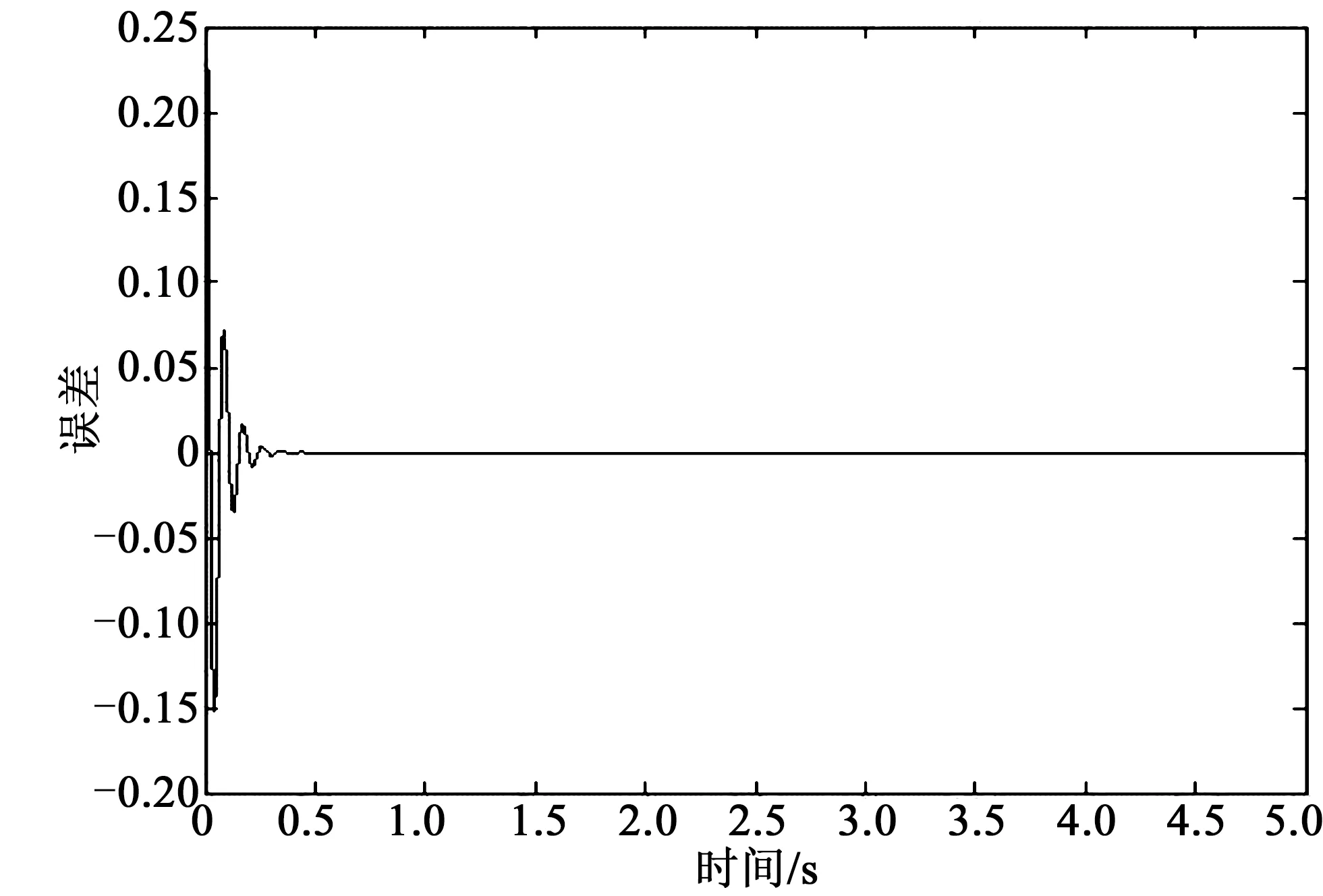
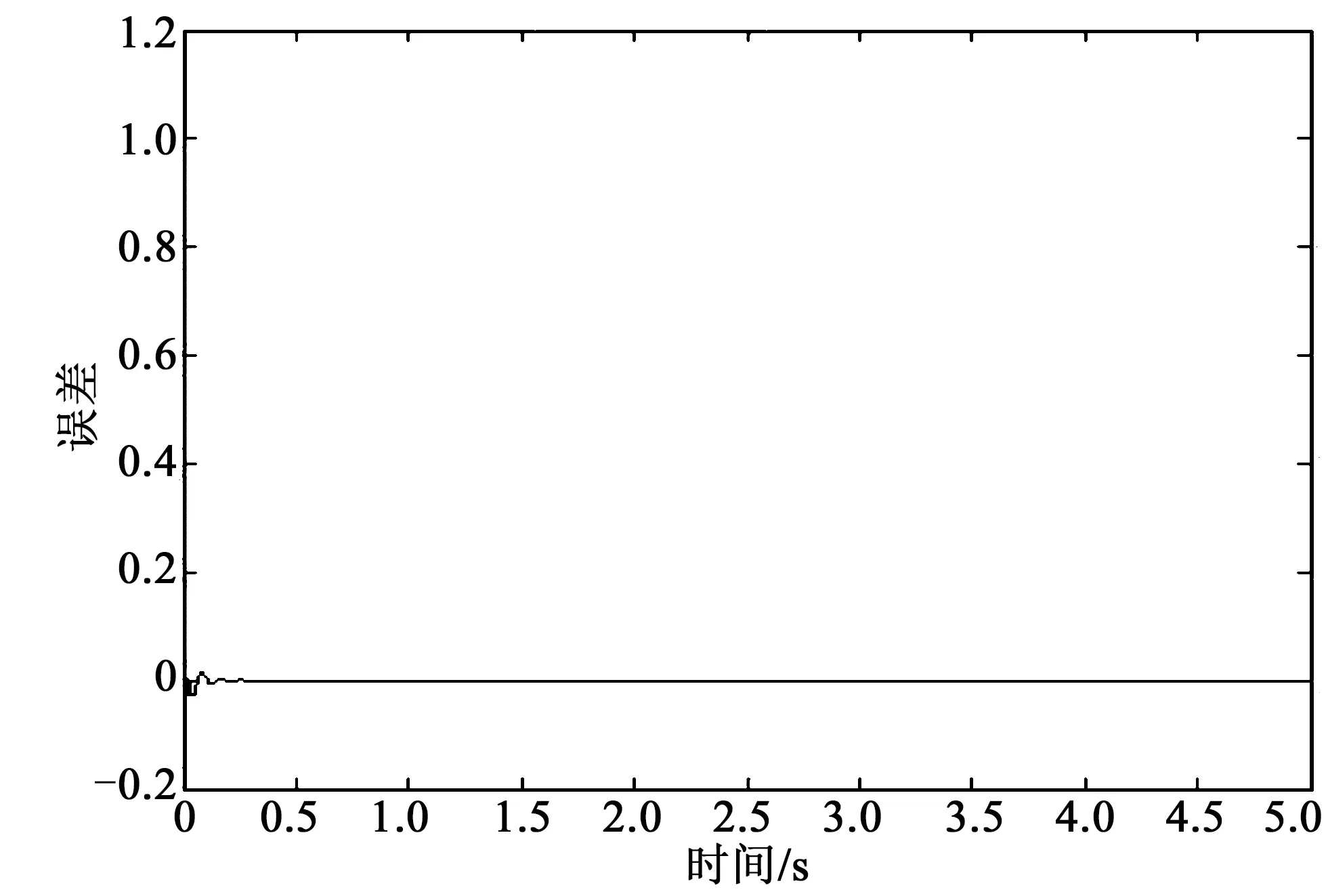
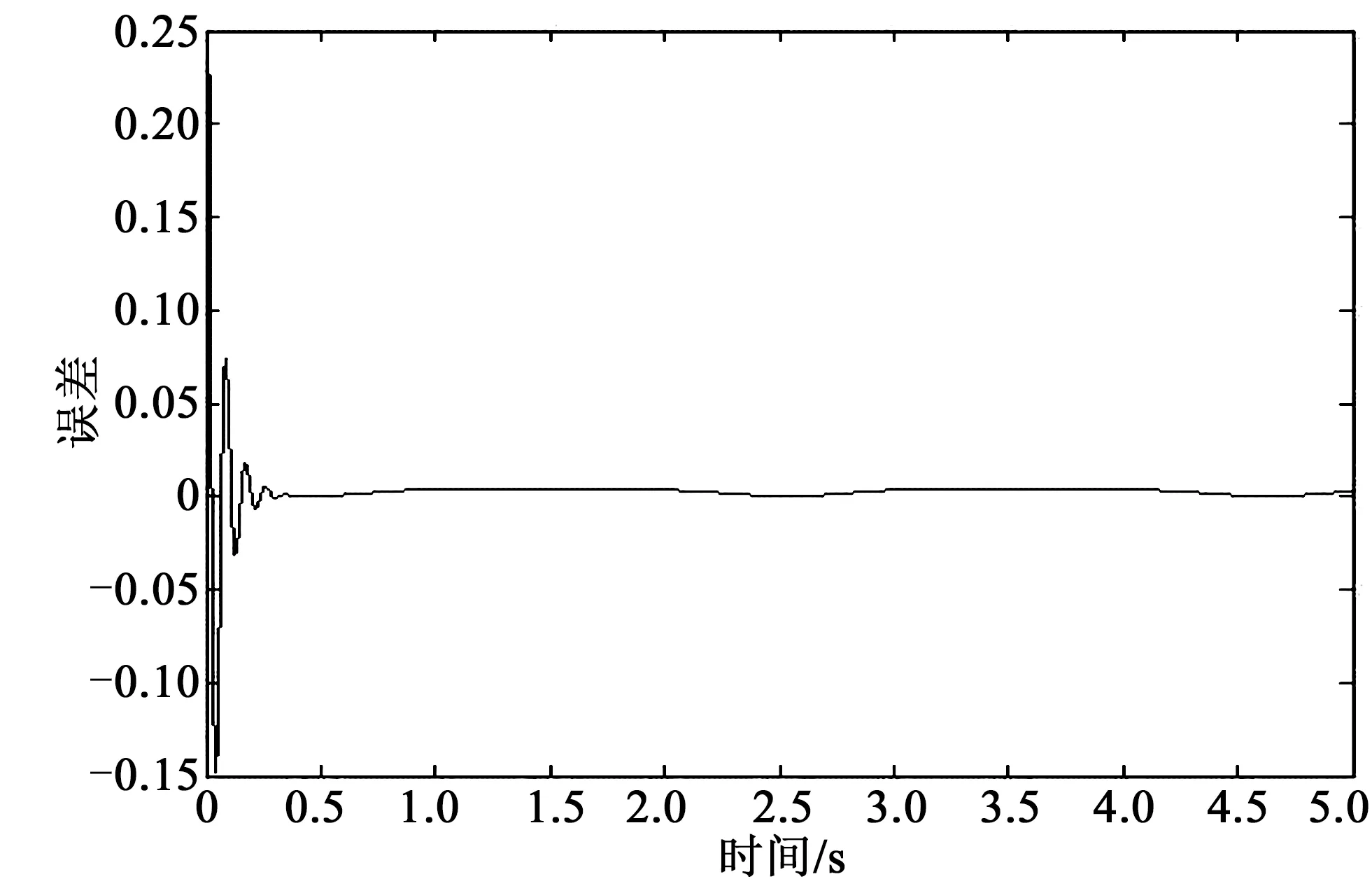
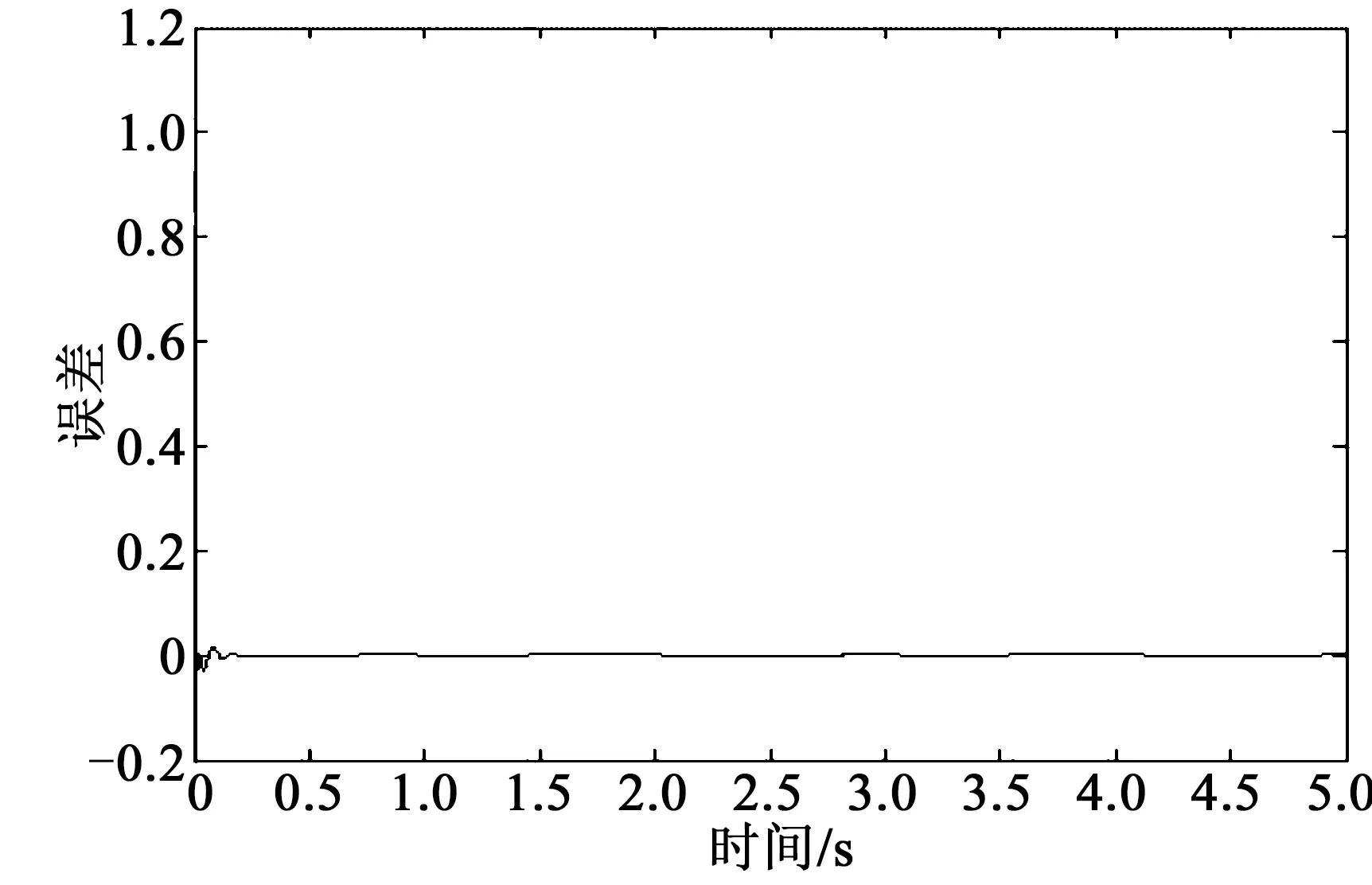
其中,机械臂关节1和2的控制力矩即u1和u2,仿真实验中涉及各参数的标称值为:M1=12.2 kg;M2=11.0 kg;l1=0.35 m;l2=0.24 m;J1=0.49 kg·m2;J2=0.38 kg·m2;|f1| 图2 关节1位置跟踪Fig.2 Joint 1 position tracking 图3 关节2位置跟踪Fig.3 Joint 2 position tracking 图4 关节1跟踪误差曲线Fig.4 Joint 1 tracking error curve 图5 关节2跟踪误差曲线Fig.5 Joint 2 tracking error curve 关节名称位置跟踪误差曲线关节1跟踪曲线超调小,约0.25 s之后进入稳态约0.25 s稳态误差为0,抗干扰能力较强关节2跟踪曲线超调非常小,约0.2 s之后进入稳态约0.2 s稳态误差为0,抗干扰能力较强 仿真过程中控制器各参数初值为:kp1=2 000,kv1=200,ki1=3;kp2=1 800,kv2=200,ki2=5;f0=5。从仿真结果图2~3可以看出,对带有干扰的输入信号,文中所采用的带有前馈补偿的PID控制算法能有效地实现对给定位置信号的跟踪,有较强的鲁棒性。由图4~5可以看出,两关节跟踪误差超调小,到达稳态的时间短,约0.25 s左右即达到稳态。对比图4~5和图6~7可以发现,文中所提出的控制方法与常规PID控制效果相比响应速度快、稳定性强、有较好的鲁棒性,即带有前馈补偿的PID控制方法在系统的跟踪性能方面要优于常规的PID控制。 图6 常规PID控制下关节1跟踪误差曲线Fig.6 Joint 1 tracking error curve under conventional PID control 图7 常规PID控制下关节2跟踪误差曲线Fig.7 Joint 2 tracking error curve under conventional PID control 针对关节机器人系统的轨迹跟踪控制问题,文中采用一种带有前馈补偿的PID控制算法,对带有干扰的给定跟踪信号有效实现了跟踪,关节跟踪超调小,达稳态时间短,有较好的鲁棒性。与常规PID控制方法的比较结果表明,文中所用控制方法能获得较好的静动态特性以及稳定效果。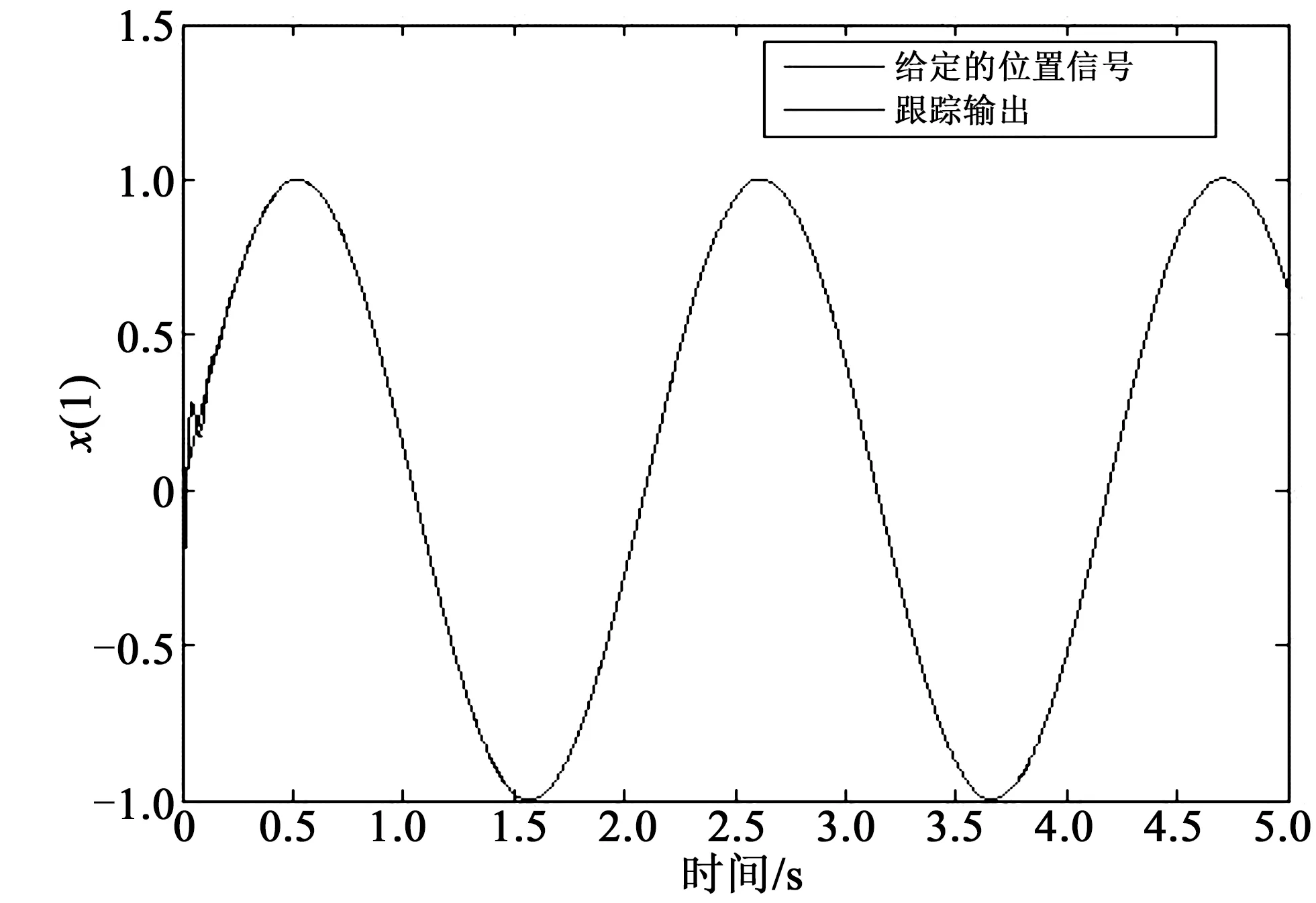

4 结论

