UML类图元模型基于描述逻辑的表示及验证

李晶晶，江 涛，郭雨婷，李 迪，王米利

(云南民族大学数学与计算机科学学院昆明650500)

本文在现有的描述逻辑［1-4］知识表示方法和 UML类图模型形式化表示方法［5-8］的基础上，结合国内外UML类图元模型的相关成果［9-13］，提出一种UML类图元模型基于描述逻辑的表示及验证的方法.该方法在UML类图元模型构建的约束规则集的基础上，可以有效地实现UML类图元模型与其构建模型间的一致性验证问题.但是必须说明的是，正如文献［9-11］中所研究的，本文只是截取了UML类图元模型的一个子集进行表示和验证.

1 描述逻辑SHOIN(D)

1)在描述逻辑SHOIN(D)语言中，概念和属性的语法规则如下［3-4］:

2)语义规则如下［3-4］:

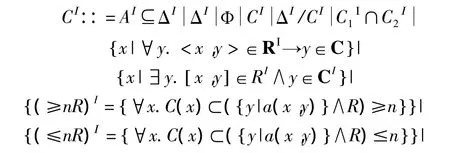
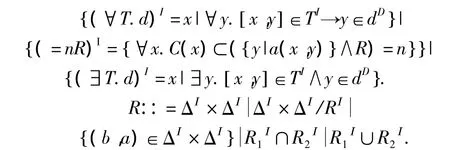
其中，A表示原子概念，C表示复合概念，R和S表示抽象角色，T表示具体角色，D表示抽象数据类型，d表示具体数据类型;┬表示顶层概念，是其他所有概念的父概念;⊥表示底层概念，是矛盾的概念，是所有其他概念的子概念;¬表示否定，∩表示合取(conjunction)，∪表示析取(disjunction)，∃表示存在量词(existential quantification)，∀表示值限定(value restriction)［3］.

2 约束规则集的构建

2.1 UML类图元模型的提取

由于UML类图元模型的庞大性和复杂性，正如文献［9-11］中所研究的，本文只截取UML类图元模型的一个子集进行约束规则集的构建.即对于UML类图元模型，我们忽略一些构造子.但是，这些处理不会对UML类图元模型的语义一致性产生影响.如图1是本文截取的UML类图元模型的一个子集，该UML类图元模型包含 Classifier、Class、property、Operation、Parameter以及类图元模型里面的各种关系.

2.2 约束规则集的构建

在文献［2，5-8］中都已经给出UML类图中基本构造子在描述逻辑SHOIN(D)中的表示.在此，本文直接给出UML类图元模型中的泛化关系和组合关系基于描述逻辑SHOIN(D)的表示.

2.2.1 泛化关系的约束规则

本文只给出 Classifier与 Class、Interface、Signal、Datatype以及Association之间的泛化关系，Relationship与Association和DirectedRelationship之间的泛化关系，以及DirectedRelationship与Generalization、InterfaceRealization、Dependency之间的泛化关系可以类似给出.

1)父类泛化为多个子类.即，父类Classifier可以泛化为子类 Class、Interface、Signal、Datatype 以及Association:

Class⊆Classifier，DataType⊆Classifier，

Interface⊆Classifier，Association⊆Classifier，

Signal⊆Classifier.

2)子类之间的不相交泛化.即，子类Class、Interface、Signal、Datatype 以及 Association 之间互不相交:

Class⊆¬ DataType∩¬ Interface∩¬

Association∩¬ Signal.

DataType⊆¬ Class∩¬ Interface∩¬Association∩¬ Signal.

Interface⊆¬ Class∩¬ DataType∩¬

Association∩¬ Signal.

Association⊆¬ Class∩¬ DataType∩¬

Interface∩¬ Signal.

Signal⊆¬ Class∩¬ DataType∩¬

Interface∩¬ Association.

3)子类之间的完全覆盖泛化.即，子类Class、Interface、Signal、Datatype 以及 Association 将父类Classifier完全覆盖:

Classifier≡Class∪DataType∪Interface∪

Association∪Signal.

2.2.2 组合关系的约束规则

由图1的类图元模型，我们观察到Class、Interface、Signal、Datatype 以及 Association 都有 Property，且它们与Property之间都是组合关系.在此我们规定，对于一个具体的Property(P)，当Property(P)与Class形成组合关系时，Property(P)与Interface、Signal、Datatype以及 Association不形成组合关系.同理，其他也适用.

Property、Operation与Class之间组合关系.即，一个Class可以没有Property和Operation，也可以有多个Property和Operation.同样也适合于Interface、Signal、Datatype以及 Association 中:

Class⊆ (∀ownedAttribute.Property)∩ (≥0ownedAttribute.Property)，

Property⊆(∀class.Class)∩(≥0class.Class)∩(≤1class.Class)Class⊆(∀ownedO peration.Operation)∩(≥0ownedOperation.Operation)，

Operation⊆ (∀class.Class)∩ (=1class.Class).

2.2.3 类的属性的约束规则

1)属性的重数约束规则，如下［7］:

C⊆(≥min a)∩(≤max a).

其中，类C用原子概念C表示，类的属性a用原子关系a表示.注意:属性上，若多重性没有给出，缺省值是 0…*［10］.

2)属性的枚举值约束规则.枚举值表示枚举元类属性的列举值.我们用3条规则来表达枚举元类包含的信息，分别是:枚举值的可区分性、枚举值的类型和枚举元类的完全性.由于用推理机Racer对UML类图元模型进行一致性检测过程中，枚举值的类型和枚举元类的完全性的影响很小，因此本文只对枚举值的可区分性进行描述.

枚举值的可区分性规则用SHOIN(D)表示如下:

其中，原子概念A1和A2分别对应于枚举值a和b.

由图1的类图元模型，枚举元类ParameterDirectionKind定义了 4个枚举值 in，out，inout和 return.对ParameterDirectionKind的可区分性用SHOIN(D)描述如下.

in⊆¬ out，in⊆¬ inout，in⊆¬ return，…，

return⊆¬ inout.

in⊆¬ out∪¬ inout∪¬ return.

out⊆¬ in∪¬ inout∪¬ return.

inout⊆¬ in∪¬ out∪¬ return.

return⊆¬ in∪¬ out∪¬ inout.

2.2.4 关联关系的约束规则

1)关联关系的类型约束规则.对由C1到C2之间含有类型A的二元关联，约束规则如下(如图2所示):A⊆C1∩C2.即，对于从A导出的二元关系A，若第1个参数是以C1为类型的元素，则第2个参数必须以C2为类型.

2)关联关系的多重性约束规则.对由C1到C1且带有多重性M的二元关联A，根据M的不同情况，给出以下形式的规则(如图2所示):

C1⊆(≥min A.C2)∩(≤max A.C2);C2⊆(≥min A-.C1)∩(≤max A-.C1).

注意:关联端点上没有给出多重性，意味着多重性是 1［10］.

3)带角色关联的多重性约束规则.对由C1到C2的二元关联A，令R1是A在C1端的端点名，R2是A在C2端的端点名，M1是R1上的重数，M2是R2上的重数(其中 M1、M2均有 min、max)，则有如下规则(如图3所示):

A⊆R1∩R2∩∃R1.C1∩∃R2.C2，

C1⊆(≥min R2.C2)∩(≤max R2.C2)，

C2⊆(≥min R1.C1)∩(≤max R1.C1).

其中，在关联关系A中，定义域概念C1实例的重数大于最小值min，小于最大值max;值域概念C2实例的重数大于最小值min，小于最大值max.

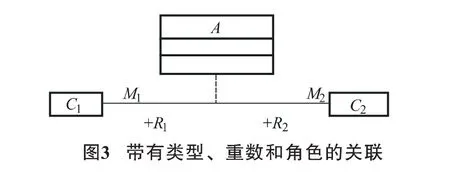
由图1的类图元模型，Association与Property之间的关联关系是一种带角色和多重性的关联关系，具体表示如下:

Association⊆≥2memberEnd.Property，

Property⊆(≥0association.Association)∪(≤1association.Association).

即关联关系可以有关联角色和多重性，且当关联角色确定以后，关联关系两端的类唯一确定.

其他关联关系之间的规则同上.

3 一致性验证

3.1 相关定义

在文献［13］的基础上给出以下定义:

定义1:类图元模型的逻辑一致性.如果一个类图元模型的约束规则集Lx是逻辑一致的，形式化地说，类图元模型的约束规则集Lx中的每个关系式在推理机Racer中都不存在矛盾，则我们称类图元模型是逻辑一致的;反之，如果一个类图元模型的约束规则集Lx是逻辑不一致的，形式化地说，类图元模型的约束规则集Lx中的关系式之间在推理机Racer中存在矛盾，则我们称类图元模型是逻辑不一致的.

由于手工推理的复杂性，在此，我们借助推理机Racer来对UML类图元模型进行一致性的验证.将UML类图元模型的约束规则集放入Racer里面，经验证UML类图元模型是逻辑一致的.

定义2:类图模型—元模型间的逻辑一致性.如果一个类图模型满足类图元模型，形式化地说，类图模型对应的结构语义集L1在推理机Racer中满足类图元模型的约束规则集Lx，则我们称类图模型对应于类图元模型是逻辑一致的;反之，如果一个类图模型不满足类图元模型，形式化地说，类图模型对应的结构语义集L1在推理机Racer中存在不满足类图元模型的约束规则集Lx，则我们称类图模型对应于类图元模型是逻辑不一致的.

其中，L1表示类图模型基于描述逻辑SHOIN(D)的结构语义集，Lx表示类图元模型基于描述逻辑SHOIN(D)的约束规则集.

3.2 模型研究

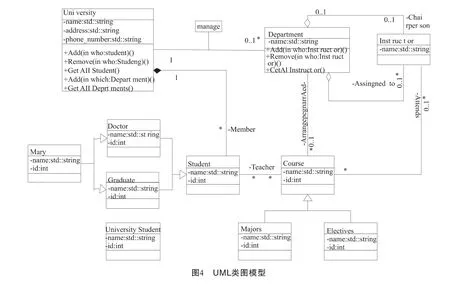
在此，我们借助推理机Racer对UML类图模型进行一致性的验证.将UML类图元模型的约束规则集和UML类图模型的结构语义集放入Racer里面.经验证，UML类图模型里面存在以下矛盾:

1)Student与Doctor和Graduate之间的泛化关系违背了子类的完全覆盖泛化规则.

众所周知，University里面的Student一定包含UniversityStudent.即，一定存在

Class(Universitystudent)⊆Class(Student).

而图4中的UML类图模型里面的Student只包含Doctor和Graduate.即，只存在

Class(Doctor)⊆Class(Student)，

Class(Graduate)⊆Class(Student).

2)Mary与Doctor和Graduate之间的泛化关系违背了子类的不相交泛化规则.

作为一名具体的学生类Mary，她即是Doctor又是Graduate.即，下列结构语义同时存在

Class(Mary)⊆Class(Doctor)，

Class(Mary)⊆Class(Graduate).

这在类图里面是不允许的，且与现实情况不相符.

3)Student与Course以及Course与Instructor之间的关联关系均违背了关联关系的类型约束规则.

Student与Course之间是Attends的关系，Course与Instructor之间是 Teacher的关系.而图4中的UML类图模型得到的结构语义规则与之正好相反.

Association(Teacher)⊆Class(Student)∩Class(Course)，

Association(Attends)⊆Class(Course)∩Class(Instructor).

由上述验证结果可知，该UML类图模型对应于UML类图元模型是逻辑不一致的.

4 结语

本文针对UML类图元模型的非形式化表示方法，在深入分析UML类图模型形式化表示及提取UML类图元模型的一个子集的基础上，构建了UML类图元模型基于描述逻辑SHOIN(D)的约束规则集，并借助推理工具Racer验证了UML类图元模型与其构建模型之间的一致性.下一步的工作包括不断完善UML类图元模型的约束规则集、开发一种软件来实现UML类图元模型的自动推理引擎以及对UML类图模型的自动形式化描述与一致性验证功能.

［1］Object Management Group.OMG final adopted specification［EB/OL］.［2006-8-23］http://www.omg.org/bpmn/Documents/OMG_Final_Adopted_BPMN_1-0_Spec_06-02-01.Pdf.

［2］吴建，郑潮，汪杰.UML基础与Rose建模案例［M］.北京:人民邮电出版社，2004.

［3］BAADER F，NUTT W.Basic description logic［M］.Cambridge，UK:Cambridge University Press，2003.

［4］ROSSI F，BEEK P，WALSH T.Handbook of Constraint Programming［M］.Amsterdam:Elsevier，2006.

［5］郝斐，董庆超，曾广军.一种基于描述逻辑的UML模型验证方法［J］.计算机与数字工程，2011(11):58-62.

［6］齐玉东，杨斌，李瑛，等.基于描述逻辑的Onto UML模型的形式化表示［J］.计算机工程与科学，2012(7):89-92.

［7］董庆超，王智学，张爱辉，等.基于UML类图模型的一致性检查方法［J］.计算机技术与发展，2008(10):85-88.

［8］陈振庆.基于SHOIN(D)的UML类图形式化方法［J］.计算机工程与科学，2009(19):43-45.

［9］单黎君，朱鸿.UML的形式化描述语义［J］.计算机工程与科学，2010(3):96-103.

［10］单黎君.图形的一致性检查［D］.长沙:国防科学技术大学，2008.

［11］BERARDI D，CALVANESE D，GIACOMO G.Reasoning on UML class diagrams［J］.Artificial Intelligence，2005，168(3):70-118.

［12］沈国华，张伟，黄志球，等.基于描述逻辑的特征语义建模及验证［J］.计算机研究与发展，2013(7):1501-1512.

［13］JIANG Tao，WANG Xin.Research on meta-models consistency verification based on formalization of domainspecific metamodeling language［J］.上海交通大学学报:英文版，2012，17(2):171-177.