立方晶格晶面间距的计算

屈 盛，杨留方，刘涵哲，马雄韬，王玉林

(云南民族大学电气信息工程学院，云南昆明650500)

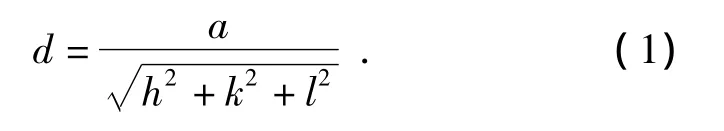
晶面间距是固体物理学中的一个很重要的参数，研究晶体结构时往往会用到它.在《X射线衍射分析》和《材料科学》的不少教材中常常采用下式来计算立方晶格的晶面间距［1－3］:式中，a为立方系晶胞(单胞)的边长(即晶格常数)，而(hkl)是晶面的密勒指数，d为相应的晶面间距.在教学实践中常常看到，在计算简单立方晶格的晶面间距时，(1)式是正确无误的，但在计算面心立方(FCC)晶格和体心立方(BCC)晶格的晶面间距时，(1)式所得出的结果有时是错误的.例如，利用(1)式计算 FCC晶格的(100)面和(111)面的晶面间距时，所得的结果分别为 a和 a/，即(1)式可以得出(100)面的晶面间距大于(111)面的晶面间距的结论.但由晶体学知识我们知道，FCC晶格中(111)面为最密排面，其晶面间距应该是所有晶面族中最大的.(1)式计算所得的结果与这个常识相矛盾，可见(1)式并不适用于 FCC晶格晶面间距的计算.

文献［4］中指出了上述矛盾和(1)式的局限性，然而作者通过计算却得出FCC晶格中(100)面和(111)面的晶面间距是相等的(均为a/).这显然是错误的，因为FCC晶格中，(100)面和(111)面上的原子排列情况并不相同，(111)面是最密排面，而(100)面并不是最密排面，所以二者的晶面间距理应是不相同的.鉴于教材和文献中对于晶面间距的计算(尤其是对于立方晶格的晶面间距的计算)，过于笼统和不精确，本文对晶面间距的计算进行了深入的总结与讨论，并给出一种利用密度比来计算晶面间距的方法，最后利用这些方法分别计算了FCC晶格和BCC晶格的晶面间距.如果不同方法的计算结果是完全相同的，则可以验证这些计算方法都是正确的.

1 晶面间距的传统计算方法

1.1 以原胞基矢描述的计算

在有关教材中，常常采用2种基本的重复单元来描述晶格的周期性和对称性［5－6］:一种是固体物理学原胞，另一种是晶体学单胞(也称晶胞).对于布喇菲格子来说，原胞只在其顶角处存在原子，而晶胞则在其顶角、面心、体心、底心处均可以存在原子［5－7］.因此，原胞和晶胞并不完全相同，只有简单布喇菲格子(例如简单立方、简单四方、简单正交等晶格)的晶胞才和它的原胞相同.参照文献中的习惯，为了便于区别，本文也将原胞的基矢记为a1、a2和a3，对应的晶面的参数记为(h1h2h3)，称之为面指数;而将晶胞的基矢记为a、b和c，对应的晶面的参数记为(hkl)，称之为密勒指数［7］.利用倒格矢的性质可以知道，(h1h2h3)晶面族的晶面间距可以由下式计算得到［7－9］:

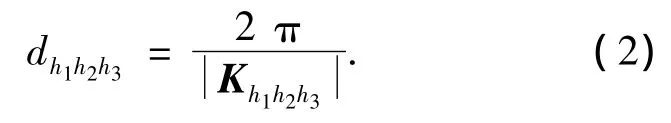
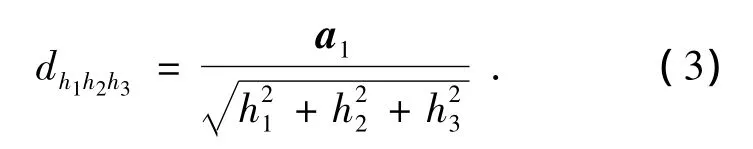
实际工作中，常常用密勒指数(hkl)来表征晶面，而不是用面指数(h1h2h3)来表征晶面.由于晶胞的基矢 a、b、c和原胞的基矢 a1、a2、a3并不一定全同，因而对于同一族晶面，其密勒指数(hkl)与面指数(h1h2h3)并不一定相同，而(hkl)和(h1h2h3)相同，也并不一定表示同一晶面族［7］.所以，(2)式和(3)式并没有直接给出以(hkl)标记的晶面族的晶面间距［7］.因此，对于实际工作来说，(2)式和(3)式的使用很有限，必须找出利用密勒指数(hkl)来表示的晶面间距dhkl的公式［8］.

1.2 以单胞(晶胞)基矢描述的计算

根据文献［8］，利用密勒指数(hkl)表示的晶面间距dhkl的计算公式可以归纳为［8］:

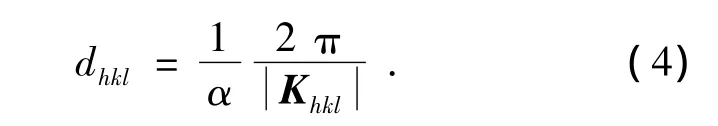
其中，Khkl=ha*+kb*+lc*为倒格式，而a*、b*、c*为倒格子基矢，而α=1或者2，是与结构有关的系数.

对于立方系布喇菲格子，由于a=b=c，故晶面间距可表示为:

由文献［7－8］可知，对于简单立方晶格，α恒等于1;而对于面心立方晶格，当h、k、l均为奇数时α等于1，否则α等于2;对于体心立方晶格，当h+k+l=偶数时α等于1;否则α等于2.也就是说，面心立方晶格的晶面间距的计算公式为［7－10］:

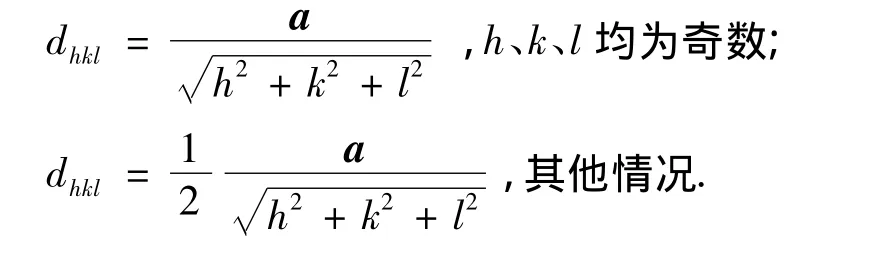
而体心立方晶格的晶面间距的计算公式为［7，10］:

显然，(5)式比(1)式更能准确地反映出立方晶系(hkl)晶面族的晶面间距，(1)式只是(5)式在特定情况下的形式，或者说，(1)式只适合于计算简单立方晶格的晶面间距，这就是本文开始部分中所提到的矛盾所产生的原因.

需要指出的是，(5)式简化为(1)式的晶面条件和面心(体心)立方晶格产生X线的衍射的晶面条件相同，例如，计算面心立方(111)面的晶面间距时，由于此时满足h、k、l均为奇数的条件，故(5)式简化成了(1)式，而此时该结构的(111)晶面恰好也是对X线产生衍射的晶面.

2 晶面间距的密度比的计算方法

2.1 密度比的计算方法

如果将晶格中单位面积内所包含的原子数目定义为面密度σ，而将单位体积内所包含的原子数目定义为体密度ρ，则可以利用下式来计算晶格的晶面间距:

2.2 FCC和BCC的晶面间距的计算

图1给出FCC和BCC晶格的不同晶面上的原子排布情况，表1则给出了对应的不同晶面上的三角形或四边形的面积、所含原子数目、计算得到的面密度、晶格的体密度和按照(6)式计算得到的晶面间距.表1的最后一列还给出了由(5)式计算得到的结果.由表1可以看到，(6)式的计算结果和(5)式的计算结果完全一致，因此两式可以相互验证对方的正确性.

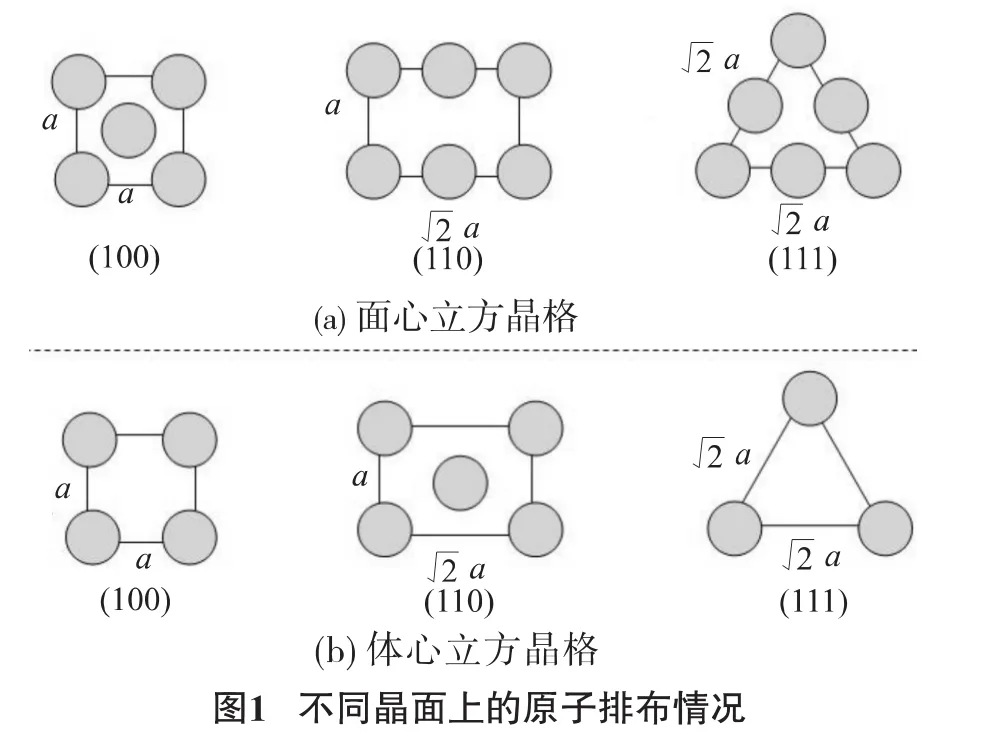
利用(6)式计算晶面间距时，应注意体密度和面密度的计算要正确.计算体密度时往往取一个晶胞来计算.例如一个体心立方晶胞和一个面心立方晶胞的体积均为a3，且分别含有2个原子和4个原子，因此体心立方晶格和面心立方晶格的体密度分别为2/a3和4/a3.而计算面密度时则稍微复杂些.例如一个体心立方晶胞和一个面心立方晶胞的(100)面的面积均为a2，且分别含有1个原子和2个原子，如图1所示，因此，体心立方晶格和面心立方晶格(100)面的面密度分别为1/a2和2/a2.故由(6)式计算得到的体心立方晶格和面心立方晶格(100)面的晶面间距均为a/2.

由上面的计算还可以知道，利用(6)式计算晶面间距比利用(5)式计算要复杂一些.但是(6)式没有使用条件，可以应用于任何一个晶面族的计算，而(5)式应用于不同晶面族的计算时，系数α有所不同，如果记不住其使用条件，那么有可能会计算错误.

3 结语

文中的(1)式并不能正确地计算所有立方晶格的晶面间距，在计算面心立方晶格和体心立方晶格的晶面间距时，应该使用(5)式来计算或者采用本文给出的(6)式来进行计算，(1)式只是(5)式在特定情况下的形式.从本文的例子可以看到，(5)式和(6)式的计算结果是一致的，它们可以相互验证对方的正确性.

表1 利用密度比的方法来计算FCC和BCC的晶面间距时所得到的结果

［1］黄胜涛.固体X射线学［M］.北京:高等教育出版社，1985:33－35.

［2］陈建，严文，刘春霞.材料研究方法［M］.北京:化学工业出版社，2011:47－48.

［3］石德珂.材料科学基础［M］.北京:机械工业出版社，2003:43－44.

［4］马天平，谭伟石.由面心立方(111)面间距谈几何晶体学的几个基本概念［J］.物理通报，2012(2):15－17.

［5］黄昆，韩汝琦.固体物理学［M］.北京:高等教育出版社，1988:6－11.

［6］方俊鑫，陆栋.固体物理学(上册)［M］.上海:上海科学技术出版社，1980:13－31.

［7］吴英凯.以密勒指数(hkl)标志的晶面族面间距公式［J］.大学物理，1991(10):7－14.

［8］冯家显.面间距公式的一点探讨［J］.浙江师范大学学报:自然科学版，1989，12(2):84 －89.

［9］冯双久，张晓红.有心立方晶格面间距的计算［J］.大学物理，2005，24(9):33 －34.

［10］宫秀敏，朱勇，周一志.关于FCC和BCC点阵晶面间距计算式的证明［J］.武汉工学院学报，1991，13(1):51－57.