基于随机森林法的煤矿微震危害预测

李 盛，郭民之，康文倩

(云南师范大学数学学院，昆明650500)

微震灾害是最难探测和预测的自然灾害之一，越来越多的先进的微震预警系统使我们更好的了解岩体运动过程和微震灾害预测方法的定义，然而到目前为止很多方法的准确性不尽如人意.在很多高能量(大于10 000 J)微震事件中，由于微震过程的复杂性和不均衡性导致统计技术不足以预测微震灾害.因此，有必要寻找更好的方法预测微震灾害，使用机器学习方法就是一种途径.Lesniak，Isakow［1］用数据聚类技术评估微震灾害和Kabiesz［2］使用人工神经网络对微震灾害预测都有一定效果.在许多文献中，提到的方法以“危险”和“无危险”两种状态形式呈现，正数(危险状态)和负数(无危险状态)的不平衡分布是微震灾害预测中的一个严重问题，当前使用的方法不足以使预测达到良好的敏感性和特异性.Kijko［3］使用非参数方法对矿山微震灾害进行分析，Sikora［4］用归纳和修剪的分类规则预测煤矿微震的危害，这两种方法所取得的效果不是太理想.Bukowska［5］在其论文中提出在发生微震时能量大于10 000 J情况下，在众多因数中，有一些因数影响微震灾害的发生.微震预测可以用不同的方式来定义，但主要目的都是预测微震活动可导致岩爆的精确日期和时间.

煤矿矿震危险性预测的方法主要有:模糊聚类法和神经网络算法，但模糊聚类法在确定分类指标权值时，存在一定的主观性，而传统的神经网络算法都是基于大样本数据的，推广性较差.基于随机森林分类原理的预测方法有不需要对数据预处理，能有效的解决不平衡、高维分类问题，能较好的容忍噪声并且不会过拟合，分类结果稳定等优点.矿震危险性预测是一个非线性、高维的多类模式识别问题，随机森林方法更适合解决这类模式识别问题.因此，本文提出了一种基于随机森林法的煤矿微震危险性预测方法.

1 随机森林法原理及性质

1.1 原理

随机森林法(random forests)是 Breiman［6］于2001年提出的一种新的组合分类器算法.随机森林分类是由很多决策树分类模型{h(x，θk)，k=1，2，…}组成的组合分类模型，参数集{θk}是独立同分布的随机向量，在给定自变量x下，每个决策树分类模型都由一票投票权来选择最优的分类结果.利用Bootstrap抽样从原始训练集抽取k个样本，每个样本的样本容量均与原始训练集一样，对k个样本分别建立k个决策树模型，得到k种分类结果.根据k种分类结果对每个记录进行投票表决决定其最终分类，如图1.

随机森林法通过构造不同的训练集增加分类模型的差异，以提高组合分类模型的外推预测能力.通过k轮训练，得到分类模型序列{h1(x)，h2(x)，…，hk(x)}，再用它们构成多分类模型系统，该系统的最终分类结果采用简单多数投票法，最终的分类决策为:

其中，h(x)表示组合分类模型，hi是单个决策树分类模型，y表示输出变量，I(·)为示性函数.公式(1)表明使用多数投票决策的方式来确定最终的分类.

1.2 随机森林算法

在分类回归树(CART)算法中，每个内部节点都是原始数据集的子集，根节点包含了所有的原始数据.在每个内部节点处，从所有属性中找出最好的分裂方式进行分裂，再对后续节点依次进行分裂，直到叶节点，最后通过剪枝使测试误差最小.而随机森林法与算法有所不同，单棵树的生长可归纳为以下3点:

1)用Bagging方法形成新的训练集:在样本数为N的原始训练集中，有放回地随机选取N个样本形成一个新的训练集，以此生成一棵分类树;

2)随机选取特征对分类回归树的内部节点进行分裂:设共有 M个特征，取任意正整数 m，且m≪M.对于每个内部节点，从M个特征中随机抽取m个特征作为候选特征，选择这m个特征上最好的分裂方式对节点进行分裂;

3)每棵树自由生长，不进行剪枝.

1.3 随机森林的泛化误差

泛化误差的大小可以衡量分类器的性能，泛化误差越小，则分类器的性能越好，反之则性能越差.给定分类器 h1，h2(x)，…，hk(x)，对于输入变量 x和输出变量y，定义边缘函数为:其中I(·)为示性函数，avk(·)为取平均数.边缘函数衡量给定的分类器集合将输入变量x分到正确类别的平均票数，与分到其他类别的平均票数的最小差值，因此边缘函数值越大，分类的可信度就越高，分类器的泛化误差表示为 PE*=Px，y(mg(x，y)＜0).

当随机森林中树的棵数足够多时，根据大数定律我们可以得到:随着森林中树的棵数增加，对于序列，几乎处处收敛于

公式(3)表明当随机森林中树的棵数增加时，不会发生过拟合，并得到一个有限的泛化误差值.随机森林的泛化误差上界由给出，其中，s表示单棵树的分类性能，¯ρ表示树与树之间的相关性.由此可知，单棵树的分类性能越好，树与树之间的相关度越低，随机森林的泛化误差上界越小.

2 标准化均方误差(NMSE)

采用五折交叉验证的方法来判断各种机器学习方法结果的可靠性.计算中通过随机建立的5个训练集建立5个模型，对训练集和测试集分别得到5个标准化均方误差(NMSE)，再得出5次平均的NMSE.令为因变量均值，为从训练集得到的模型对一个数据集(可能是训练集本身也可能是测试集)的预测值，这里的NMSE定义为:

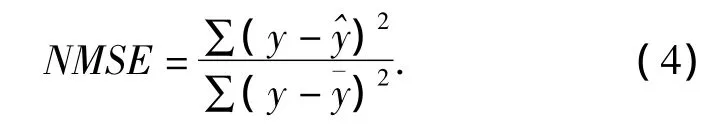
显然，如果什么模型都不用，只用均值来做预测，那么 NMSE等于1.所以，如果在回归时得到NMSE大于1，这个模型就很糟糕了，还不如没有模型.仅仅对于训练集来说，其NMSE等于1－R2，R2为回归系数.但是对于测试集来说，其NMSE与测试集的R2没有什么关系.

3 算例

3.1 样本选取

本文数据来自UCI机器学习数据库中的seismic－bumps数据集，数据来自位于波兰的采用长壁开采法的煤矿每8 h监测一次的实时数据.数据集描述在高能量(大于104J)情况下关于煤矿开采微震灾害的预测问题，数据集包括2 584个样本，9个自变量，其中包括2种微震危害评估方法［7］x1、x2(a表示不危险，b表示低危险，c表示高危险，d表示危险状态)，x3(W表示继续工作，N表示准备转移)，x4为由微震检波器检测到的能量，x5为检测到的脉冲，x6为当前记录能量与先前8次记录能量的平均的偏差，x7为当前记录脉冲与先前8次记录脉冲的平均的偏差，x8为上一次转移登记能量值的总和，x9为上一次转移登记的最大能量值.一个因变量(y)，即危险级别，1表示下一次转移是高能量颤动(危险状态)，0表示下一次转移不是高能量颤动(无危险状态)，其中有167个正数1.使用R软件对数据集进行分析［8－9］.

表1 数据集变量

3.2 数据分析

数据集描述在高能量(大于104J)情况下关于煤矿开采微震灾害的预测问题，通过已有数据自身特点的分类分析，预测下一次高能量颤动采取的策略:“1”表示将有高能量震动(危险状态)，“0”表示接下来无高能量震动(无危险状态)，其中有167个正数1，占总数据的6.5%.数据集中所测能量大于104J的样本有2 035个，占总数据的78.8%，在高能量颤动发生时采取转移的样本占高能量样本的8.2%，数据的部分特征见表2.

表2 微震能量大于104J的数据总结

上表可以看出是否转移与高能量颤动的发生是密切相关，但不是只要是高能量发生就必须要转移.因为微震过程既包含线性的关系，也包含了复杂的非线性关系，所以分析数据集各变量之间是否具有线性关系.由图2可以看出因变量与各自变量间不存在明显的线性相关性，线性模型在分析多样本、高维度的高能量煤矿矿山微震数据效果不好.

下面对危险评估方法进行分析，选取危险级别为“1”的样本集和紧接危险级为“1”后的一个样本构成的样本集为分析对象，通过对微震危害评估方法分析，发现seismic评估方法对紧接危险级“1”后的一个样本评估比seismoacoustic评估方法好点，但都不能准确地预测微震灾害.

表3 危险评估方法与危险级别的比例分析

用传统的线性模型很难分析多变量、不平衡分布的微震数据，故提出机器学习方法，机器学习方法对数据没有任何假定，产生的结果用交叉验证的方法来判断，脱离了假定分布⇒假设检验⇒p值的经典统计过程。这种基于算法或程序的模型预测效果相当好，而且交叉验证的结果也容易被广大实际工作者所理解和接受.

表4给出了随机森林方法对数据集的NMES分析结果，并与决策树、Bagging算法、支持向量机(SVM)和最近邻法所得到的NMSE结果进行比较，发现这几种机器学习方法对数据集分析效果都较好，其中随机森林方法对数据集构造的训练集和测试集的为9.67×10－5和0.067 33，是上述方法中结果最理想的，说明随机森林方法在处理高能量煤矿矿山微震数据时能很好的控制误差.

表4 几种机器学习方法对数据集的NMSE分析

表5 几种机器学习方法对数据集的预测精度分析

对数据集做预测精度分析，先把数据分成E≥105J数据、E≥104J数据、E＜104J数据和整个数据4个样本集，用表5中的机器学习方法对各个样本集做预测精度分析，上述方法对危险级为“0”的样本的预测都较理想，预测精度都在90%以上，对危险级为“1”的样本的预测较差，可能由其样本数在总样本数中占的比例较小的缘故.其中，E≥105J的样本的预测结果较其他样本集的结果好，说明高能量的检测与微震的发生是紧密相关的.随机森林方法对数据的预测分析效果最理想.

4 结语

在煤矿开采中微震引发的一系列监测数据可以描述为时间系列，其中既包含线性的关系，也包含了复杂的非线性关系，微震过程的复杂性和不均衡性

导致线性模型不足以预测微震灾害.本文注重采用机器学习方法分析在高能量(大于)情况下关于煤矿开采微震灾害的预测问题，发现随机森林法、决策树、Bagging算法、随机森林、支持向量机和最近邻方法对处理高能量微震数据都具有较好的误差容忍性，其中随机森林法的五折交叉验证的值都较低，能很好的控制误差，在对高能量煤矿矿山微震预测分析时，随机森林法效果最理想.本文的不足之处是没能结合国内的煤矿矿山微震数据进行比较分析.

［1］LE S＇NIAK A，ISAKOW Z.Space-time clustering of seismic events and hazard assessment in the Zabrze-Bielszowice coal mine，Poland［J］.International Journal of Rock Mechanics and Mining Sciences，2009，46(5):918－928.

［2］KABIESZ J.Effect of the form of data on the quality ofmine tremors hazard forecasting using neural networks［J］.Geotechnical and Geological Engineering，2006，24(5):1131－1147.

［3］KIJKO A，LASOCKI S，GRAHAM G.Non－parametric seismic hazard in mines［J］.Pure and Applied Geophysics，2001，158(9/10):1655 －1675.

［4］SIKORA M.Induction and pruning of classification rules for prediction of microseismic hazards in coal mines［J］.Expert Systems with Applications，2011，38(6):6748－6758.

［5］BUKOWSKA M.The probability of rockburst occurrence in the Upper Silesian Coal Basin area dependent on natural mining conditions［J］.Journal of Mining Science，2006，42(6):570－577.

［6］BREIMAN L.Random forests［J］.Machine Learning，2001，45(1):5－32.

［7］BARANSKI A，DRZEWIECKI J，KABIESZ J，et al.Rules of application of the comprehensive and detailed rockburst hazard assessment methods in hard － coal mines［J］.Expert Systems with Applications:An International Journal，2011，38(6):6748 －6758.

［8］吴喜之.复制数据统计方法——基于R的应用［M］.北京:中国人民大学出版社，2012.

［9］吴喜之.统计学:从数据到结论［M］.北京:中国统计出版社，2013.