关于(m，n)－凝聚环

龚志伟

(福建农林大学 计算机与信息学院，福建 福州 350002)

0 引言

本文总设环为有单位元的结合环，模均为酉模，用pd，fd表示模的投射维数，平坦维数。其余未指明的定义和符号可参见文献［1］和［2］。

1984年 Ng.H.K.在文［3］定义并研究了模的有限表现维数(f.p.dim)的概念，它度量了一个模为有限表现模的程度.1989年丁南庆教授在文［4］中定义了M的有限生成维数f.g.d(M)，它度量了模M为有限生成模的程度。作为推广，在文［5］中研究了模的n－表现维数FPnd(M)。它度量了一个模M为n－表现模的程度。

作为n－表现维数的应用，本文利用n－表现维数引进了(m，n)－内射模及(m，n)－平坦模的概念，讨论了它们的性质，并引进了右(m，n)－凝聚环的概念，给出了右(m，n)－凝聚环的若干刻画。

预备知识:

定义1.1 设M为右R－模，定义M的n－表现维数为

其中 Pm，…，Pm+n是有限生成的}。

若无上述分解存在，则定义FPnd(M)=∞。

显然，FP0d(M)即为文［4］中的有限生成维数f.g.d(M)，FP1d(M)即为文［3］中的有限表现维数f.p.d(M)。由定义1.1 知，M 是n － 表现模当且仅当FPnd(M)=0。

1 (m，n)－内射模与(m，n)－平坦模

定义2.1(1)设m，n是非负整数，M为右R－模，若对任意右 R－模 P，且FPnd(P)=m，都有(P，M)=0，则称 M 是(m，n)－内射的。

(2)设m，n是非负整数，M为右R－模，若对任意左R－模 Q，且 FPnd(Q)=m，都有(M，Q)=0，则称M是(m，n)－平坦的。(m，n)－内射左R－模和(m，n)－平坦左R－模可类似的定义。

显然，右R－模M 是(0，n)－内射的((0，n)－平坦的)当且仅当它是n－FP－内射的(n－平坦的)。

命题 2.2 设{Mi}i∈Ⅰ是右 R － 模集，m，n 是非负整数，则

(1)⊕ⅠMi是(m，n)－平坦的当且仅当每个Mi是(m，n)－平坦的。

(2)ⅡⅠMi是(m，n)－内射的当且仅当每个Mi是(m，n)－内射的。

命题2.3 M是(m，n)－平坦右R－模当且仅当M*是(m，n)－内射左R－模。

命题2.4(1)(m，n)－平坦模的纯子模是(m，n)－平坦的。

(2)(m，n)－内射模的纯子模是(m，n)－内射的。

证明(1)设M是(m，n)－平坦模，N是M的纯子模，则由纯正合列

可知，有可列正合列

由命题2.3可知M*是(m，n)－内射的，从而由命题2.2可知N*是(m，n)－内射的，又由命题2.3可知N是(m，n)－平坦的。

(2)设N是(m，n)－内射模M的纯子模，且FPnd(P)=m，则存在投射分解

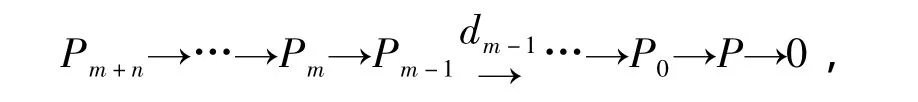
其中Pm，…，Pm+n是有限生成的。令 K=kerdm－1，则K 是n－表现的。因为(K，M)≅(P，M)=0，所以由文［6，命题 2.6］可知，(P，N)≅(K，N)=0.即N 是(m，n)－内射的。

2 (m，n)－凝聚环的刻画

定义3.1 环R称为右(m，n)－凝聚环，如果对于每个n－表现维数为m的右R－模P均有FPnd(P)=FPn+1d(P).

定理3.2 设R是环，m，n是非负整数，则下列叙述等价.

(1)R是右(m，n)－凝聚环。

(2)对任意左R － 模集{Mi}i∈Ⅰ和右R－模P，且FPnd(P)=m，都有(P，ⅡⅠMi)≅(P，Mi)。

(3)(m，n)－平坦左R－模的任意直积是(m，n)－平坦的。

(4)RR的任意直积是(m，n)－平坦的。

(5)对任意右R－模正向系(Mi)Ⅰ和右R－模P，且FPnd(P)=m，都有Extm+n(P，Mi)≅Extm+n(P，Mi).

(6)任意(m，n)－内射模的正向极限是(m，n)－内射的。

(8)对任意的右R－模M，M是(m，n)－内射的当且仅当M*是(m，n)－平坦的。

(9)对任意的右R－模M，M是(m，n)－内射的当且仅当M＊＊是(m，n)－内射的。

(10)对任意的左R－模U，U是(m，n)－平坦的当且仅当U＊＊是(m，n)－平坦的。

证明(1) ⇒(2).设 FPnd(P)=m，因为 R是右(m，n)－凝聚环，所以FPn+1d(P)=m，从而有投射分解

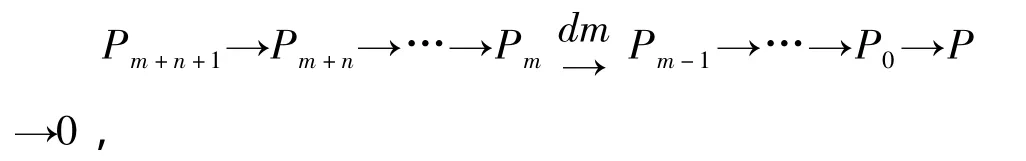
其中Pm，…，Pm+n+1是有限生成的。设Ki=kerdi，则Km+n－1是有限表现的。由于对于任意左R－模集{Mi}i∈Ⅰ，有如下的行正合交换图，

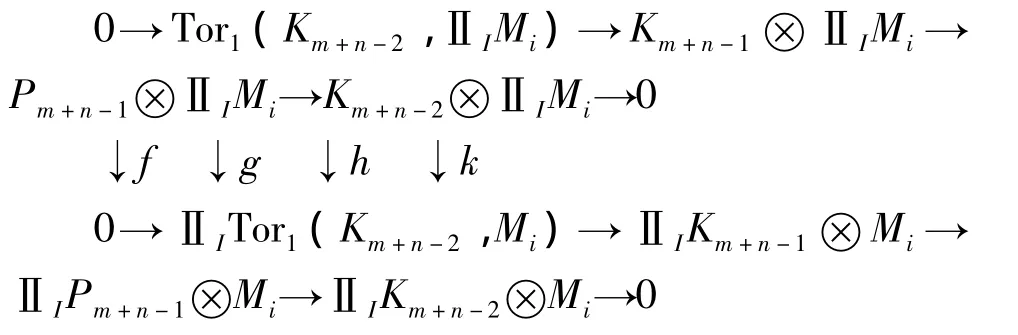
因为 Km+n－1，Pm+n－1是有限表现的，所以由［7，命题5.11］可知 g，h同构，从而f也是同构的。因此，

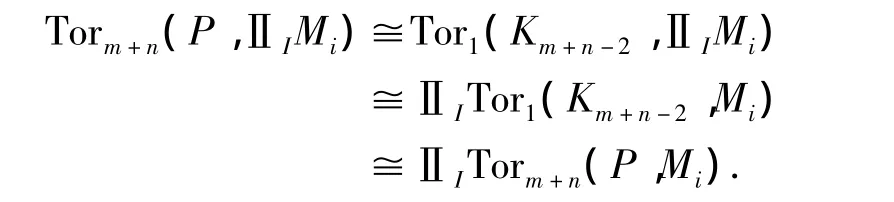
(2)⇒(3)⇒(4)是显然的。

(4)⇒(1).对于给定的模P，且FPnd(P)=m，则在上面交换图中 Km+n－1是有限表现的。设 Mi=RR，由(4)有

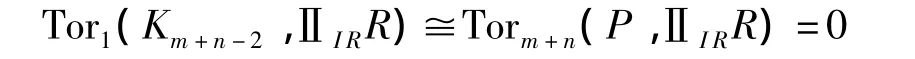
又由［7，命题5.11］可知 h，k同构，因此 g是同构的，又由［7，命题5.11］可知 Km+n是有限表现的，因此FPn+1d(P)≤m，又因为m=FPnd(P)≤FPn+1d(P)，所以 FPnd(P)=FPn+1d(P)，故 R 是右(m，n)－凝聚环。

(1)⇒(7).设 FPnd(P)=m，因为 R是右(m，n)－凝聚环，所以FPn+1d(P)=m，从而有投射分解

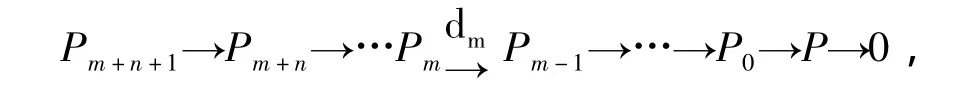
其中 Pm，…，Pm+n+1是有限生成的。设 Ki=kerdi，则Km+n－1是有限表现的。由于对于任意左R－模集{Mi}i∈Ⅰ，有如下的行正合交换图，

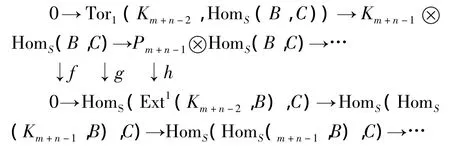
由［9，引理3.60］可知，任意有限表现模P和内射模C有

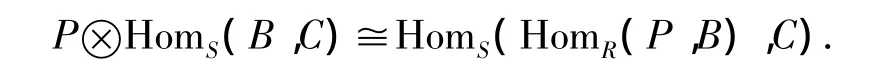
因为 Km+n－1，Pm+n－1是有限表现的，所以 g，h 同构，从而f也是同构的。因此，

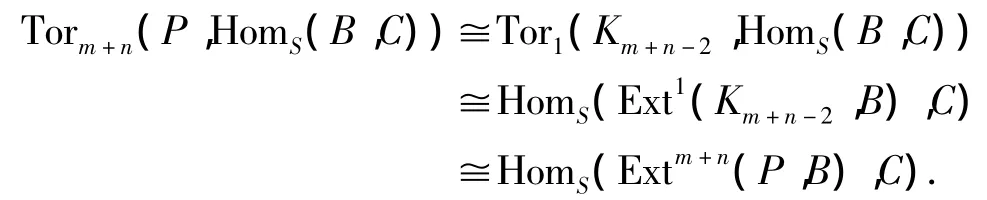
(7)⇒(8).设 S=Z，C=Q/Z，B=M，则由(7)可知有(P，M*)≅(P，M)*，因此(8)成立。

(8)⇒(9).注意到0→M*→M＊＊是可裂的(由［1，命题20.14］)。若 M＊＊是(m，n)－内射的，由(8)可知M＊＊＊是(m，n)－平坦的，因此 M*是(m，n)－平坦的，又由(8)可知M是(m，n)－内射的.反之，若M是(m，n)－内射的，由(8)可知M*是(m，n)－平坦的，从而由命题2.3可知M＊＊是(m，n)－内射的。

(9)⇒(10).U＊＊是(m，n)－平坦的，则由命题2.3可知，当且仅当 U＊＊＊是(m，n)－内射的，由(9)可知，当且仅当U*是(m，n)－内射的，从而又由命题2.3可知，当且仅当U是(m，n)－平坦的。

(10)⇒(4).由命题2.2 可知，⊕ⅠR 是(m，n)－平坦的，所以由(10)可知(⊕ⅠR)＊＊≅(ⅡⅠR*)*是(m，n)－平坦的.又由［10，引理1(1)］可知，⊕ⅠR*是ⅡⅠR*的纯子模，从而(ⅡⅠR*)*→(⊕ⅠR*)*→0可裂，因此ⅡⅠR＊＊≅(⊕ⅠR*)*是(m，n)－平坦的。又由［10，引理 1(2)］可知，ⅡⅠR 是ⅡⅠR＊＊的纯子模，从而由命题2.4可知.ⅡⅠR是(m，n)－平坦的。

［1］Anderson F W，Fuller K R.Ring and categories of modules:2nd edition［M］.New York:Spring － Verlag，1992.

［2］佟文廷.同调代数引论［M］.北京:高等教育出版社，1998.

［3］Ng H K.Finitely presented dimension of commutative rings and modules［J］.Pacific of Math，1984，113:417 －431.

［4］丁南庆.模的有限生成维数［J］.南京大学学报数学半年刊，1989(1):107－111.

［5］龚志伟，翟峰，周德旭.关于n－表现维数［J］.福建师范大学学报，2009，25(2):6 －9.

［6］Chen J L，Ding N Q.On n － coherent rings［J］.Comm.Algebra，1996，24:3211 －3216.

［7］Goodearl K R.Ring theory［M］.New York:Marcel Dekker，1976.

［8］Glaz S.Commutative coherent rings［M］.Lect.Notes Math.1371，Berlin:Springer－ Verlag，1989.

［9］Rotman J J.An introduction to homological algebra［M］.New York:Academic Press，1979.

［10］Cheatham T J，Stone D R.Flat and projective character module［J］.Proc.Amer.Math.Soc，1981，81:175 －177.