函数在区间上可微的一个充分条件
冯韩梅,赵华新
(延安大学 数学与计算机科学学院,陕西 延安 716000)
众所周知,当函数在区间上左可微时,并不一定在区间上可微。本文将讨论函数在左可微的条件下函数的可微性。即当函数在左开右闭的区间上实值连续且左可微,左导数连续时,得到函数在该区间上连续可微。
定理1 设w是(a,b]上实值连续且左可微的函数。记D-w(t)为w的左导数。如果w(b)=0且D-w(t)≤0,对于 t∈(a,b],则 w(t)≥0,对于 t∈(a,b]。
证明 首先考虑D-w(t)<0。若结论不成立,则∃t1∈(a,b),使得 w(t1)<0。
令t0=sup{t:w(t)<0},则w(t0)=0。由上确界的定义,∃{tn},使得tn→t0-,w(tn)<0。因此,
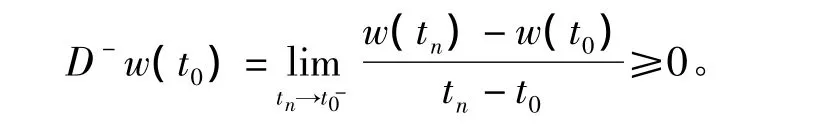
这与D-w(t)<0矛盾。所以在(a,b]上有w(t)≥0。
考虑一般情形D-w(t)≤0。
对∀ε>0,令Wε=w(t)+ε(b-t),则 Wε(b)=0。

由前段证得的结论,有Wε(b)≥0。即w(t)≥-ε(b-t),由 ε 的任意性,有 w(t)≥0,t∈(a,b]。
注 设w是(a,b]上实值连续且左可微的函数。记D-w(t)为w的左导数。如果w(b)=0且D-w(t)≥0,对于 t∈(a,b],则 w(t)≤0,对于 t∈(a,b]。
定理2 设φ是(a,b]上连续左可微的函数。若D-φ 在(a,b]上连续,则 φ 在(a,b]上是连续可微的。
证明 令g=D-φ,f(t)=φ(b)-∫btg(τ)dτ,则f(t)在(a,b]上连续,且 f'(t)=g(t)。
设 w(t)=f(t)-φ(t),则w(b)=0。且

由定理1得,在(a,b]上有 w(t)≥0。同理 -w(t)≥0,则 w(t)≤0。所以在(a,b]上 w(t)=0。
因此 φ(t)=f(t)=φ(b)- ∫btg(τ)dτ,则 φ 在(a,b]上是连续可微的。
[1]Marsden J E,Sirovich L,John F.Semigroups of linear operators and applications to partial differential equations[M].New York:Springer- Verlag,1983.
[2]王梅英.函数单调性的一个判别法[J].南京审计学院学报,2005,2(1):74 -75.
[3]胡承望.函数单调性的判定方法研究[J].长江大学学报(自然科学版),2009,6(2):154 -155.
[4]王金金,任春丽.函数的右导数与导函数的右极限的关系[J].高等数学研究,2009,5(12):41 -42.
[5]王梅英.函数严格单调的一个充要条件[J].南京审计学院学报,2009,6(3):85 -87.
[6]高民犀.具有上(下)导数的上(下)半连续函数单调性的一个充要条件[J].贵州师范大学学报(自然科学版),2004,22(3):90 -91.

