关于Smarandache伪5倍数数列的两个渐进公式

王相元，郭靖杰

(延安大学 数学与计算机科学学院，陕西 延安 716000)

1 引言和结论

对任意一个正整数，如果将其各位数字进行置换(包括恒等置换)后所得数字是5的倍数，那么这个数就为伪5 倍数，例如:0，5，15，51，52，102，…就是伪5倍数，令表示所有伪5倍数的集合。如果一个数本身不是5的倍数，但经过若干次置换后成为5的倍数，这样的数称为第二类伪5倍数，令Y表示第二类伪5倍数.在参考文献中，Smarandache教授建议我们研究伪5倍数序列的性质。关于这一问题，文献［2］证明了

这里f(n)是任意的算术函数，且M=max{|f(n)|}。

文献［3］证明了对任意的x≥1，有渐进公式

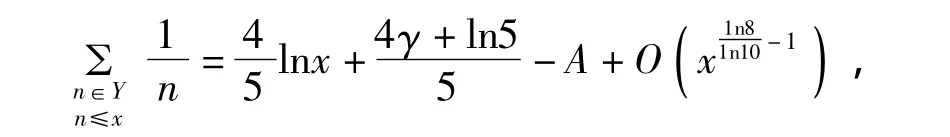
其中γ表示Euler常数，A是一个常数。本文利用解析方法研究了在集合X和集合Y上的均值，并得到了两个渐进公式，即证明了如下

定理1 对任意实数x≥1，有渐进公式

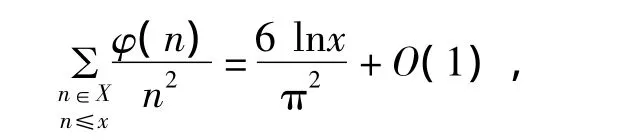
作为一项学科竞赛，他的实施主要依托于学校和学生这两个主体，其具备以下特点：一是学生的准备、训练场地主要在学校内部，与外部环境(例如企业)没有关系，这样学校和学生掌握主动权，可以投入较大的人力。物力和精力。二是该竞赛以学生为主，学生的选拔首要就是学生根据兴趣自己报名参加，这就保证了参与者的积极性，在工作中能够充分发挥主观能动性，达到事半功倍的效果。三是指导人员全部是所在高校教师，这样就排除了外部人员因素的干扰，而且指导学生参加竞赛对教师的业务能力提高、职称评定等方面也有一定的益处，因此，老师也能够全身心投入到该项工作中去。

引理2 对任意实数x≥1，有渐进公式

当地冬储还未开始，一是因为当地小麦播种季节推迟；二是因为按照惯例，当地冬储开展比较晚；三是因为当前的市场已经饱和，基层市场低迷；四是当前赊销严重，目前回款份额不大，没有足够的资金进行冬储。韩海霞表示，因为当地花生用肥要等到明年3月份，而且小麦追肥的量也不大，所以经销商现在不着急冬储。即使价格稳定下来，甚至有所下滑，仍旧不计划冬储。

由Abel恒等式可得

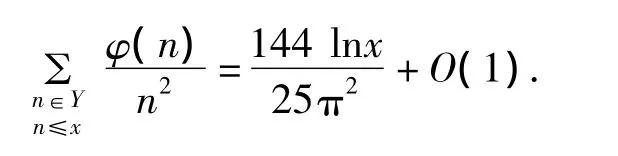
2 几个引理

这就证明了引理2。

口服升白细胞药物依从性差已成为阻碍肿瘤病人升白细胞治疗效果的重要因素，为更好地保证治疗效果，护士应根据病人及其家属认知水平、理解能力，进行个体化用药指导，还应加强健康教育、简化用药方案、建立家庭社会支持系统等。但针对出院病人如何进行更有效的健康指导，开展延续性护理服务，提高病人生活质量，还需要护理人员进一步研究。

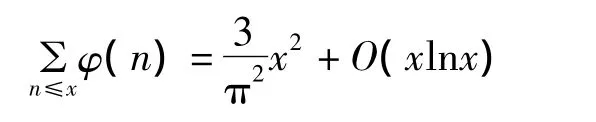
认知语言学以身体经验为出发点，参照人的认知过程，对众多语言现象尤其是隐喻进行深刻的反思和再认识，针对语言与客观世界、语言的任意性和理据性、范畴与概念、语言的多义现象等传统的语言问题提出了新见解。

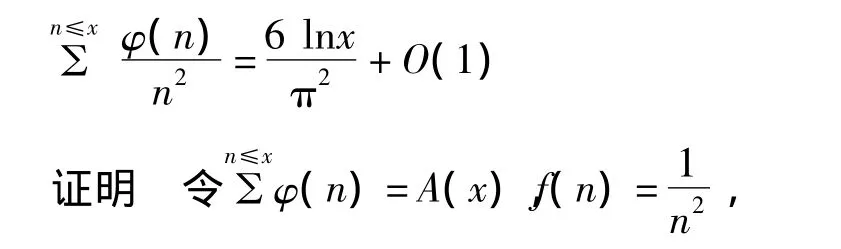
定理2 对任意实数，有渐进公式

其中φ(n)为欧拉函数。

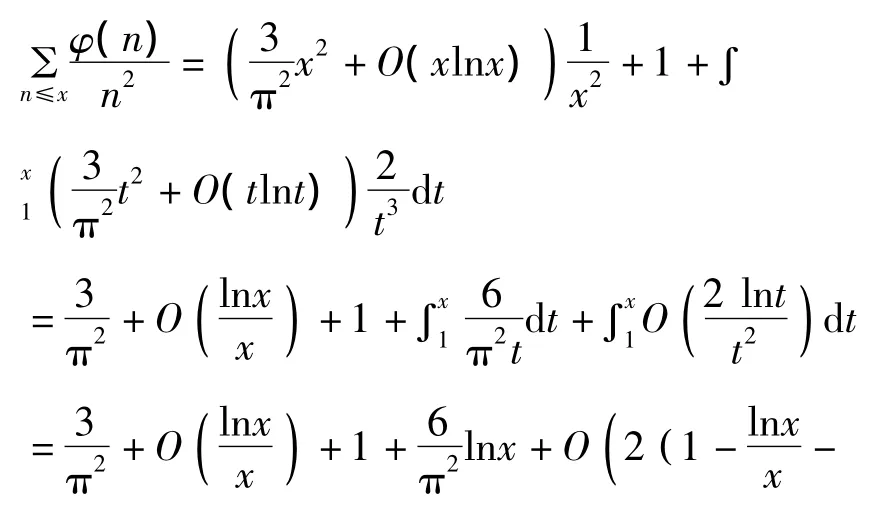
引理1［4］对任意实数x≥1，我们有

引理3 对任意实数x≥1，令表Z示所有十进制数字中各位数字为1，2，3，4，6，7，8，9 的自然数的集合，那么有渐进公式

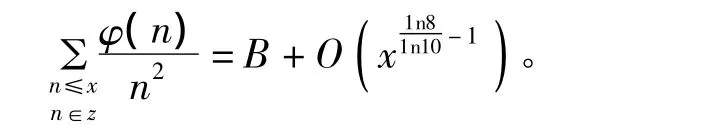
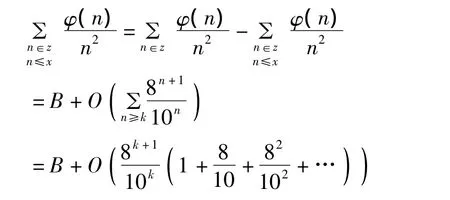
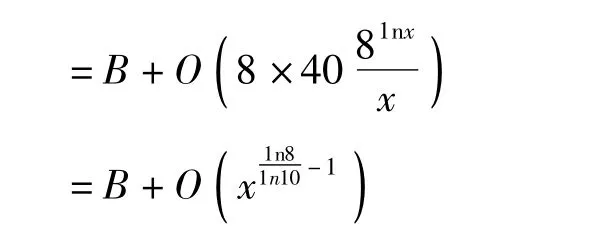
这就证明了引理3。

3 定理的证明

现在来完成定理1的证明，

三是丰富社区文化活动。加强基层文化建设，在集中居住区内规划建设乡村文史馆、文化站、文化广场等基础设施，鼓励送戏下乡、科普教育等文化服务向新型农村社区倾斜，将社区建设成为农民群众的精神家园、人文家园、和谐家园。同时深入挖掘深厚的乡土文化、创业文化，建设乡贤馆、文化广场、农家书屋等一系列文化设施，使原本的“破烂村”转变为乡土的、健康的、文化的、历史的美丽乡村。□

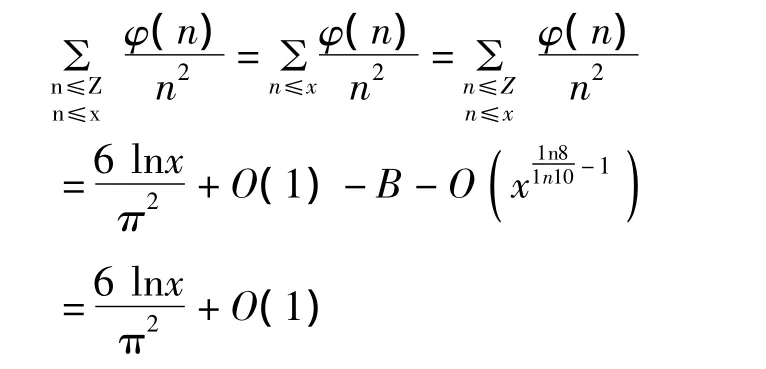
这就证明了定理1，利用同样的方法便可以证明定理2。

［1］Smarandache F.Only problem not solutions［M］.Chicago:Xiquan Publ House，1993.

［2］ZHAGN Wenpeng.Research on smarandache problems in number theory［C］.Phoenix，USA:Hexis，2004:17 －19.

［3］李洁.关于第二类Smarandache伪5倍数数列［J］.西北大学学报，2006，36(4):517 －518.

［4］Tom M Apostol.解析数论导引［M］.西南师范大学出版社，1992.