两弱伴随矩阵的关系
张 慧,岳育英,白勇菊
(1.延安大学 数学与计算机科学学院,陕西 延安 716000;2.靖边七中,陕西 靖边 718500;3.吴堡县宋家川镇教委,陕西 吴堡 728200)
定义 1[1]设矩阵 A=(aij)n×n∈Mn(C),Mij为矩阵A中元素aij的余子式,将矩阵
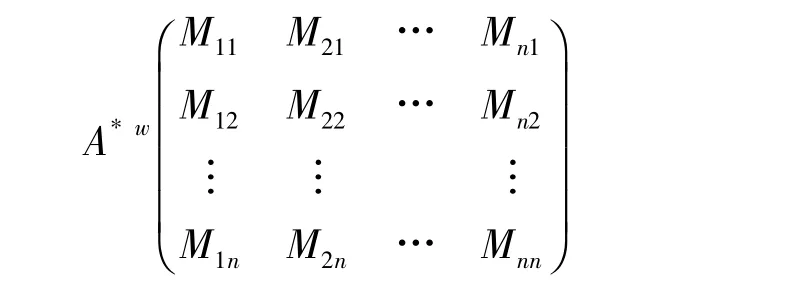
称为矩阵A的弱伴随矩阵。
定义2[2]矩阵A与B相抵(或等价)是指对矩阵A作行和列的有限次初等变换后可得到矩阵B,亦即存在初等矩阵 T1,…,Tp,S1,…,Sq使得
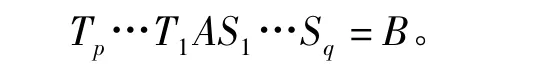
定义3[3]设矩阵A,B∈Mn(C),如果存在非奇异矩阵S∈Mn(C),使得
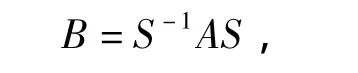
则称B与A相似。
定义4[3]设矩阵A,B∈Mn(C),如果存在酉矩阵 U∈Mn(C),使得

则称B酉等价(或酉相似)于A,如果U可以取实矩阵(因而是正交矩阵),那么就称B正交等价(正交相似)于A。
定义5[4]设矩阵A,B∈Mn(C),如果存在非奇异矩阵Q∈Mn(C),使得

则称A与B是共轭相合(或共轭合同)的;或者使得

则称A与B是转置相合(或转置合同)的。
引理 1[5]设矩阵 Eij,Ei(k),Eij(k)∈Mn(C),Eij是第一种初等矩阵,Ei(k)是第二种初等矩阵,Eij(k)是第三种初等矩阵,则

定理 设矩阵A,B∈Mn(C),
(1)若 AB=BA,则 A*wB*w=B*wA*w;
(2)若A与B相抵,则A*w与B*w相抵;
(3)若A与B相似,则A*w与B*w相似;
(4)若A与B酉等价,则A*w与B*w酉等价;
(5)若A与B正交等价,则A*w与B*w正交等价;
(6)若A与B共轭相合,则A*w与B*w共轭相合;
(7)若A与B转置相合,则A*w与B*w转置相合。
证明(1)因为AB=BA,所以
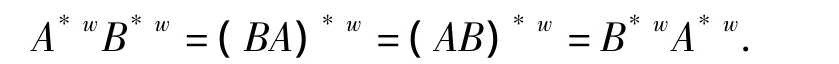
(2)因为A与B相抵,所以存在初等矩阵T1,…,Tp,S1,…,Sq使得

因为 T1,…,Tp,S1,…,Sq是初等矩阵,所以,…,…也是初等矩阵,因此A*w与B*w也相抵。
(3)因为A与B相似,所以存在非奇异矩阵T使得 T-1AT=B。
①当|A|≠0,则|B|=|T-1AT|=|A|≠0,

②当|A|=0,|B|=|T-1AT|=|A|=0,则必存在 δ>0,当0<t<δ时,

由①知存在非奇异矩阵Q使得

上式两端矩阵的元素都是关于t的n次多项式,当0<t<δ时,对应元素相等,因此对任何t,(B+tE)*w=Q-1(A+tE)*wQ 都成立,取 t=0,B*w=Q-1A*wQ。
故A*w与B*w相似。
同理可证(4),(5)也成立。
(6)因为A与B共轭相合,所以存在非奇异矩阵T,使得 THAT=B。

因为T是非奇异矩阵,所以(TH)*w也是非奇异矩阵。
故A*w与B*w共轭相合。
同理可证(7)成立。
[1]李顺琴,刘兴祥.弱伴随矩阵及其性质[J].延安大学学报,2005,24(4):24 -26.
[2]张贤科,许甫华.高等代数学[M].北京:清华大学出版社,2004.
[3]Roger A H,Charles R J.Matrix analysis[M].北京:人民邮电出版社,2005.
[4]陈景良,陈向晖.特殊矩阵[M].北京:清华大学出版社,2001.
[5]张慧,刘兴祥.弱伴随矩阵的关联性质[J].河南科学,2011,29(3):32 -35.

