AHM在应届毕业生就业选择中的应用
岳育英,刘兴祥,杨 楠
(延安大学 数学与计算机科学学院,陕西 延安 716000)
1 问题的重述
现代社会,就业难已成为普遍现象。许多企业招聘不到急需的人才,而很多学生也寻找不到适合自己的岗位,造成“就业难,用工荒”的情况。许多学生对自己目前的工作岗位深感不满,企业对应聘来的学生大失所望,给双方都带来了不小的损失,如何解决这类问题呢?
2 问题的分析
首先,这是一类无结构且缺乏必要数据的决策问题。针对这一问题,20世纪70年代就有人提出了层次分析法(AHP)[1]。但层次分析法(AHP)要对判断矩阵的一致性进行检验,需大量计算,给解决实际问题带来了诸多不便[2]。鉴于此,1997年北京大学数学科学学院程乾生教授提出一种新的简便的决策方法,即属性层次模型(AHM)[3]。文章利用属性层次模型(AHM)建立评价系统模型,得到就业选择的解决方案;其次,影响学生就业选择的因素主要有:工作环境、薪资待遇、晋升空间、团队精神等。而企业对人才选择要求则更多,如能力方面:创新能力、沟通能力、应变能力;个性方面:责任心、事业心、自信心;价值观方面:求职动机、工作态度;外表方面:身高、外貌、气质。
3 基本假设
(1)假设在2012年年初至岁末,我国经济按以往趋势平稳增长,没有发生任何金融危机、自然灾害、社会暴乱等现象。
(2)假设在2012年毕业生人数没有出现异常,给出的大学生毕业群体在就业方面的影响因素具有一定的代表性,其他影响他们就业的因素可不予考虑。
(3)假设企业选择人才的评价方式具有一定的代表性,其他影响企业评判人才的因素可忽略不计。
(4)假设参加招聘的均是专业与计算机相关的学生,招聘的单位均是需要此类人才的企业。
4 模型建立与求解
4.1 属性层次模型法的原理
设 C 为一准则,m1,m2,…,mn为 n个元素,比较两不同元素mi和mj对准则C的相对重要性[4],分别记为 mij和 mji,且满足:
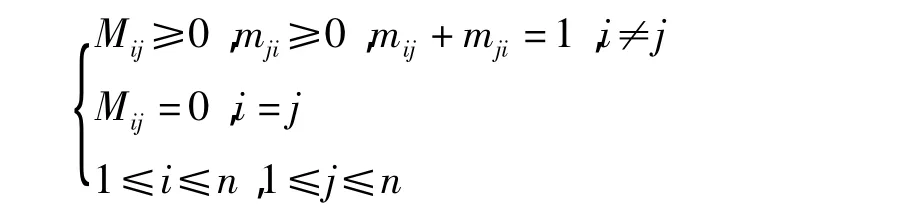
则相对属性mij组成的n阶矩阵A=(aij)称为属性判断矩阵。相对属性测度mij可由比例标度aij确定,如下式(1),其中k为大于2的正整数,β≥1(通常取1或2),本文取β=2,则式(2):
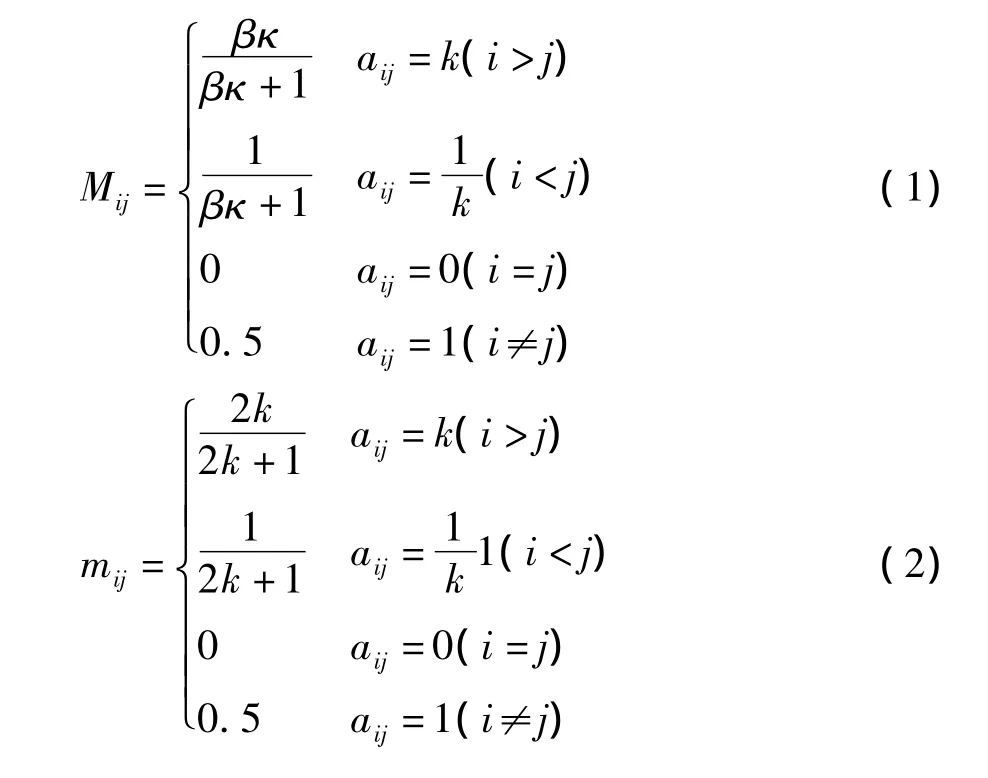

表1 比例标度
属性判断矩阵和相对权重可表示为:

其中WAi=Σmij(i=1,2,…,n)为相对权重。
4.2 属性层次模型的应用
利用属性层次模型进行决策的步骤如下:
(1)根据组成问题各个元素之间的关系,建立递阶层结构;
(2)构造属性判断矩阵并计算相对属性权重;
(3)计算方案对目标的合成权重;
(4)根据所给条件进行计算,从而做出判断或决策。
4.3 建立双方评审的评价层次模型
学生评价招聘单位的层次结构模型如图1:
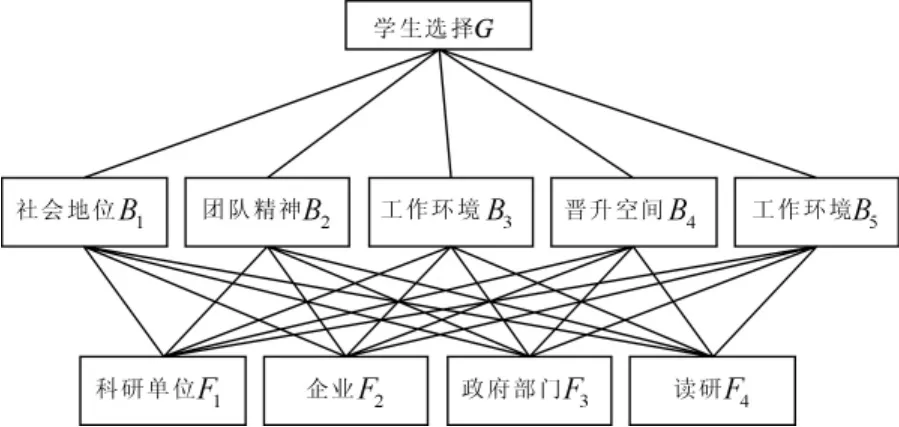
图1 层次结构模型图
构造属性判断矩阵

根据属性判断矩阵计算相对权重得到如下结果:应聘学生评价招聘单位的相对权重
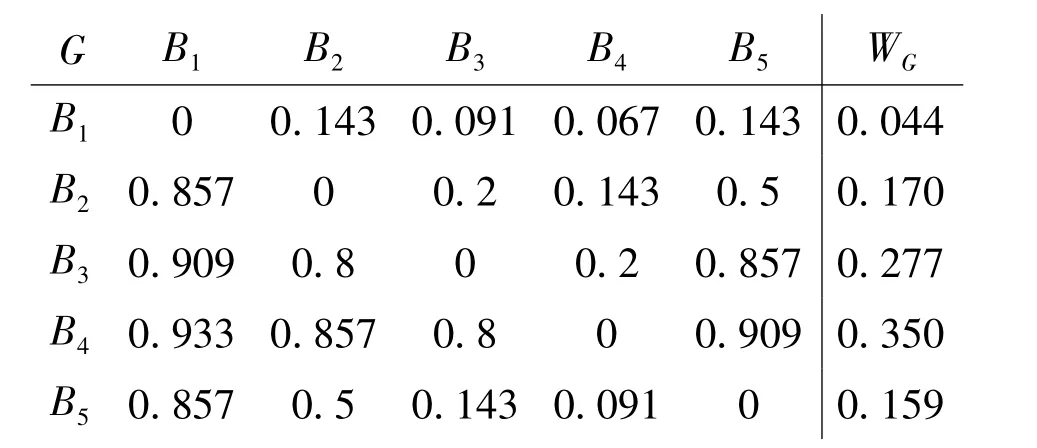
把 F1,F2,F3,F4分别按 B1,B2,B3,B4,B5的指标进行两两比较[5],即可得 B1,B2,B3,B4,B5的 AHP 判断矩阵,AHM属性判断矩阵和相对权重为WB1,WB2WB3,WB4,WB5。

AHM属性判断矩阵和相对属性权
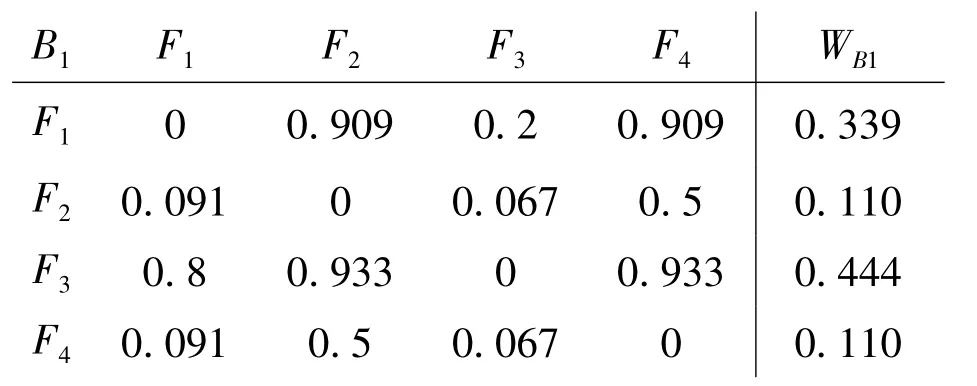

AHM属性判断矩阵和相对属性权
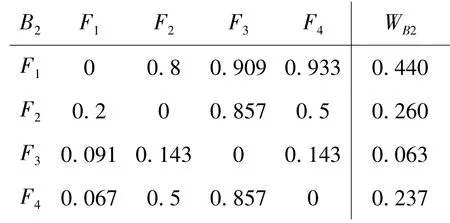

AHM属性判断矩阵和相对属性权
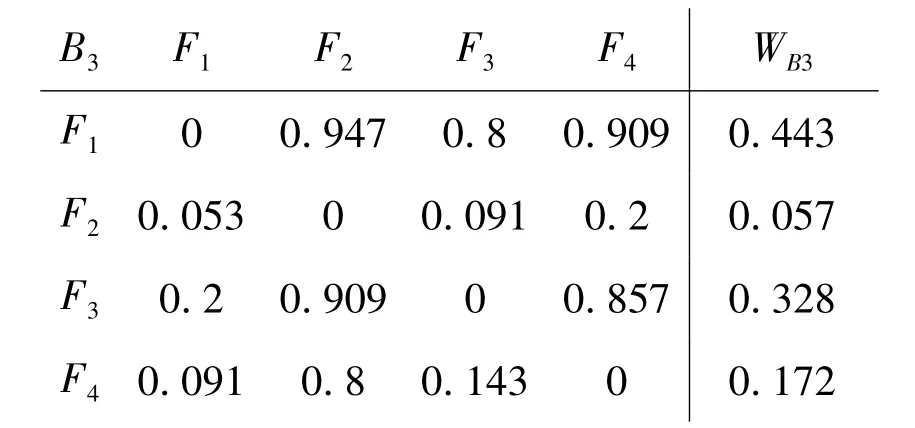
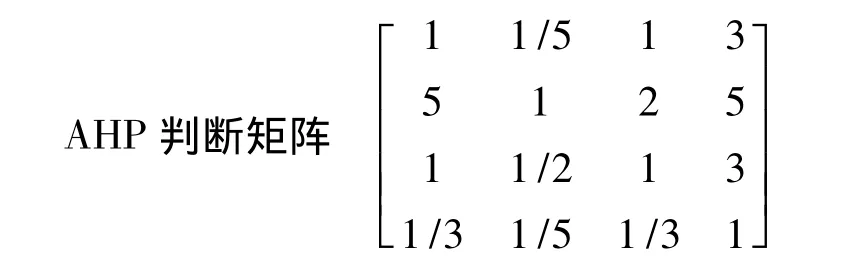
AHM属性判断矩阵和相对属性权
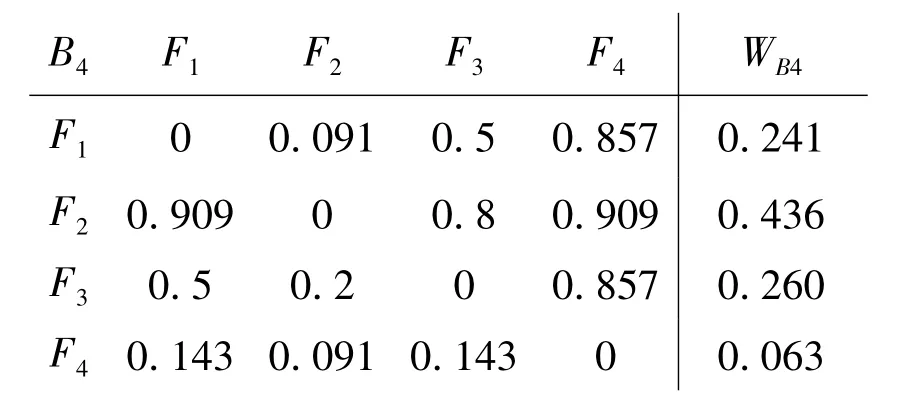

AHM属性判断矩阵和相对属性权
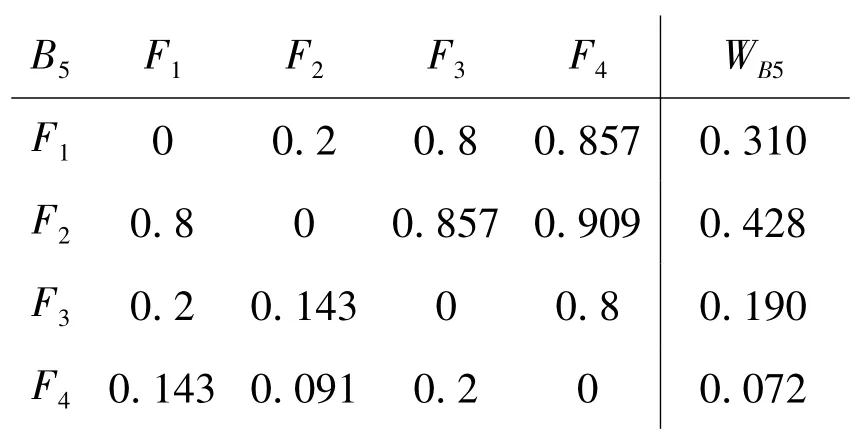
合成属性权为:WGB=(WB1,WB2,WB3,WB4,WB5)WG
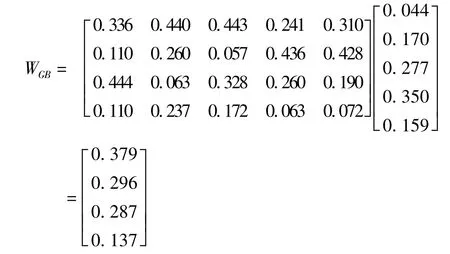
用归一法[6]将相对权重转换为评点:Si=(/max()÷ξ),i=1,2…,n,ξ=10,
相对权重转换评点为:S=(SF1,SF2SF3SF4)=(10,7.8,7.6,3.6)。
根据上述评点,企业依次排序为 F1,F2,F3,F4。
招聘单位评价应聘学生的属性层次模型如图2。
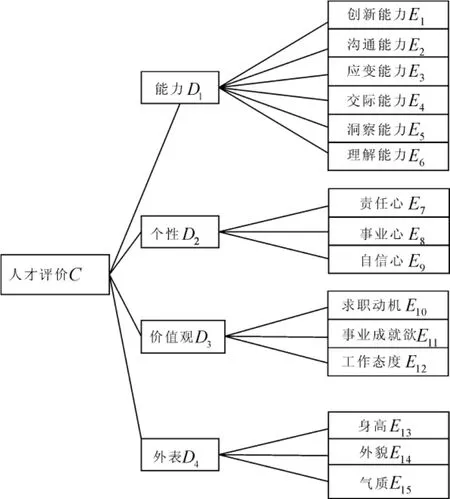
图2 属性层次模型图
1)构造各个影响因素属性判断矩阵:

根据属性判断矩阵计算得应聘学生的相对权重为:
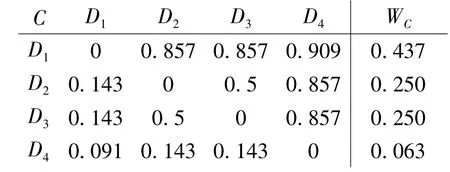
2)构造各个影响因素属性判断矩阵和相对属性权:
AHP判断矩阵

AHM属性判断矩阵和相对属性权
3)计算各个影响因素对目标C的相对属性权
设企业单位对学生的总体评价最高分为100分,则各项影响因素的评分为 13,10,4,9,6,2;15,8,2;8,15,2;2,3,1。
举例来说,现有4位应聘学生,他们的基本指标见下表

根据上述评点,学生排序依次为 P2,P3,P1,P4。
5 小结
程乾生教授指出,AHP相当于重量模型(或举重模型),AHM相当于球赛模型。在球赛模型中,甲队胜乙队,乙队胜丙队,并不要求甲队一定要胜丙队。因此,在AHM方法中,可不做一致性检验。运用上述属性模型建模方法建立模型,可以解决现实生活中对专业要求较高的行业和企业招聘。如果有n个应聘学生和m个招聘单位,利用属性层次模型尽可能避免招聘单位引进人才时的盲目性,使人才能更加符合用人单位的需求,也可以使大学生更加理性得选择较适合自己的工作,达到双赢的目的。
[1]Saaty T L.The analytic hierarchy process[M].New York:Mc-Graw – Hill International Book Company,1980.
[2]赵玮,岳德权.AHP的算法及其比较分析[J].数学的实践与认识,1995,25(1):6 -9.
[3]程乾生.属性模型AHM—一种新的无结构决策方法[J].北京大学学报,1998,34(1):10 -13.
[4]魏世存,蔡骅.多人层次分析几何平均算法原理[J].南京理工大学学报,1992(6):65-68.
[5]彭剑锋.员工素质模型设计[M].北京:中国人民大学出版社,2003.
[6]萧鸣政.人员测评与选拔[M].上海:复旦大学出版社,2005.

