一类一维齐次Moran集的维数结果

乔育,付晓慧,李彦哲

(广西大学数学与信息科学学院, 广西南宁530004)

0 引言

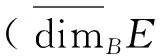
本文利用一维齐次Moran集的基本区间形成的连通分支, 定义一类特殊的比齐次完全集与{mk}-拟齐次Cantor 集更广泛的一维齐次Moran集，即{mk}-齐次Moran 集, 并得到了该类集合packing维数与上盒维数一些结果。

1 预备知识

定义1[1]一维齐次Moran集。设I为R上的非空闭区间, 集合A的直径记为|A|,A的内部记为int(A)。

称I的闭区间族Fk={Iσ:σ∈Dk}满足一维齐次Moran结构(I,{nk},{ck})。 若I∅=I，对∀σ∈Dk-1,则Iσ*1,Iσ*2,…,Iσ*nk是Iσ的闭子区间, 且int(Iσ*i)∩int(Iσ*j)=∅对∀i≠j成立; |Iσ*j|/|Iσ|=ck对任意1≤j≤nk+1成立。

关于一维齐次Moran集的更多内容见参考文献[7-11]。

不失一般性，本文假设Iσ*1,Iσ*2,…,Iσ*nk从左往右排列。

为进一步研究一维齐次Moran集的维数性质, 本文利用由基本区间形成的连通分支定义一类特殊的一维齐次Moran集，即{mk}-齐次Moran集。

定义2{mk}-齐次Moran集。设E∈M(I,{nk},{ck}), 满足对∀k≥1,σ∈Dk-1,Iσ*1,Iσ*2,…,Iσ*nk任意连接形成mk(1≤mk≤nk)个连通分支, 从左往右排列记为Jσ*1,Jσ*2,…,Jσ*mk(称它们为k阶连通分支), 称E为由I,{nk}k≥1,{ck}k≥1定义的{mk}-齐次Moran集。 用L*(I,{nk},{mk},{ck}) 表示由I,{nk}k≥1,{ck}k≥1定义的{mk}-齐次Moran集构成的集族。

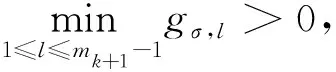
2 主要结果

设∀k≥1,σ∈Dk-1,记

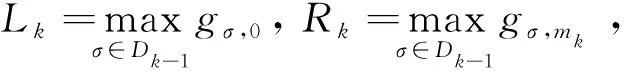
定理1设E∈L*(I,{nk},{mk},{ck}), 如果supk{mk}<∞, 则

(1)

注1{mk}-拟齐次Cantor集[6]一定为{mk}-齐次Moran集, 因此定理1推广了文献[6]中定理2.3的结果。

(2)

由定理2可立得下面的推论。

推论1设E是定理2中的{mk}-齐次Moran集, 若Lk=Rk=0对∀k≥1成立, 则

(3)

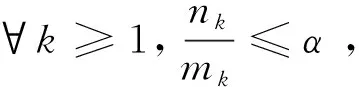
3 定理1和定理2的证明

下面2个引理是证明定理1和定理2的关键。

引理1[1]设E∈M(I,{nk},{ck})为一维齐次Moran集, 则

引理2[12]设E∈L*(I,{nk},{mk},{ck}), 则

3.1 定理1的证明

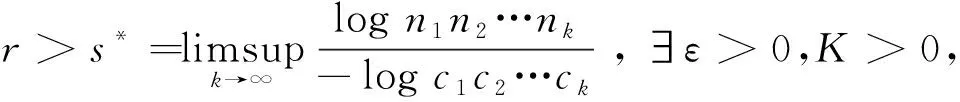
(4)

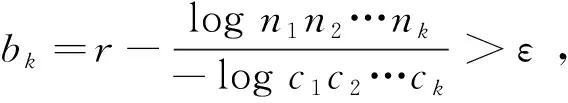
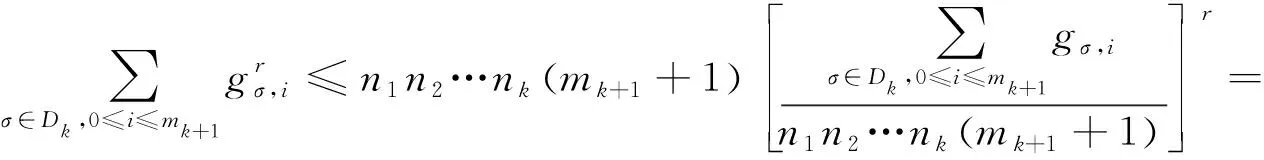
(5)

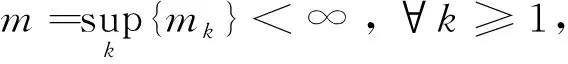
3.2 定理2的证明

先估计公式(2)右边不等式。

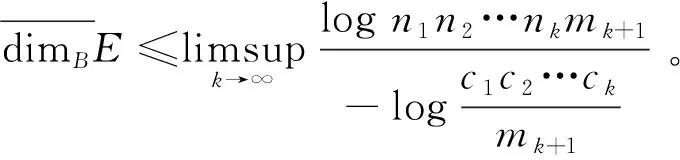
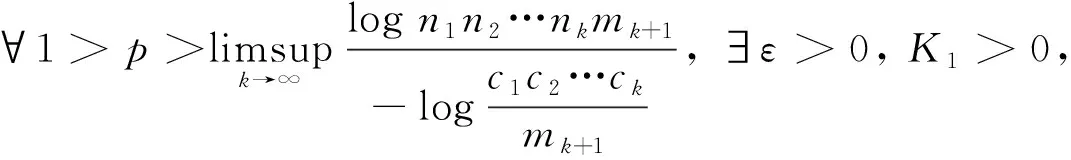
即

(6)

注意到δk≤2-k,mk+1≤2mk, 结合公式(5)、(6)有

下面估计公式(2)左边不等式。

命题2 设E∈L*(I,{nk},{mk},{ck})满足定理2条件,则

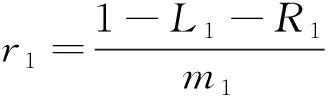
故

从而有

(7)

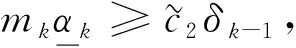
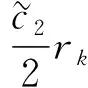
(8)

(9)

故

类比条件②下的分析, 可得

(10)

当k→∞时, 有rk→0, 利用公式(7)至公式(10)，有

综合命题1和命题2可推出定理2成立。

4 结论

本文证明{mk}-齐次Moran集的packing维数和上盒维数在supk{mk}<∞时可达到所有一维齐次Moran集对应维数的最小值，推广文献[6]的结论,并给出该类集合的上盒维数在一些条件下的取值范围,同时找到其达到准确值的一个充分条件，在一定条件下推广文献[4]的结论。