基于频率法的悬索桥锚跨索股索力精细化计算分析

齐东春，宋敬，刘章军，胡海龙

(1.三峡大学土木与建筑学院, 湖北宜昌443002；2.湖北省防灾减灾重点实验室， 湖北宜昌443002；3.武汉工程大学土木工程与建筑学院, 湖北武汉430074)

0 引言

锚跨是悬索桥结构受力的关键部位，锚跨索股索力的控制影响着悬索桥锚固体系的安全。在施工过程中，锚跨索股索力控制如果出现较大的偏差，会造成边跨和锚跨索力的不平衡，从而引起散索鞍的转动或滑动，同时索股也可能在鞍槽内出现滑动，进而引起边跨线形的改变。锚跨索股的控制精度影响着悬索桥结构的线形和安全，因此需要对每根索股索力进行准确测量及张拉控制。

目前锚跨索力现场测试的主要方法包括油压表法、压力传感器法和频率法[1-2]。油压表法虽然可以直接读出索力，但是在分批次的锚跨索股索力调整过程中，后面批次的索股索力的调整会对前一批次索股的索力造成影响，造成油压表所测得索力数据失效,因此，只有最后一根调整完成的索股的索力用油压表直接读出是有效的。压力传感器法测试精度高;但是其成本较高并且在施工过程中及施工完成后无法拆除，因此很难对全部的索股进行布置并测试。频率法因简单、快捷、经济和实用成为普遍采用的一种测试方法。通常先采用振动法测试出索股的自振频率，再利用索力与频率之间的关系式，求得索力[3-6]。

大量学者对悬索桥锚跨索股的索力测试进行了分析研究，许汉铮等[7]提出锚跨索股拉杆与联接板处、索股与拉杆结合处、索股与散索鞍处为铰接的锚跨索股的力学模型。甘泉等[8]用固支欧拉梁的振型函数近似两端固结拉索的振型函数，采用能量法推导出拉索索力的计算公式。公式简单实用，方便现场快速测试索力，上述文献均将锚跨索股当作匀质材料的索股，未按实际情况考虑拉杆的影响。范剑锋等[9]考虑拉杆的抗弯刚度，通过Hamilton变分原理推导出悬索桥锚跨拉杆与索股组成的索梁组合结构的索力修正算法。该方法考虑了拉杆的抗弯刚度影响,但忽略了索股抗弯刚度影响。艾玉麒等[10]考虑叉耳对吊杆振动的影响，近似处理吊杆与叉耳部分的振型函数为同一振型函数，采用能量法推导出吊杆索力与自振频率之间的显式表达式;但该方法用于悬索桥锚跨索力计算时，由于悬索桥锚跨拉杆占总长度比例较大，因此拉杆和索股不能近似处理为同一振型函数。文献[11-12]基于解析法建立锚跨索股的力学模型，利用能量法进行求解，得出索股索力与自振基频的关系表达式，但是并没有考虑拉杆和索股弯曲刚度的影响。

根据锚跨索股实际构造特点建立解析法力学模型，索股和拉杆分别采用不同的欧拉梁的振型函数，考虑索股、拉杆抗弯刚度及锚头质量的影响，采用能量法推导出索力与频率的显式表达式。

1 锚跨索股计算模型

锚跨索股从散索鞍散开后，其末端为一个起连接作用的锚头，并通过螺母与拉杆的前端相连。拉杆的另一端穿过联接板，通过螺母与联接板相连，拉杆在联接板内存在一定的间隙，可以简化为铰接。锚跨索股构造如图1所示。

1.索股；2.拉杆；3.锁紧螺母；4.六角螺母；5.锚头；6.拉杆；7.保护罩；8.联接板；9.联接筒；10.球面螺母；11.锁紧螺母；12.前锚面 图1 锚跨索股构造 Fig.1 Structure diagram of anchor span cable strand

将锚跨结构进行简化等效，简化模型如图2所示。拉杆的长度为l1，抗弯惯性矩为I1，弹性模量为E1，每延米质量为m1。索股的长度l2，抗弯惯性矩为I2，弹性模量为E2，每延米的质量为m2，锚跨部分总长度为l=l1+l2。索股锚头质量为m3，简化为一个集中质量。

由于锚跨索股较短并且拉杆占总长度比例较大，因此需要考虑拉杆长度和锚头质量等因素对索力测试的影响。锚跨索股分析模型的基本假设如下:

①索的垂度忽略不计；

②索在微小振动时，索力变化忽略不计；

③索仅发生竖向平面内的振动，忽略轴向位移的影响；

④拉杆下端、索股上端、拉杆与索股连接处均简化为铰接。

1.1 振动方程建立

根据上述假定，忽略垂度的影响，采用结构动力学基本原理分别对锚跨索股结构部分的拉杆和索股建立自由振动的微分方程[13]，

(1)

式中：y1和y2为拉杆和索股的竖向平面内位移函数；T为拉索的索力。

由于上述2个方程结构形式相同，因此选取第一个方程式进行分析

(2)

假设方程的解为

y1(x,t)=φ1(x)·q1(t)，

(3)

式中：φ1(x)为振型函数；q1(t)为广义坐标。该方程的通解为

q1(t)=asin(υt+θ)，

(4)

φ1(x)=Ccosh (αx)+Dsinh (αx)+Hcos (βx)+Fsin (βx)，

(5)

其中：

式中：υ为结构的自振圆频率；θ为相位角；C、D、H、F为振型系数。

利用能量法推导索力和频率的显式表达式，需要求解出振型函数，但是上述方法对振型系数的求解过于复杂。因此，对拉杆和索股的振型函数采用忽略轴力的欧拉梁的振型函数进行代替，上述振型函数可简化为

φ1(x)=C1cosh (α1x)+D1sinh (α1x)+H1cos (α1x)+F1sin (α1x)，

(6)

φ2(x)=C2cosh (α2x)+D2sinh (α2x)+H2cos (α2x)+F2sin (α2x)，

(7)

其中：

1.2 边界条件

通过分析得到了拉杆和索股的振型函数方程，两组方程含有C1、C2、D1、D2、H1、H2、F1、F2及υ1共9个未知系数,需要根据模型的边界条件进行求解[14]。

①根据上述假定，拉杆下端为铰接，则位移为0，弯矩为0，可得

其中：

C1+H1=0，

②索股上端在散索鞍切点处为铰接，则位移为0，弯矩为0，可得

其中：

C2cosh (α2l)+D2sinh (α2l)+H2cos (α2l)+F2sin (α2l)=0，

③索股与拉杆连接处为铰接，索股和拉杆在此处拥有共同的平动位移，且剪力平衡，弯矩为0，可得

φ1(l1)=φ2(l1)，

E2I2φ‴2(l1)-E1I1φ‴1(l1)=0，

其中：

根据上述分析可以得到如下矩阵方程：

AB=0，

(8)

矩阵A的各元素如下：

其中：

因为振型函数不能为0，因此振型系数矩阵B的每一项元素不全为0，则det|A|=0。又因为振型系数矩阵B的各元素之间具有一定的比例关系，并令C1=1，则可以得到振型系数矩阵B中的各元素表达式。

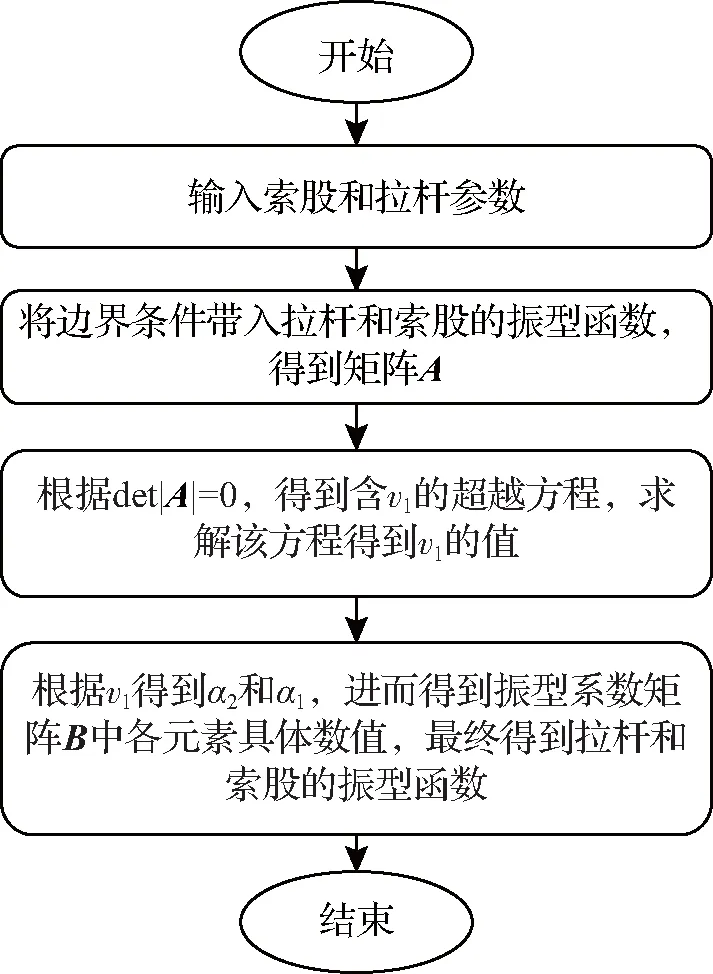
图3 振型系数计算流程Fig.3 Flow chart of vibration mode coefficient calculation

其中：

C1=1，D1=-1，
H1=e-2α2l1·sin (α1l)/sin (α2l2)，
F1=-e-2α2l1·cos (α1l)/sin (α2l2)，
C2=0，D2=e-2α2l1/sinh (α1l1)，
H2=0，F2=e-2α2l1/sin (α1l1)。

由det|A|=0，可以得到关于υ1的超越方程，即

F(υ1)=0。

(9)

该方程为含有一个未知数υ1的超越函数，求解该超越函数，可以得到υ1的值，进而得到振型系数矩阵B各元素的具体数值。最终确定拉杆和索股的振型函数，求解过程如图3所示。

1.3 能量法

锚跨索股结构振动的动能[15]为

(10)

将式(6)、(7)代入式(10)中，则锚跨索股结构最大动能为

锚跨索股结构振动的势能为

(11)

将式(6)、(7)代入式(11)中，锚跨索股结构最大势能为

根据能量守恒定律，最大势能等于最大动能，即Vmax=Wmax，可以得到

(12)

经转化可以得到

(13)

其中：

2 算例验证

某主跨1 160 m的钢箱梁悬索桥，主缆采用预制平行钢丝索股法(PPWS)进行架设。每根主缆由85股127丝和6股91丝索股组成，单丝为直径6 mm的镀锌高强钢丝。主缆锚固采用预应力锚固系统，主缆索股在散索鞍散开后，通过拉杆、锚固连接器连接到预应力钢绞线上，通过预应力将索股拉力传递到锚体混凝土上。锚跨结构示意图如图4所示。

图4 锚跨结构示意图Fig.4 Anchor span structure schematic diagram

选取其中几根索股进行测试，其中锚头的质量m3=394 kg。索股锚跨连接结构各部分参数见表1。

表1 锚跨索股结构各部分参数Tab.1 Parameters of each part of anchor span cable strand structure

选取62号索股进行分析，由式(8)计算可以得到α2l2=3.193，α1l1=0.276。代入式(13)可以得到如下索力计算公式，其中f为锚跨索股的自振基频。

(14)

2.1 有限元模型

采用ANSYS建立考虑散索鞍影响的锚跨索股精细化有限元模型。为尽量减少简化，拉杆按双拉杆考虑，并按拉杆实际截面考虑其抗弯刚度。索股按钢丝集束体考虑其抗弯刚度，索股的抗弯刚度介于按钢丝集束体完全分散和完全粘接2种情况计算所得的刚度。拉杆及索股均采用BEAM4单元模拟，并通过初应变来输入拉杆及索股中存在的索力。索股与拉杆间通过锚头相连，锚头按其等效面积采用BEAM4单元模拟，通过调整质量密度保证锚头质量的准确性。拉杆下端采用铰接，拉杆上端与锚头间通过节点自由度的耦合与释放实现固结与铰接的转换，索股下端与锚头间则采用固结。

为了准确考虑散索鞍对索股的约束关系，沿鞍座圆弧划分若干节点以模拟鞍座圆曲线，并将索股与鞍座可能相切的位置细分，各节点与鞍座圆心用刚度较大的单向只受压杆LINK10单元相连。鞍座圆弧上相邻两节点则采用BEAM4单元连接，以模拟与鞍座相接触部分的索股[17]。鞍座最上端点及鞍座圆心均采用固结。在计算索股与鞍座切点位置时，索股下端点到鞍座最上端点间索股的总无应力长度保持不变，与成桥时索股无应力长度相等，关于成桥状态锚跨索股无应力长度的计算可参考文献[17]。在有限元求解时，根据悬空段索股与接触段索股总的无应力长度保持不变这一条件，当模拟鞍座的某些只受压杆单元出现拉力时便退出工作，相当于索股与鞍座脱离，这样便模拟了索股与鞍座切点位置的变化。

图5 有限元模型AFig.5 Finite element model A

由于索股处于张紧状态，因此应采用大变形有应力模态法计算结构的频率，以考虑结构的几何刚度的影响。首先对结构施加自重进行静力计算，并打开几何非线性开关及应力刚化效应，以获得结构在自重及指定索力下的结构状态，并得到索股与鞍座的切点坐标。在此基础上修正节点坐标以得到正确的应力，同时将位移清零。然后定义模态分析参数及选项进行特征值求解，计算出指定索力对应的频率和振型。为了进行对比分析，把考虑散索鞍影响的模型称为有限元模型A，把不考虑散索鞍影响的模型(即索股与散索鞍处采用铰接)称为限元模型B。有限元模型各参数的取值见表1，有限元模型A如图5所示。

2.2 对比分析

锚跨索股索力通过布置在拉杆上的压力传感器进行测试，频率的测试采用索力动测仪进行测试。选取上述每根索股的实测数据进行对比，实测频率和对应压力环实测索力关系如图6所示。

图6 索力-频率对应图Fig.6 Cable force-frequency correspondence graph

为了验证本文计算模型和方法的正确性，通过本文推导的公式(14)、有限元模型计算差异及文献[16]中公式计算所得索力同压力传感器实测索力进行对比，计算结果对比分析见表2。

表2 计算结果对比分析Tab.2 Comparative analysis of calculation results

根据表2可知，采用文献[16]中公式进行计算时，计算结果比本文公式计算结果误差偏大，文献[16]中公式仅考虑了索股抗弯刚度的影响，并不能考虑拉杆部分的影响。本文公式(14)计算结果与压力传感器实测结果及有限元模型A计算结果吻合，且误差的变化规律相一致。公式计算的结果与实测索力的结果误差不超过2%。说明本所文采用的模型及计算方法接近实际情况，计算结果较为接近实测索力，精度满足一定的要求。

通过对有限元模型A和有限元模型B进行对比发现，有限元模型A计算精度较有限元模型B得到提高，原因是有限元模型A模拟了索股切点在散索鞍鞍座圆弧处位置的变化，更加符合实际情况，因此有限元模型A的计算精度更高。

2.3 索股抗弯刚度及锚头质量的影响

为了研究索股抗弯刚度对索股索力测试的影响，选取51号索股进行分析，索股抗弯刚度分别取最大值(即与钢丝面积等效的圆钢棒的抗弯刚度)、最小值(即所有钢丝抗弯刚度之和)及中间值，分别为199.79、1.57、100.78 kN·m2。

通过本文公式(14)进行计算分析，在相同频率下，不同抗弯刚度下索力计算值见表3。

表3 不同抗弯刚度下索力计算值Tab.3 Calculated cable force under different bending stiffness

由表3可知，在同一频率下，索力随着抗弯刚度的增加而减小，基本呈线性变化。频率取9.284 Hz，对比3组不同抗弯刚度下的索力变化可知，公式(14)计算索力随着抗弯刚度的增加递减幅度为0.35%。抗弯刚度对索力的影响随着索股索力的增大而逐渐减少。

为了研究锚头质量对索股测试的影响，选取51号索股进行分析，采用公式(14)进行计算，锚头质量对索力计算影响见表4。计算结果表明：不考虑锚头质量时索力计算的结果较考虑锚头质量时索力计算结果相对减少约为2.3%，说明锚头对实测索力有一定影响，计算应加以考虑。

表4 锚头质量对索力计算影响Tab.4 Influence of anchor head quality on cable force calculation

3 结语

①本文提出的公式适用于悬索桥锚跨索股采用预应力锚固的情况，公式的解析模型与锚跨索股实际构造相符，并能详细考虑拉杆及索股抗弯刚度、锚头质量的影响。

②与有限元模型计算结果、压力环实测索力对比，本文提出的公式计算精度高，误差在2%以内，且变化规律一致。

③文中部分索股的计算结果表明：索股抗弯刚度对实测频率的影响不大，抗弯刚度取最大值与最小值时索股索力的差异约为0.7%，但在索股索力较小时抗弯刚度的影响会增大。索股锚头质量对实测索力影响较大，约为2.3%，计算中应加以考虑。

④索股为钢丝集束体，其抗弯刚度的确定较为困难，在应用本文公式时应先对索股抗弯刚度进行识别，特别是空缆状态时索股索力的测试应考虑索股抗弯刚度的影响。

⑤本文在公式推导时将索股上端假定为铰接，而实际上索股与散索鞍存在接触非线性，有限元计算结果显示边界条件对索股索力有一定影响，因此边界条件的影响有待进一步研究。