受压T肋加劲板腹板局部稳定试验与计算方法

陈鹏，林楚，赵秋*，肖贞科

(1.福州大学土木工程学院， 福建福州350108；2.福州市城乡建总集团有限公司， 福建福州350108；3.福建省国筑建设工程有限公司，福建福州350800)

0 引言

T形肋加劲板由于具有较好的抗弯性能、刚度较大和焊接简单等优点，经常应用于钢箱梁桥的受压翼缘、钢箱拱桥的钢拱、斜拉桥的钢塔等典型受压构件中。在较大的轴向压力作用下，其受压稳定问题比较突出[1-3]。T形肋加劲板一般由3块子板件组成，局部稳定涉及到被加劲板、T肋腹板和翼缘各子板件的局部失稳，相对于板肋加劲板更加复杂。

目前，对于T形肋加劲板的受压稳定研究相对较少，多数仅采用数值模拟的方法。傅学怡等[4]通过对大宽厚比矩形钢管柱的有限元分析，发现在相同用钢量情况下，T形肋相比板肋抗弯刚度明显增大。Shin等[5]对84个大范围长细比的T肋和板肋加劲板进行数值分析，研究发现T形加劲肋在达到轴压极限荷载时腹板的应力分布相比于翼缘更加均匀。Sadamoto等[6]通过有限元模拟的方法，研究T形肋各子板件的屈曲行为，发现T形肋腹板的屈曲行为与翼缘相比有较大的差异性。T形肋腹板由于顺桥向的短边处有横隔板支承，上下方向的长边处有被加劲板及翼缘板支承，可视为与被加劲板相同的四边简支板[7-8]，赵秋等[9-11]就采用相同的简化方法，将闭口肋腹板简化为四边简支板，并通过轴压试验研究其局部失稳破坏，得到四边简支板的失稳破坏模式，并引入初始几何缺陷的影响[12]，验证有限元模型的正确性[13]，在此基础上研究开口肋四边简支板的屈曲模态，得到开口肋刚度比对屈曲模态的影响[14]。

在上述研究中，未针对T肋加劲板腹板的受压局部稳定性能展开研究。此外，在桥梁设计中同样存在柔性加劲肋的设计，此时腹板作为连接翼缘和被加劲板的板件，其稳定性能的研究同样重要，并且局部稳定的研究是其整体稳定或整体与局部相关稳定研究的基础。因此本文在T形肋加劲板局部稳定试验的基础上，研究T形肋加劲板的数值模拟方法，再利用有限元模型进一步分析其组成板件腹板的局部稳定影响因素，并提出对应计算方法，为T形加劲肋腹板的受压稳定设计提供参考。

1 T形肋加劲板局部稳定试验

1.1 试件设计与材性

T形加劲肋的设计根据《公路钢结构桥梁设计规范》(JTG D64—2015)[15]规定，限制加劲肋的宽厚比，以防止构件发生局部屈曲。式(1)、(2)分别为相应的宽厚比限值。

(1)

(2)

式中：bs0、ts0分别为T肋翼缘外伸宽度、厚度；hs和ts分别为T肋腹板高度、厚度；fy为屈服强度。

图1 试件横截面图Fig.1 Cross section of specimen

在上述规定的基础上，为研究T肋加劲板的局部失稳破坏，受压T肋加劲板局部稳定试件分为Q345和Q420这2种不同钢材强度，所设计的T肋加劲板局部稳定试件横截面如图1所示，其参数见表1。试件设计根据薄壁杆件的弹性稳定理论，满足式(3)、(4)，在试件全截面屈服前，不发生绕试件轴向的扭转屈曲，且不发生绕截面对称轴的弯扭屈曲。

(3)

(4)

式中：σy、σω、σyω分别表示试件屈服强度、扭转屈曲应力、弯扭屈曲应力；Pω、Py分别表示扭转屈曲荷载、弯曲屈曲荷载；io表示极回转半径；y0表示截面形心与剪心的距离。

选取制作加劲板试件时同批次的钢板，制作材性试验试件，设计两类钢材对应不同厚度的标准拉伸试件[16]，得到相应的抗拉强度平均值fu分别为480.80、553.25 MPa，屈服强度fy分别为382.00、444.75 MPa，弹性模量平均值为2.06×105、2.01×105MPa。

表1 T肋加劲板试件参数Tab.1 Parameter of T-rib stiffened plate specimen

1.2 试验方案

为使试件均匀受压、不发生滑移以实现T肋加劲板稳定试件的简支边界，将试件两端的板件嵌入带有凹槽的钢板内。具体方法如下：通过设计带有略大于试件截面凹槽的钢板，并在边缘位置设计有连接孔洞，采用螺栓连接的形式与承压端板连接，组成局部稳定试件的限位装置，试件边界限位装置如图2所示。

(a) 含轮廓限位板(b) 承压端板(c) 限位装置

图3 加载示意图Fig.3 Loading diagram

图3为试件加载装置。加载设备采用福州大学1 000 t压力机，进行分级加载。第一阶段采取荷载为10 t的分级加载。当荷载达到60%的限元预估荷载，采用速度为0.3 mm/s的位移加载，直至试件破坏。

1.3 破坏现象分析

局部稳定试件破坏形态如图4所示，由图可知：各试件均发生板件的局部屈曲变形。对于试件Q3-wb11、Q3-wb14、Q4-wb11，在加载过程中，被加劲板首先发生局部变形，进而导致翼缘发生屈曲，当所加荷载达到3 368.7、3 927.3、4 458.3 kN时，试件达到极限承载力，随后板件变形增大，试件破坏，见图4(b)、4(h)、4(l)。对于试件Q3-wb12、Q3-wb13、Q3-wb21、Q4-wb21，均发生由翼缘先出现的局部屈曲，进而导致试件失稳，当所加荷载达到3 181.7、3 393.3、2 874.9、3 510.9 kN时，试件达到极限承载力，随后试件发生破坏，见图4(d)、4(f)、4(j)、4(n)。

综上所述，按照破坏的模式不同分为2类。第1类为试件Q3-wb11、Q3-wb14、Q4-wb11，当荷载为峰值荷载的0.63～0.68倍时，试件开始发生变形，其原因在于第类试件的被加劲板宽厚比大于翼缘。第2类为试件Q3-wb12、Q3-wb13、Q3-wb21、Q4-wb21，当荷载为峰值荷载的0.70～0.75倍时，试件则在翼缘中部发生局部变形。对于被加劲板及翼缘先于腹板发生破坏的原因是：在加载过程中，被加劲板由于非加载边的刚度不足，形成同翼缘一样的三边简支板，而腹板作为四边简支板，轴向刚度远大于两侧子板件，故较晚发生破坏。建议在试件加载时，可以采用角钢对被加劲板两侧进行加劲，防止被加劲板提前发生屈曲，同时在试件设计时，在本试件基础上增大腹板高度，并采用被加劲板横向焊接3个T肋的截面形式。

图4 局部稳定试件破坏形态Fig.4 Failure modes of local stability specimen

图5 局部稳定试件平均应力-应变曲线Fig.5 Average stress-displacement curves of local stability specimen

1.4 试验结果与分析

试验测得的局部稳定试件平均应力-应变曲线如图5所示。腹极试件试验值见表2。

由图5可知，T肋加劲板试件在试验中表现出相同的受力行为，曲线分为前期线性段、中期塑性段、后期下降段3个主要阶段。其中，当试件处于线性阶段时，曲线斜率不变；当试件处于塑性段时，试件起初发生微小的局部变形，试件轴向刚度与曲线斜率开始减小，平均应变增长速率增大；当试件处于后期下降段时，曲线则表现出明显的非线性特征，平均应力随应变的增大而快速降低，试件加速变形直至破坏。

结合表2可知，对于相同宽厚比的试件，σu随着材料增强而增大，但其承载能力折减的程度也越大；对于相同强度的试件，σu则随着宽厚比的增大而减小，试件越早发生屈曲；对于试件Q3-wb13、Q3-wb21，σu随腹板尺寸的增大而增大，对于越早发生局部屈曲的试件，其强度有较大的提高空间。

表2 腹板试件试验值Tab.2 Tests values of web plate specimen

2 T肋加劲板受压稳定有限元模拟方法

2.1 有限元模型

采用有限元软件ANSYS对T肋加劲板局部稳定试验进行模拟，模型均采用SHELL181有限应变壳单元进行建立，并根据第一节中的拉伸试验结果，选取2类钢材的实际屈服、极限强度建立四折线本构模型。根据试验结果可知，在加载过程中，由于端部限位装置的存在，能较好约束试件的非轴向位移，因此有限元模型选择两端固结的边界条件。有限元模型分别考虑了焊接残余应力、构件的局部初始几何缺陷的影响，其中残余应力采用文献[17]中T肋加劲板的残余应力实际值。由于试件在焊接、加工过程中板件凹凸不平，结合《冷弯薄壁型钢结构技术规范》(GB 510018—2002)[18]中的规定，按板宽的1/100乘以一阶屈曲变形值计入局部初始几何缺陷。

2.2 试验破坏模式验证

根据1.4节中的试验现象，选取具有代表性的试件Q3-wb11、Q3-wb21进行验证。在极限荷载状态下，相应试件的对比如图6所示，图中变形图、应力图的数值分别表示变形、应力强度的大小。

图6 试件破坏模式对比Fig.6 Comparison of specimen failure modes

从图6可知，2试件与有限元结果整体吻合情况较好;但由于试件在运输、加工的过程中发生磕碰、焊接等原因使得试件端部存在更大的初始缺陷，因此试件Q3-wb21在试件两端先发生屈曲；而试件Q3-wb11在被加劲板中部先发生局部屈曲。其他试件情况类似，限于篇幅，故不再赘述。

图7 局部稳定试件对比Fig.7 Comparison of locally stabilized specimens

2.3 极限承载力与平均应力-应变曲线验证

试件Q3-wb11、Q3-wb21的平均应力-应变曲线对比见图7，其余试件均类似。由图可知，2个典型试件的破坏现象与应力-应变曲线吻合良好，当试件进入非弹性段，试件在极限荷载状态下的平均应变均大于相应的有限元数值，说明试件实际产生较大的轴向变形，在试验过程中的轴压刚度退化更快，原因是：受焊接、切割等因素的影响，试件残余应力分布不均匀，且实际初始几何缺陷非常不规则，进而导致试件的延性较差。

表3为试验结果与有限元模拟结果对比。其中σu、σFEM分别为相应试验试件、有限元模型的极限平均应力。从表中可知，两者极限平均应力的最大差值为2.17%，整体较为接近，有限元结果比试验结果平均略小1.07%，说明该方法的正确性。

表3 极限平均应力对比Tab.3 Comparison of Limit Average Stress

3 T肋局部稳定分析

3.1 有限元模型尺寸

图8 局部模型横截面Fig.8 Cross section of local model

采用经上文验证的有限元模型，以不同的材料本构关系，焊接残余应力和局部初始几何缺陷为参数，展开参数分析。根据发生屈曲破坏的顺序不同，计算模型分为腹板(W25～W50)、翼缘(F10～F30)2组试件。对于腹板试件组，为保证腹板先发生屈曲，腹板宽厚比在25～50变化，被加劲板、翼缘的宽厚比分别保守取为18.75、10.00；对于翼缘试件组，为使得翼缘先失稳，翼缘宽厚比在10～30变化，被加劲板、腹板宽厚比均保守取为30。长度取3倍相应失稳板件宽度。有限元模型截面见图8，有限之模型尺寸见表4，取发生屈曲的子板件作为分析对象，提取其屈曲承载力，并除以板件截面面积得到极限平均应力进行分析。

表4 有限元模型尺寸Tab.4 Dimensions of finite element model

图9 不同本构关系的影响Fig.9 Influence of different constitutive relations

3.2 本构模型的影响

分别采用四折线、理想弹塑性、切线模量为0.01倍弹模(1%两折线模型)、0.03倍弹模(3%两折线模型)4种本构模型进行分析。有限元模型计入《冷弯薄壁型钢结构技术规范》(GB 510018—2002)[18]要求的局部初始几何缺陷，暂不计残余应力。不同本构模型对试件稳定承载力的影响。其中，稳定系数为试件极限平均应力与屈服强度的比值。由图9可知，2组试件的变化趋势接近，采用四折线、理想弹塑性的系数曲线基本一致；采用3%两折线的稳定系数最大，1%两折线模型次之,因此，下文分析均采用偏安全的理想弹塑性本构。

3.3 焊接残余应力

本文采用文献[17]中盲孔法测试结果，采用以折代曲的方式简化该类试件的残余应力，残余应力简化分布如图10所示。根据残余应力的自平衡原理，得到其计算公式，见式(5)、(6)。式中：σωc、σωt分别为腹板残余压、拉应力值，aω(ay)、bω(by)分别为过渡区压、拉应力长度。σyc、σyt为翼缘残余压、拉应力值。图11为分别考虑简化残余应力、数值模拟残余应力后对试件Q3-wb11、Q4-wb11稳定承载力的影响。

(a) 腹板简化分布

(b) 翼缘简化分布

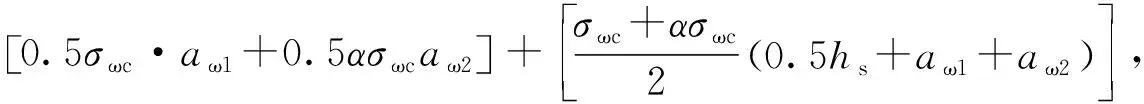
(5)

(6)

试件wb11简化残余应力验证如图11所示。由图可知，考虑2种计入结方法基本一致，因此，各试件均采用简化残余应力分布的方式进行板件的局部稳定分析，残余应力的影响如图12所示。由图12可知，相比于不考虑残余应力，考虑简化残余应力分布后的稳定承载力更小。随着板件宽厚比的增大，残余应力对试件的影响更大，当腹板宽厚比为50、翼缘宽厚比为30时，稳定系数分别折减11.1%、5.3%，因此，考虑简化残余应力分布对稳定承载力的分析会偏于安全。

图11 试件wb11简化残余应力验证Fig.11 Verification of simplified residual stress of specimen wb11

图12 残余应力的影响Fig.12 Influence of residual stress

3.4 局部初始几何缺陷的影响

由于局部缺陷本身存在的随机性，因此分别取宽厚比最大的W-50、F-30试件模型，采用一致缺陷模态法，缺陷幅值按一阶屈曲模态下子板件板宽的1/200计入。分别在T肋加劲板不同子板件处计入局部初始几何缺陷，其应力-应变曲线结果如图13所示。

(a) W-50模型

由图13可知，当T肋加劲板不同子板件分别考虑局部初始几何缺陷后，加劲板受力特征一致，平均应力-应变曲线基本重合，当宽厚比最大的子板件计入缺陷后，曲线塑性缓坡段的斜率下降得更快，即轴向刚度减小，同时极限平均应力也减小。当T肋加劲板各板件均计入局部初始几何缺陷时，相应的稳定系数最小。因此，在后文分析中，采用各子板件均施加局部初始几何缺陷的方法。

图14 不同初始缺陷幅值的影响Fig.14 Influence of different initial defect amplitudes

局部初始几何缺陷的幅值大小同样会对板件局部稳定性能存在影响。为此，在一阶屈曲模态下，按一定倍数的失稳板件宽度的计入1/50、1/100、1/200、1/300倍缺陷幅值。图14为不同幅值下，各板件宽厚比与稳定系数的变化情况。

由图14可知，当板件宽厚比相同时，随着缺陷幅值的增大，板件的稳定系数减小，变化幅度随板件宽厚比的增大，呈先增后减的趋势。当腹板宽厚比为35、翼缘宽厚比为20时，对应的稳定系数变幅最大。随着板件宽厚比的增大，将越容易出现局部失稳，导致其稳定承载力降低，故此时局部初始几何缺陷幅值影响减小。结合规范[18]的限值，下文局部初始几何缺陷幅值均考虑1/200倍的失稳板件宽度。

3.5 T肋局部失稳机理分析

由于腹板和翼缘不同的支承条件，因此以宽厚比最大的W-50、F-30的2组试件为例，通过其加载全过程中的失稳破坏模式以及承载力分布进行分析，以说明T形加劲肋的受力与破坏机理。图15、16为试件相应的变形图。

由图15中可知，极限承载力时刻，W-50构件在腹板处发生了3个波的面外变形(图15a)，在最终破坏时刻，腹板、翼缘以及被加劲板发生共同屈曲，翼缘的面外变形逐步大于腹板(图15b)；由图16可知，翼缘F30构件则在翼缘两侧各出现1个波的面外变形(图16a)，而最终破坏形态为翼缘两侧出现最大的面外变形，腹板发生较小的1个波的面外变形，被加劲板所受到的影响仍较小。

2类构件的轴向荷载-轴向位移曲线与被加劲板腹板、翼缘在加载全过程中的承载占比见图17、18。从图17可见，对于试件W-50，随着荷载的增加，各子板件逐渐达到屈服强度，整体受力开始进入非弹性阶段(图17(a)，A点)，轴向荷载-轴向位移曲线的斜率变缓。此时翼缘已达到了极限荷载，但构件的总荷载仍在增加，超过构件极限荷载后(图17(a)，B点)，但此时被加劲板仍可以承载，因此整个构件轴向荷载-轴向位移曲线的下降段并没有体现的那么明显。由图17(b)可知，此时被加劲板、腹板承受大部分荷载。随着荷载增大，被加劲板受荷占比增加，翼缘占比不断减小，腹板占比略有减小。对比图18可知，对于翼缘局部失稳模式构件，其轴向荷载-位移曲线与腹板构件趋势相同，不同的是腹板及翼缘的承载力占比较小，当超过构件极限荷载后，腹板及翼缘的荷载占比逐渐较小，被加劲板占比不断增加。

(a) W-50荷载-位移曲线

(b) W-50模型承载力占比

(a) F-30荷载-位移曲线

(b) F-30承载力占比

4 腹板局部稳定计算方法

4.1 腹板局部稳定简化计算公式

为研究T肋腹板的局部稳定承载力，分别选取Q345、Q420钢材，在仅发生腹部失稳的前提下，改变腹板高度、厚度，得到对应的T形肋加劲板试件的受压局部稳定系数。建立2种钢材强度的有限元模型共64个，模拟方法根据本文第3节所述。

图19为不同钢材强度下Q345、Q420钢材数值模拟结果与相应的多项式、Perry拟合公式曲线。其多项式公式分别见式(7)、(8)；Perry公式分别见(9)、(10)。

(7)

(8)

(9)

(10)

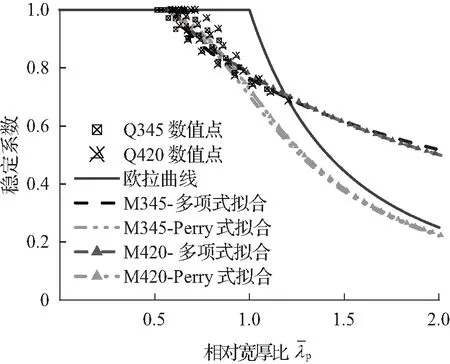
图19 腹板拟合结果Fig.19 Web plate fitting results

由图19可知，根据各有限元数值点所拟合到的多项式、Perry公式，两公式曲线接近，不同钢材对板件的稳定承载力影响较小。相比于多项式公式曲线，Perry公式曲线则更早发生折减。在相对宽厚比小于0.82时，拟合的Perry公式曲线高于多项式曲线，相应的稳定承载力更高；反之，拟合的多项式曲线更高。在整个相对宽厚比范围内，Perry公式曲线均低于欧拉曲线，而当相对宽厚比超过1.2时，多项式曲线则高于欧拉曲线，允许腹板考虑屈曲后强度的提高。

4.2 腹板稳定系数折减曲线对比

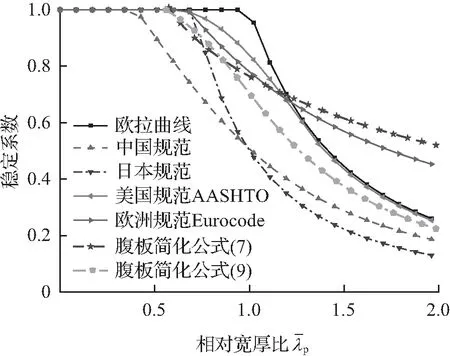
图20 各国规范曲线对比Fig.20 Comparison of national standard curves

图20为Q345拟合曲线与中国规范[15]、日本规范[19]、美国规范[20]、欧洲规范[21]对比。

由图20可知，对于中国、日本、美国规范较为保守，其局部稳定曲线整体均低于欧拉曲线，不考虑板件屈服所产生薄膜应力。对于欧洲规范，在相对宽厚比大于1.2时，曲线位于欧拉临界曲线上方，说明允许设计人员在宽厚比较大时，考虑板件薄膜应力，利用其屈曲后强度。

对于公式(7)曲线，整体接近于欧洲规范，允许板件发生局部屈曲，不同的是：该曲线在相对宽厚比较小时即开始折减，当相对宽厚比大于0.73后，公式(7)曲线位于欧洲规范曲线上方。而公式(9)曲线则较为保守，不允许板件局部失稳，相对接近于中国、美国、日本规范曲线。相比于中国规范曲线，公式(9)拟合的曲线发生折减时的相对宽厚比更大，但小于美国、日本规范曲线。

5 结论

①在本文T肋加劲板局部稳定试验与有限元模拟中，所有试件均因板件的局部变形而破坏，且有限元模型的吻合情况良好。随着腹板宽厚比的增大，试件局部变形程度增大。

②随着板件宽厚比增大，残余应力的影响逐渐增大，当腹板宽厚比、翼缘宽厚比为50、30时，稳定系数分别减小11.1%、5.3%；当T肋加劲板各组成板件均考虑局部初始缺陷时，稳定性能最差；对于T形加劲肋而言，腹板与翼缘的破坏模式有着明显差异。

③对于腹板简化公式曲线，随着相对宽厚比增加，采用多项式拟合的结果高于欧洲规范，允许考虑屈曲后强度；采用Perry公式拟合的结果则低于欧拉临界曲线，整体介于中国与美国规范之间。

④T肋加劲板的局部稳定性能对钢材不敏感，建议采用不考虑屈曲后强度的Perry公式进行设计。