基础隔震框架结构的分布参数动力模型及地震响应规律的研究*

彭凌云 刘 文 孙 睿

(北京工业大学工程抗震与结构诊治北京市重点实验室,北京 100124)

基础隔震在实际工程中的应用逐渐增多，且都具有良好的减震效果。但基础隔震建筑的上部结构和隔震层的阻尼特性有显著差距，是一种非比例阻尼体系[1-2]，对于大部分基础隔震结构，上部结构与隔震层的相互作用不能仅考虑上部结构的主频率，高阶振型对上部结构的影响也很大。在隔震结构设计时，GB 50011—2010《建筑抗震设计规范》[3]采用分部设计方法或强迫解耦的振型分解反应谱方法进行计算[4]，两者均忽略了结构非比例阻尼的影响，当隔震层阻尼逐渐增大时由此引起的误差也越来越大，更不能真实地描述基础隔震结构的动力特性，所以许多学者提出了简化计算模型来弥补这方面的不足。

文献[5-6]提出一种双自由度的等效模型，可以预测中低层隔震结构的最大地震响应。对于基础隔震结构通常采用离散的有限元模型或更简单的双自由度、多自由度等效模型[7-8]。杜永峰等采用等效的双自由度体系简化模型，对隔震体系上部结构层剪力和隔震层位移进行等效分析[9]。杜永峰等将层间剪切型结构化简为多级串联非比例阻尼隔震结构模型，并将该模型的阻尼矩阵表达形式推广至多级串联非比例阻尼模型，采用状态空间法对其进行地震响应分析[10]。但上述简化方法的应用都比较局限，而分布参数模型可以给出结构响应显式的表达形式，在研究结构动力规律方面更具优势。Skinner等将基础隔震上部结构等效为剪切梁模型，研究了经典阻尼和非经典阻尼情况下隔震结构动力特性[11]。刘平等提出基础隔震结构的分布参数剪切梁模型，并指出该模型可以更清楚、更全面地反映上部结构与基础隔震参数的相互关系[12]。潘东辉等认为高层隔震结构可简化为隔震悬臂梁模型,但并未考虑非比例阻尼对结构动力特性的影响[13]。

以基础隔震框架结构为对象，基于分布参数体系并结合结构的特点，将建立考虑非比例阻尼的分布参数剪切型悬臂梁隔震模型并求解。通过这个模型，研究固定支座、比例阻尼隔震和非比例阻尼隔震模型的动力特征，考察隔震前、后结构周期的变化以及比例阻尼隔震和非比例阻尼隔震对应的周期、阻尼比和振型参与系数。同时通过振型分解时程分析方法，对比比例阻尼隔震与非比例阻尼隔震模型的响应，一方面对比比例阻尼隔震和非比例阻尼隔震模型的响应差异；另一方面对比分部设计方法与比例阻尼隔震整体设计方法对应的模型响应。

1 基础隔震剪切型悬臂梁模型

假定基础隔震框架结构的上部为剪切型悬臂梁，隔震层刚度、阻尼和质量分别为kb、cb、mb，如图1所示。图中:u为悬臂梁相对于地面的位移;ρ、G、A分别为悬臂梁的密度、剪切模量和横截面积；l为梁的高度，下文中归一化为1。

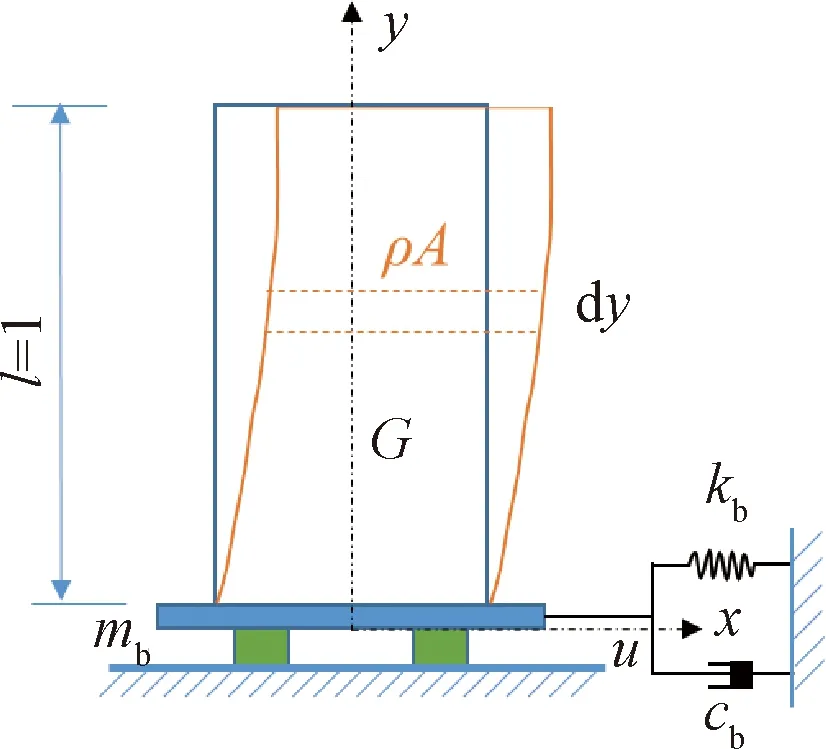
图1 剪切型悬臂梁模型Fig.1 A model of shear cantilever beams

1.1 剪切型悬臂梁模型运动方程表达式

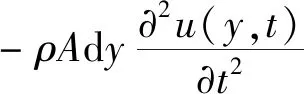
图2 微梁段隔离体Fig.2 Micro beam sections

(1)

为简化表达，上式中u=u(y,t)，下文同。假定上部结构阻尼较小且分布较为均匀，符合瑞雷阻尼假定，则微段阻尼力可分为质量相关部分和刚度相关部分，即：

fD(y,t)=fDρ(y,t)+fDG(y,t)

(2)

其中，质量与刚度相关部分表达为：

(3a)

(3b)

将式(2)代入式(1)后整理得：

(4)

由分离变量法求解方程(4)，其n阶振型对应的自由振动解具有如下形式：

un=φn(y)eλnt

(5)

式中：φn(y)为振型函数;λn为复数特征值;ζn、ωn为第n阶振型的阻尼比和频率比。

将式(5)代入式(4)可得：

(6)

式(6)表示振型求二阶导数后函数形式不变，可假定振型函数为：

φn(x)=cos[γn(l-x)]x∈[0,1]

(7)

式(7)表示的振型的顶部位移为1。将式(7)代入式(6)以后得到：

(8)

式中：γnl是剪切梁波数；α、β为Rayleigh阻尼系数。梁顶部边界条件是剪力为零，即切应变为零，式(7)表示的振型函数求一阶导数后自动满足；根据梁底部边界条件可以解得波数γnl，进而求得对应频率和振型。下面针对上部剪切梁底部分别为固定支座边界、自由支座边界和隔震支座边界条件进行讨论。

1.2 固定支座边界条件

当梁底部固定时，其边界条件为cos(γfbnl)=0，其中下标fb表示固定支座，n表示第n阶振型，可得：

γfbnl=(2n-1)π/2n=1,2,3…

(9)

比例阻尼条件下，其振型与无阻尼条件结果相同，令α、β为0，式(8)可简化为：

(10)

可得固定支座条件的第n阶振型的频率为：

(11)

1.3 隔震支座边界条件

当上部剪切梁底部布置隔震支座时，底部边界剪力平衡条件为：

(12)

式中：φbn是第n阶振型隔震层相对于地面的位移。

其振型函数形式同式(7)，当x=0时有φbn=cos(γnl)。定义隔震结构第n阶复振型特征值为：

λn=λιnωfb1

(13)

ιn=ωn/ωfb1

式中：ωfb1为固定支座边界条件下隔震结构的第一阶振动频率；ιn为隔震结构的振型频率比。

将式(7)代入式(12)右端求积分可得：

(14)

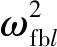
(15)

式中：μ、ζb、κ、αm分别为隔震层质量比、阻尼比、隔震系数和无量纲瑞雷阻尼质量系数。

μ、ζb、κ、αm的计算式分别为：

(16a)

(16b)

(16c)

(16d)

即把隔震层上部结构当做单自由度的隔震频率。式(15)表明：隔震结构的振型频率比、阻尼比依赖于上部结构阻尼系数αm和隔震层参数ζb、κ、μ，而与上部结构振型频率绝对值无关。

将式(13)代入式(7)可求得用复特征值和固定支座条件时第一振型波数表示的隔震结构波数计算式：

(17)

其中βk=βωfb1

式中：βk为无量纲瑞雷阻尼刚度系数。

将式(17)代入式(15)，当上部结构比例阻尼系数和隔震层参数已知时，令实部、虚部相等即可获得关于ζn、ιn的超越方程组，一般情况下需采用数值方法求解该方程组。将阻尼比和频率比的解代入式(17)和式(7)即可得到各阶波数和复振型。

1.4 复振型的正交性

参考离散模型复振型正交性的定义，当j不等于k时，分布参数模型的复振型满足：

(18a)

(18b)

式中:积分包含了边界条件[14]，φj、φk分别为第j、k阶振型的隔震层相对于地面的位移，与质量相关部分需加上φbjmbφbk，φbj、φbk分别为第j、k阶振型的隔震层位移分量，与刚度相关部分按分部积分公式做如下变换：

(19)

式(19)右边第一项的物理意义为：当GA=1时，第k阶振型底部剪力在第j阶振型底部自由度做的虚功，代表底部隔震层弹性支座对正交性的贡献。

1.5 不考虑阻尼的振型分解

当不考虑阻尼时，式(17)变换为λιn=iιn，式(15)和式(17)分别变换为如下形式：

(20)

式中：ιn和γn都是实数。

γnl=γfb1ιn

(21)

将式(21)代入式(20)后可求得τn，然后代入式(8)可得到振型函数。

1.6 振型阻尼比的强迫解耦方法

(22)

据式(8)可得上式中的积分式为：

(23)

2 基础隔震框架结构地震响应

地震作用下，式(1)中惯性力部分的增加地面运动加速度分量。相应的，式(4)变为如下形式：

(24)

参考离散模型复振型参与系数的定义，按照前述正交条件可得到分布参数模型复振型参与系数的计算式为：

(25)

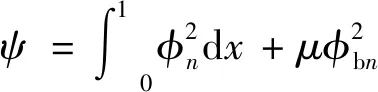
不考虑阻尼影响时的振型参与系数计算式为：

(26)

文献[16]给出地震作用下采用复振型表示的位移响应计算式为：

(27)

其中un=2Re[ηnδn(t)φn]

式中:ηn、φn为复数形式的振型参与系数、振型向量；δn(t)为第n阶振型复数形式的响应时程；un为第n阶振型对应的位移，为实数。

分布参数模型有无数振型，按照振型分解理论，取有限阶振型组合即可。

第n阶振型复数形式的响应按一阶系统杜哈梅公式求解如下：

(28)

利用欧拉公式和单自由度系统杜哈梅积分公式可得：

(29)

代入式(27)可得到：

(30)

与比例阻尼系统振型分解相比，考虑非比例阻尼的振型分解对应响应包含了速度项。当系统退化为比例阻尼时，速度项中Re(ηnφn)为0(因为比例阻尼系统的ηn实部为0，φn虚部为0)，式(30)将退化为比例阻尼系统的振型分解式。

剪切型分布参数结构的截面剪力为GA与位移函数一阶导数的乘积，与式(30)对应的截面剪力计算式为：

(31)

分布参数结构的层间位移角等于位移函数的一阶导数：

(32)

3 基础隔震框架结构动力特征分析

基于基础隔震剪切型悬臂梁模型，研究固定支座模型、比例阻尼隔震和非比例阻尼隔震模型的动力特征。考察了隔震前后结构周期及振型的变化，同时对式(17)、(15)、(25)和式(20)、(22)、(26)表示的非比例阻尼隔震(考虑阻尼影响)和比例阻尼隔震(不考虑阻尼影响)求得的频率、阻尼比和振型参与系数的结果加以对比分析。

比例阻尼隔震和非比例阻尼隔震模型分别采用强迫解耦方法和复振型分解方法计算。

算例计算参数如下：上部结构前两阶振型的阻尼比为0.05，计算得到无量纲的瑞雷阻尼系数αm和βk分别为0.075和0.025；隔震系数κ=0.5、隔震层质量比μ=0.1，隔震层阻尼比ζb=0.2；隔震前结构周期为1.5 s。

3.1 隔震前后结构周期及阻尼比对比

根据式(12)、(17)、(20)求固定支座(隔震前)以及隔震支座边界条件下的周期，固定支座边界条件下采用实振型解耦方法计算；隔震支座边界条件下按强迫解耦和复振型分解方法计算。

表1给出了基础隔震剪切型悬臂梁模型在隔震前后相应的前六阶振型周期计算结果。

表1 剪切型悬臂梁模型周期对比Table 1 The contrast to periods of the shear cantilever beam model s

从表中可以看出：1)基础隔震显著延长第一阶振型周期，对高阶振型周期影响逐步减小，该现象及其原因可参考文献[11]。2)采用复振型分解计算的振型周期结果与不考虑阻尼实振型差别较小。

图3给出了当隔震系数κ取0.3～1.0，隔震层阻尼比ζb取0.05～0.25时，实振型强迫解耦计算的前四阶振型阻尼比相对于复振型分解计算结果的误差结果。

a—一阶振型阻尼比误差；b—二阶振型阻尼比误差；c—三阶振型阻尼比误差；d—四阶振型阻尼比误差。图3 两种阻尼比计算相对误差Fig.3 The relative errors of damp ratios between calculated by the proportional damping model and by the non-proportional damping isolated model

图3中误差为复振型分解方法与强迫解耦方法计算结果的差除以复振型分解方法计算结果。可知，当隔震层阻尼参数保持不变，隔震系数κ从0.3递增至1.0时，强迫解耦模型前4阶振型对应的阻尼比相对误差也逐渐增大；当隔震系数保持不变，隔震层阻尼比ζb从0.05递增至0.25时，模型前四阶振型对应的阻尼比相对误差逐渐减小，总体误差不超过10%。

上述结果表明，随着隔震层阻尼比及隔震系数的增大，强迫解耦方法与复振型分解方法的计算误差也相应增大，但总体上区别不大。

3.2 隔震前后结构振型对比

图4给出了剪切型悬臂梁模型在隔震前后前三阶振型的对比情况。隔震支座边界条件下采用复振型分解方法计算，复振型实部与虚部分开作图。

强迫解耦；复振型实部；复振型虚部；固定支座;b为隔震层所在位置。图4 不同支座情况下前三阶振型对比Fig.4 Comparisons of the first three modals with different supports

由图4可以看出：1)强迫解耦方法振型与复振型分解方法振型实部接近，但强迫解耦方法忽略了虚部对振型的影响，计算结果偏小。2)复振型虚部绘制的振型曲线符合一般规律，但其绝对数值明显小于实部，对模型振型的影响较小。3)基础隔震结构的受力特点与固定支座结构明显不同，结构设计时需要考虑振型的影响。

4 隔震前后结构地震响应特征

4.1 隔震前后振型参与系数对比

表2给出了固定支座结构及根据式(25)和式(26)计算的比例阻尼隔震和非比例阻尼隔震模型前四阶振型的振型参与系数。

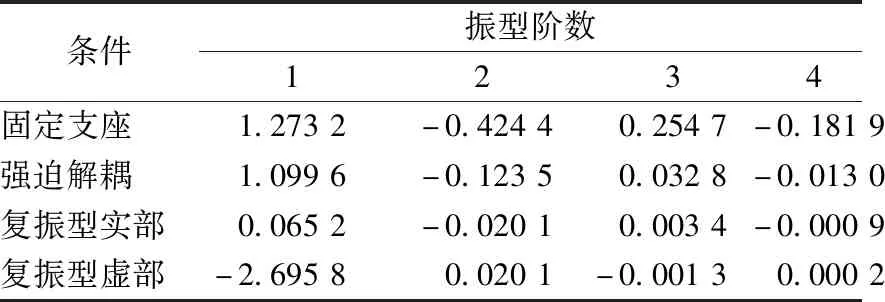
表2 隔震前后振型参与系数对比Table 2 Comparisons of modal participation coefficients before and after being isolated

由表2可知，基础隔震显著降低了结构高阶振型参与系数，且复振型分解方法的振型参与系数随振型阶数的增加而快速减小，第四阶时振型参与系数已衰减至0.000 1；强迫解耦方法的振型参与系数变化规律和复振型分解方法一致。

虽然3.1节分析结果显示基础隔震对高阶振型周期影响较小，但由于其有效降低了结构高阶振型的振型参与系数，因而是可以对高阶振型起到显著减震效果的。

4.2 隔震前后楼层剪力分布规律

结构计算参数同第3节算例，图5给出了隔震前后结构前三阶振型的层剪力分布规律。

a—振型1；b—振型2；c—振型3。 强迫解耦；复振型实部；复振型虚部；固定支座。图5 隔震前后层剪力分布Fig.5 Floor shear distribution before and after being isolated

隔震支座边界条件下分别采用强迫解耦方法和复振型分解方法计算结构振型层剪力。由图5可知，隔震后结构的层剪力分布与固定支座结构明显不同。

4.3 分部设计方法与整体设计方法对比

本节通过振型分解时程分析方法，对比分部设计方法与整体设计方法(比例阻尼隔震模型)计算的结构响应；同时比较比例阻尼隔震模型与非比例阻尼隔震模型响应。

算例计算参数如下：分部设计方法的上部结构基本周期为1.5 s、瑞雷阻尼为0.05；包含隔震层的整体结构的隔震层隔震系数κ=0.5，质量比μ=0.1，隔震层阻尼比ζb=0.2；输入的地震动数据采用美国应用技术委员会(ATC)报告[17]建议的22条远场地震波和28条近场地震波，分别为EQ01～EQ22和JEQ01～JEQ28，地震动峰值加速度调整为0.1g。

由分部设计方法及整体设计方法计算结构振型剪力，得出该算例的楼层剪力分布规律，如图6所示。

a—分部设计方法楼层剪力；b—整体设计方法(比例阻尼隔震模型)楼层剪力。左图为上部结构在各个时程下对应的层剪力/总重力的数值；右图为将左图各时程对应的值以底部最大值作为基准做归一化处理。图6 分部设计方法与整体设计方法楼层剪力Fig.6 The floor shear force of the division design method and the integral design method

图6可知，整体设计方法(比例阻尼隔震模型)与分部设计方法计算的层剪力均随结构高度的增加而逐渐减小，整体设计方法的楼层剪力计算结果约为分部设计方法的1/4。

将各时程对应的层剪力进行底部对齐处理后，分部设计方法与时程方法计算均值较为吻合，而整体设计方法计算的剪力值由于受高阶振型的影响相比于时程均值离散情况更为明显，且计算结果偏小。这也是因为基础隔震对结构振型参与系数的影响较大，且隔震前后结构受力显著不同，所以导致分部设计方法与整体设计方法计算的结果有明显差异。

图7给出了不考虑非比例阻尼的整体隔震模型与考虑非比例阻尼的整体隔震模型的楼层剪力计算结果对比。结果表明：不考虑非比例阻尼时的计算结果比考虑非比例阻尼时的计算结果偏小，二者最大差值为22.75%，所以用包含隔震层的整体模型进行计算时，应考虑非比例阻尼的影响。

比例阻尼隔震；-----非比例阻尼隔震。图7 比例阻尼隔震与非比例阻尼隔震模型楼层剪力对比Fig.7 Comparisons of floor shear forces between calculated by the proportionally damped model and by the non-proportionally damped isolation model

5 结束语

基于分布参数体系并结合基础隔震框架结构的特点，介绍了考虑非比例阻尼的分布参数悬臂梁隔震模型的建立及求解过程。基于此模型，通过算例分析得出如下结论：

1) 复振型分解方法和实振型分解方法在求解隔震结构的动力特征方面差别较小。基于实振型的强迫解耦方法计算隔震结构响应结果偏小，其原因是不考虑隔震层非比例阻尼导致漏算了速度部分的贡献。

2) 隔震层对高阶振型周期的影响有限，但可有效降低结构高阶振型的振型参与系数。

3) 基础隔震结构与固定支座结构的振型、振型参与系数及层剪力存在显著差异，采用分部设计方法计算的楼层剪力分布与非比例阻尼方法计算整体模型结果存在一定的差异，不过误差较小。

对于剪切型基础隔震结构的设计，采用分部设计方法也是合适的，对于其他类型结构则需另做讨论。若采用包含隔震层的整体模型进行分析，则建议采用考虑非比例阻尼特征的复振型分解方法。