钢-聚丙烯混杂纤维陶粒混凝土与螺纹钢筋的黏结力学特性*

朱红兵 张 娜 余志武 蒋丽忠 徐文康

(1.武汉科技大学城市建设学院,武汉 430065；2.高速铁路建造技术国家工程实验室，长沙 410075)

陶粒混凝土具有轻质高强、绿色环保、耐火抗冻等优点，具有广阔的应用前景[1]。陶粒混凝土与钢筋的黏结性能，对陶粒混凝土结构性能会产生很大影响[2]。在混凝土中掺入纤维能有效改善混凝土材料的韧性，减少混凝土结构裂缝的生成和扩展，改善混凝土与钢筋之间的黏结性能[3]。将几何尺寸较大、弹性模量高的钢纤维和几何尺寸较小、弹性模量低的聚丙烯纤维按一定比例混掺，形成刚柔结合的乱向分布空间三维网，依靠聚丙烯纤维桥接混凝土内的微裂缝并抑制其扩展，利用钢纤维的桥接作用控制宏观裂缝，可使聚丙烯纤维和钢纤维在混凝土破坏过程中的不同层次、不同阶段上体现增强增韧作用[4-6]，产生正混杂效应。

钢-聚丙烯混杂纤维能改善混凝土与钢筋的黏结性能，提高结构的延性[7-8]。目前，对于钢-聚丙烯混杂纤维陶粒混凝土的研究多集中于纤维对陶粒混凝土基本力学性能的改善，钢-聚丙烯混杂纤维陶粒混凝土与钢筋的黏结性能还不明晰[9-10]。文献[1，11]介绍了对钢纤维陶粒混凝土与高强轻骨料混凝土黏结性能的研究，建立了相应的混凝土极限黏结强度计算式。Aslani等通过试验建立了自密实混凝土黏结强度计算式[12]。现有文献的黏结强度计算式大都未考虑纤维对黏结强度的影响，文献[11]虽考虑了钢纤维掺量，但钢-聚丙烯混杂纤维所体现的混杂效应较单掺钢纤维更加复杂。变形钢筋与混凝土的黏结滑移关系多采用平均黏结应力-滑移本构关系来表达，常采用基于试验建立的分段函数半理论模型表达式。欧洲标准CEB-FIP[13]中给出的分段模型分为上升段、水平段、下降段和残余段。叶列平等提出了高强轻骨料混凝土黏结-滑移曲线分段式模型[1]，主要由上升段和下降段组成。

通过对16组不同掺量的钢-聚丙烯混杂纤维陶粒混凝土试件进行抗压劈裂及拉拔试验，得出不同混杂纤维掺量混凝土与钢筋之间的黏结强度，并进一步得到钢-聚丙烯混杂纤维混凝土与钢筋间黏结的应力-应变关系。

1 钢-聚丙烯混杂纤维陶粒混凝土

1.1 原材料

采用华能牌束状单丝聚丙烯纤维SHWITCOM端勾型钢纤维，物理性能指标见表1和表2。

表1 聚丙烯纤维物理力学性能指标Table 1 Physical and mechanical properties of polypropylene fibers

表2 钢纤维物理力学性能指标Table 2 Physical and mechanical properties of steel fibers

粗骨料采用宜昌光大牌900级碎石型页岩陶粒，见表3。陶粒在使用前先预湿处理。细骨料采用天然河沙，堆积密度为1.56 t/m3,细度模数为2.65，含泥量小于2%，使用前过4.75 mm方孔筛筛分。水泥采用湖北华新公司生产的P·O 42.5水泥，密度为3.15 t/m3。减水剂采用青岛虹厦生产的高性能聚羧酸减水剂。

表3 页岩陶粒物理性能指标Table 3 Physical properties of shale ceramsite

1.2 混凝土配合比

参考JGJ 12—2006《轻骨料混凝土结构技术规程》，经多次试配，确定混凝土基准配合比(表4)，其中砂率为40%。

表4 混凝土基准配合比Table 4 Proportion of reference concrete mix kg/m3

参照CECS 38∶2004《纤维混凝土结构技术规程》，钢纤维体积率分4种水平考虑：0%、0.5%、1.0%、1.5%。聚丙烯纤维体积掺量采用4种水平：0%、0.6%、1.0%、1.4%[14-15]。采用不同的钢纤维(SF)及聚丙烯纤维(PP)掺量，制作16组(每组3个)100 mm×100 mm×100 mm立方体试块，标养28 d后进行立方体抗压强度和劈裂抗拉强度试验。

1.3 基本力学性能试验

立方体抗压强度、劈裂抗拉强度试验结果如表5、表6所示。

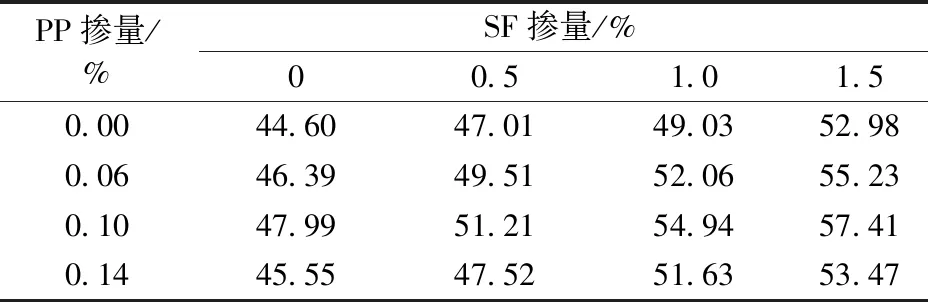
表5 钢-聚丙烯混杂纤维陶粒混凝土立方体抗压强度Table 5 Cubic compressive strength of ceramsite concrete with hybrid fibers of steel and polypropylene MPa

表6 钢-聚丙烯纤维陶粒混凝土立方体劈裂抗拉强度Table 6 Tensile strength of cube splitting for ceramsite concrete with hybird fibers of steel and polypropylene MPa

由表5、6可知：当采用同一聚丙烯纤维掺量时，试件抗压强度及劈裂抗拉强度均随着钢纤维体积率的增大而增加；钢纤维掺量相同时，随聚丙烯纤维体积率的增加，强度呈现先增大后降低的趋势，在聚丙烯纤维(PP)体积率为0.1%时达到最大值。钢纤维因其较高的弹性模量和几何尺寸，在增强混凝土强度中占主导作用，增强作用远大于聚丙烯纤维。

2 黏结性能试验

2.1 拉拔试验设计

2.1.1拉拔试件制作

采用中心拉拔试件进行钢-聚丙烯混杂纤维混凝土黏结性能试验。对于拉拔试件的尺寸各试验标准并无统一规定，现行GB/T 50152—2012《混凝土结构试验方法标准》中并未提及黏结性能的试验方法，试验参照GB/T 50152—1992要求制作。

试件的边长决定保护层厚度大小，进而会影响拉拔试件的破坏形态，在保护层厚度较小时，尚未完全发挥出材料的黏结性能就发生劈裂破坏。同时，较小的截面尺寸会使掺加的纤维产生“边壁效应”，影响纤维的均匀分布。采用武钢生产的直径d为14 mm的HRB400E钢筋。立方体试件边长取10d(140 mm)。钢筋有效黏结长度为5d(70 mm)，为消除试件因加载端局部受压影响混凝土的黏结强度，在钢筋的有效黏结区两端各设置2.5d(35 mm)的非黏结区。非黏结区采用直径25 mm的聚氯乙烯套管，钢筋与套管之间采用泡沫胶进行填充。钢筋伸出混凝土自由端和加载段的长度分别为20，300 mm。钢筋放置于立方体试件的中轴线上，在浇筑试件时钢筋纵轴应与浇筑面平行，且与拉拔试件加载承压面垂直，并进行固定。

在拉拔试件中，钢纤维的掺入能起到类似于箍筋的横向约束作用，为减少相关因素对试验的干扰，试验中的试件均未配制箍筋。拉拔试件按掺入的混杂纤维情况分为16组(每组3个试件，共48个试件)。拉拔试件的制作及试件模具见图1。

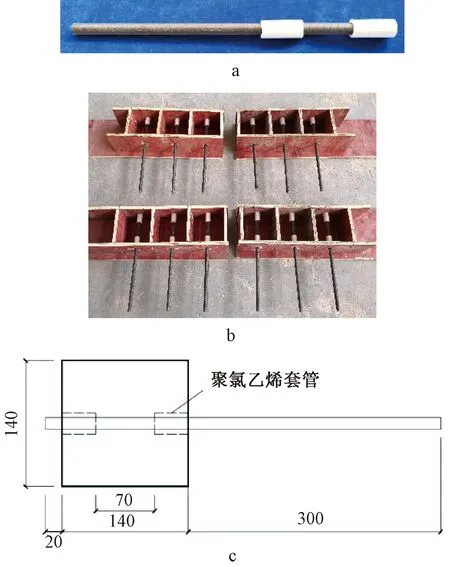
a—拉拔试件钢筋；b—拉拔试件模具；c—拉拔试件示意。图1 拉拔试件制作 mmFig.1 Specimen-making for pull-out tests

2.1.2加载装置及步骤

考虑到采用高强陶粒混凝土时，在试件破坏前自由端钢筋难免会出现较大伸长量或屈服，会对加载端滑移值产生较大影响。而自由端滑移值较加载端相对滞后，受钢筋屈服影响较小。试验以自由端滑移值作为相对滑移，在钢筋自由端底部安装一组位移计，位移传感器的精度为2.0×10-4mm。为了便于在试件自由端安装位移计固定支座，在试件自由端用AB胶将一块角钢固定在混凝土表面。采用微机控制电液伺服万能试验机(WAW-1000)加载，加载反力装置为自行设计的反力架。荷载-滑移曲线中的滑移值由位移计每两秒记录一次，荷载采用万能试验机自动记录保存。

参照GB/T 50152—1992，拉拔试验的加载速度为0.098 kN/s。试验装置示意见图2。

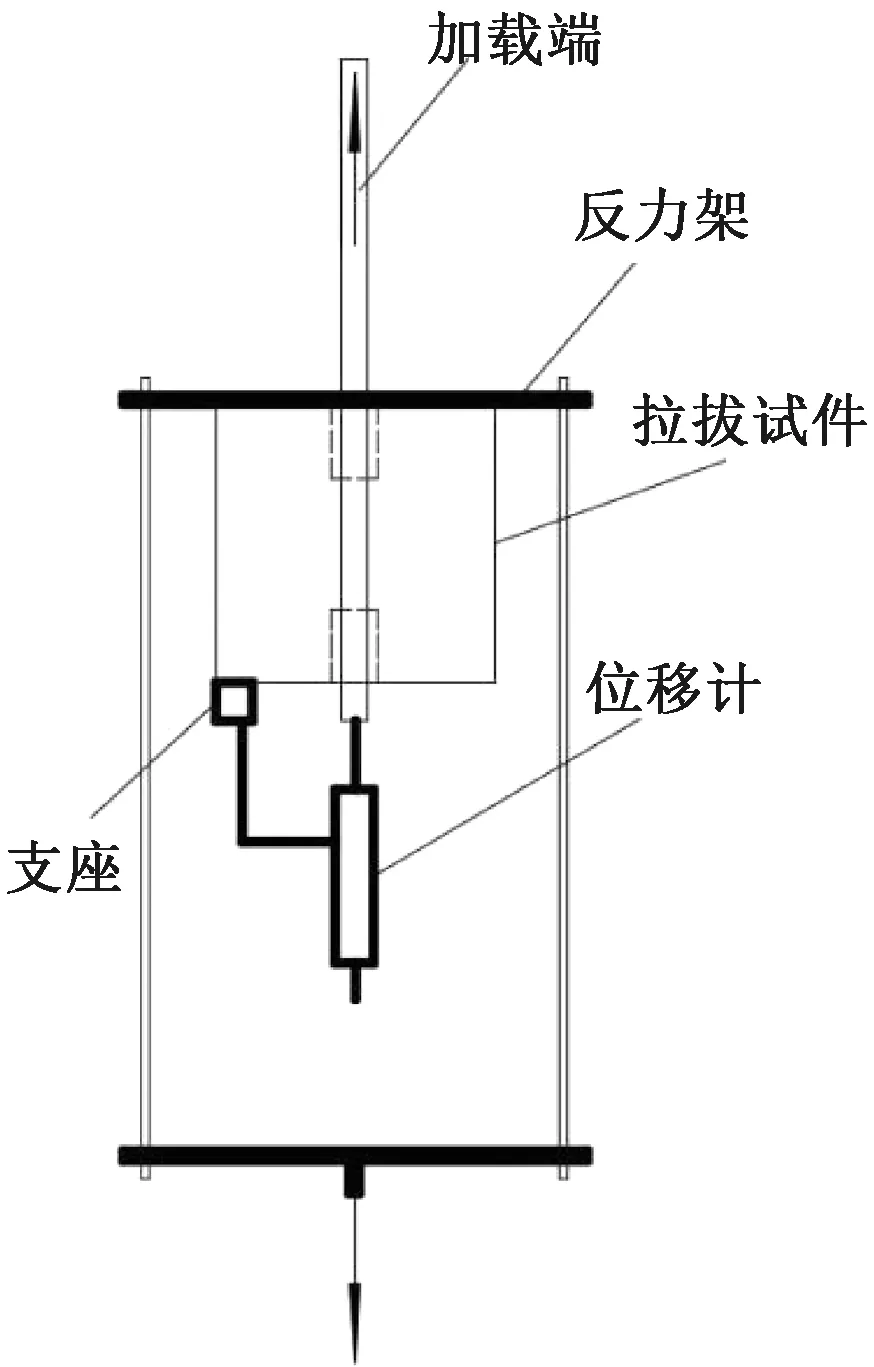
图2 拉拔试验装置Fig.2 Devices of pull-out tests

2.2 试验结果

试验所测得极限黏结强度及峰值滑移值如表7所示，每组3个试件的峰值荷载最大值和最小值与中间值之差均小于中间值的15%，表中所列的极限黏结强度τu为每组3个试件的平均值，峰值滑移su为每组3个试件的中值滑移。极限黏结强度采用有效黏结段内的平均黏结强度来表示，如式(1)所示。

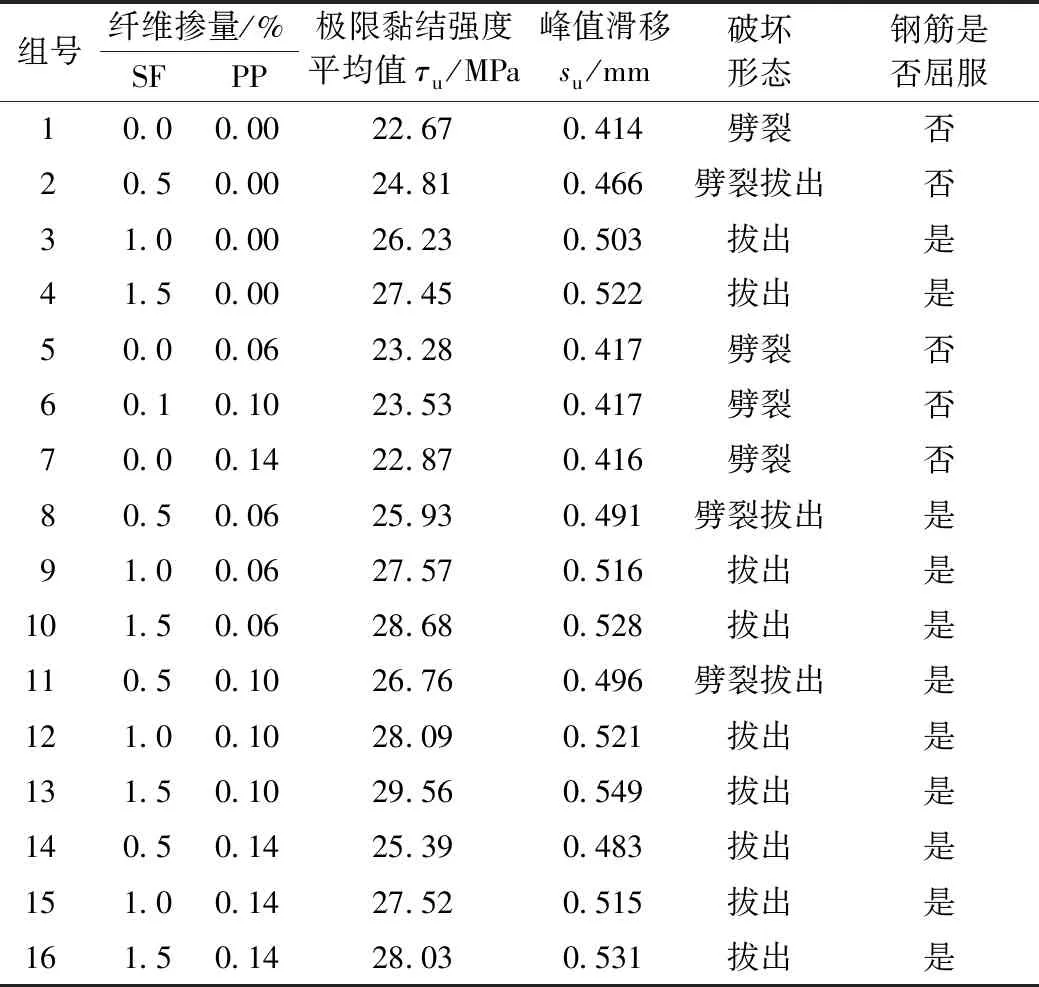
表7 拉拔试验结果Table 7 Pull-out test results

(1)

式中：Fu为峰值荷载；d为钢筋直径；l为黏结长度。

由表7可知，使用单掺钢纤维时，陶粒混凝土与钢筋的黏结性能具有明显的改善，黏结强度和峰值滑移随着钢纤维体积率的增加而增加。在钢纤维体积率为0.5%、1.0%、1.5%时，黏结强度较未掺纤维的试件分别提升9%、16%、21%，峰值滑移最大提升26%，试件由脆性破坏逐渐转向延性破坏。单掺聚丙烯纤维时，陶粒混凝土与钢筋的黏结性能也有一定的改善，随掺量增加黏结强度呈现先增大后降低的趋势，在体积率为0.1%时达到最大值。掺加混杂纤维时，如聚丙烯纤维掺量一定，黏结强度及峰值滑移随钢纤维掺量增大呈现增大；如钢纤维掺量一定，则黏结强度及峰值滑移随聚丙烯纤维掺量增大呈现先增大后减小。总体而言，掺加钢纤维及聚丙烯纤维均能改善陶粒混凝土与钢筋的黏结性能，但钢纤维的改善效果更明显。

单掺钢纤维掺量低于1%或单掺聚丙烯纤维时，试件表现为劈裂或劈裂拔出破坏形态，钢筋不屈服；单掺钢纤维掺量达到或大于1%时则表现为拔出破坏，钢筋也会处于屈服状态。混掺纤维时，除8和11两组为劈裂拔出外，其余组均为拔出破坏，混掺时钢筋均达到屈服状态。综合表6数据，试件出现劈裂破坏、钢筋未屈服的试验组，原因为纤维(尤其是钢纤维)掺量较低，混凝土的劈裂抗拉强度均较低，拉拔试件中混凝土达到劈裂抗拉强度时钢筋与混凝土之间的黏结力尚未达到极限值、钢筋拉应力也低于屈服应力。混凝土劈裂抗拉强度增大后，试件中钢筋与混凝土的黏结力才能充分发挥，破坏形态相应地变为拔出破坏。

3 黏结强度计算式及应变关系

3.1 混杂纤维陶粒混凝土黏结强度计算式

叶列平提出的针对高强陶粒混凝土的黏结强度计算式[1]为：

式中：τu为极限强度；d为钢筋直径；c为混凝土保护层厚度；la为黏结长度；ρsv为配箍率；fcu为立方体抗压强度。

文献[4，16]对混杂纤维或钢纤维混凝土梁的抗剪和抗弯性能研究认为：在中低配箍率的情况下，钢纤维或混杂纤维梁能获得更好的力学性能和变形性能，采用钢纤维或混杂纤维部分代替箍筋可增大箍筋间距，具有一定的可行性。在拉拔试件中掺入钢-聚丙烯混杂纤维能发挥出类似箍筋的作用，具有较好的护筋效果。

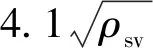
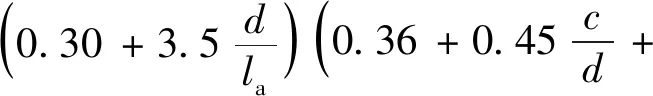
(3)

式中：fcu为未掺加纤维的陶粒混凝土立方体抗压强度；λsf、λpf分别为钢纤维和聚丙烯纤维特征参数，其值为纤维体积率与长细比的乘积；α1、β1、γ1分别为钢纤维、聚丙烯纤维以及钢-聚丙烯混杂纤维的黏结强度影响系数；δ1为强度修正参数。

采用表5及表7中的试验数据，对式(3)进行拟合，获得各参数拟合值，见表8。

表8 式(3)参数的拟合值Table 8 Fitting values of parameters in formula (3)

R2为决定系数。

3.2 混杂纤维陶粒混凝土黏结滑移模型

综合考虑以上各现有模型的特点[1,16]，兼顾黏结滑移曲线特征及算式的简化，采用三段式的表达式来描述钢-聚丙烯混杂纤维陶粒混凝土的黏结滑移模型。在残余荷载阶段，钢筋与混凝土间已发生较大的滑移，此时混凝土结构与钢筋的黏结已濒临失效，故黏结模型中未对其进行表述。表达式分为上升段、水平段、下降段，各段的表达式为：

(4)

试验测得的黏结滑移曲线显示，钢-聚丙烯混杂纤维陶粒混凝土的劈裂滑移值scr并不明显，随纤维掺量变化的影响较小。参照文献[1]的处理方法，对试验实测的黏结滑移曲线(图3)中的数据进行分析，取scr=0.017d，未掺加纤维的陶粒混凝土峰值滑移取su0=0.029 6d。峰值滑移值su按式(5)进行计算。极限黏结强度τu采用式(3)进行计算。

试验曲线；计算曲线。图3 计算模型与试验曲线对比Fig.3 Comparisons of curves from the calculation model and the test

su=su0(α2Vsf+β2Vpp+γ2VsfVpp)

(5)

式中：Su0为未掺加纤维的陶粒混凝土峰值黏结滑移值；Vsf、Vpp分别为钢纤维体积率和聚丙烯纤维体积率；α2、β2、γ2分别为钢纤维、聚丙烯纤维以及混杂效应对峰值滑移的影响系数，拟合得α2=0.199、β2=0.384、γ2=-0.101，R2=0.89。

对试验数据进行拟合得黏结滑移模型中各参数值，见表9。

表9 黏结滑移曲线参数a、b取值Table 9 Parameters a and b in the bond slip curves

考虑到实际工程中纤维掺量可任意取值，根据表9的参数值，建立钢-聚丙烯混杂纤维陶粒混凝土黏结滑移曲线上升段及下降段参数a和b的任意计算式，见式(6)，该式中各参数的拟合值见表10。

表10 黏结滑移曲线拟合参数Table 10 Fitting parameters of bond slip curves

a=α3Vsf+β3Vpp+γ3VsfVpp+δ3

(6a)

(6b)

式中：α3、β3、γ3分别为钢纤维、聚丙烯纤维以及混杂效应对黏结滑移的影响系数；Vsf、Vpp分别为钢纤维体积率和聚丙烯纤维体积率；δ3为纤维陶粒混凝土黏结滑移曲线参数的修正系数。

根据式(3)和黏结滑移模型，对钢纤维体积掺量为1.5%、聚丙烯纤体积维掺量为0.1%的陶粒混凝土黏结模型进行计算，发现计算模型与试验曲线吻合度较好，能准确地反映钢-聚丙烯混杂纤维陶粒混凝土与钢筋的黏结滑移关系。计算模型与试验结果的对比如图3所示。其余试件试验结果与计算模型曲线吻合度也较高。

4 结束语

1)16组不同钢-聚丙烯混杂纤维掺量的陶粒混凝土立方体抗压强度、劈裂抗拉强度的试验表明，采用相同聚丙烯纤维掺量时，试件强度随钢纤维体积率增大而增加；钢纤维掺量相同时，试件强度随聚丙烯纤维体积率增加，强度呈现先增大后降低的趋势。钢纤维和聚丙烯纤维体积率分别为1.5%和0.1%时，混凝土力学性能较好。

2)聚丙烯纤维掺量一定，黏结强度及峰值滑移随钢纤维掺量增大而增大；钢纤维掺量一定，则黏结强度及峰值滑移随聚丙烯纤维掺量增大呈现先增大后减小。掺加钢纤维及聚丙烯纤维均能改善陶粒混凝土与钢筋的黏结性能，但钢纤维的改善效果更明显。

3)基于试验实测黏结强度，建立了钢-聚丙烯混杂纤维陶粒混凝土极限黏结强度计算式，该式考虑了未掺加纤维时陶粒混凝土立方体抗压强度、钢纤维和聚丙烯纤维特征参数(纤维体积率与长细比的乘积)、钢筋直径、混凝土保护层厚度、黏结长度等参数。

4)基于试验实测黏结强度和滑移值，采用三段式表达式(上升段，水平段、下降段)建立了可描述钢-聚丙烯混杂纤维陶粒混凝土与变形钢筋的黏结滑移模型。