引导提出数学问题对教师教学的要求

【摘  要】  在教学设计及课堂实施时，引导学生提出合适数学问题的主导责任在数学教师，教师需要自觉自愿地发挥自己在数学教学中的主导作用，首先应该发展自己面临外在信息时提出合适数学问题的能力.在具体数学知识点的教学设计及课堂实施中引导学生提出合适数学问题时，数学教师需要依据一惯性与连续性、差异性与适应性、期待性与鼓励性三项要求.

【关键词】  提出数学问题；教学设计；三项要求

发生认识的心理动力在于对外在客观对象性信息的好奇心与兴趣，好奇心与兴趣生成了学习主体的探究与思考，如此，学也就起源于思，思起源于疑.学习主体要消解疑问所带来的心理紧张情绪，他的疑问就要获解，从而导致疑转化为学习主体所提出的问题.由此认识，可以将问题界定为：问题指的是相对于学习主体探究信息意义的新颖度与其经验的适应度存在着差距，从而无法形成共振或耦合进而出现的一些引起学习主体无法确定正确与否的信息轮廓.问题的出现在于当学习主体依据自己的经验、知识不能解释自己所面临的信息时所产生的心理困惑.本文探究数学教师通过自己的教学设计及课堂实施帮助学生提出合适数学问题的几项要求.

1  在课堂实施中坚持一惯性与连续性要求

在教学设计及课堂实施（甚至于在课外）活动中，数学教师培养学生的任何一项能力都需要坚持一惯性与连续性要求，培养学生提出合适数学问题能力当然不可能例外.这种要求就是从空间的广度上与时间的长度上，濡化熏染学生，为学生创造发展提出合适数学问题能力的学习氛围，使培养学生的数学能力始终处于“润物细无声”的背景中.

所谓一惯性指的是，数学教师在空间上所安排的教学活动都要以培养学生提出合适数学问题能力为目标导向，那么，在设计帮助学生发生具体数学知识点认识的教学活动中，或在讲解巩固知识的例题中，或在选择习题布置给学生作业中等，都要将启发或诱导学生提出合适数学问题作为一项重要环节，而不是只重视其中的某一项内容（例如，只在引导学生发生具体数学知识认识时培养学生提出数学问题能力，而在例习题中则不将启发学生提出数学问题作为一项教学目标）的教学活动，不能顾此失彼，有所偏废.

所谓连续性指的是培养学生提出合适数学问题能力，不是一朝一夕的事情，而是长年累月持久的事情，决不能浅尝辄止，因此，教师必须坚持不懈地长期努力，持之以恒（而不能三天打鱼两天晒网，或者一曝十寒地展开数学教学活动），如此，才有可能实现培养学生提出合适数学问题能力.启发学生提出合适数学问题的连续性非常重要，这是由数学知识的结构性所产生数学知识点之间的广泛联系决定的.

因此，数学教师坚持一惯性与连续性的教学活动非常重要，因为只有如此，才能形成一种合力，保证从全方位、宽领域、综合性地从总体上培养学生的数学能力，培养学生提出合适数学问题的能力当然也内涵于其中.例如，关于发生勾股定理这个知识点认识的教学设计及课堂实施，笔者是这样启发学生提出合适数学问题的：通过教材分析认识到，勾股定理来源于使用面积表示两数差的完全平方公式，于是，笔者以两数和的完全平方公式为初始问题，然后，要求学生在展开中提出合适的数学问题，从而帮助学生发生勾股定理这个知识点的认识.

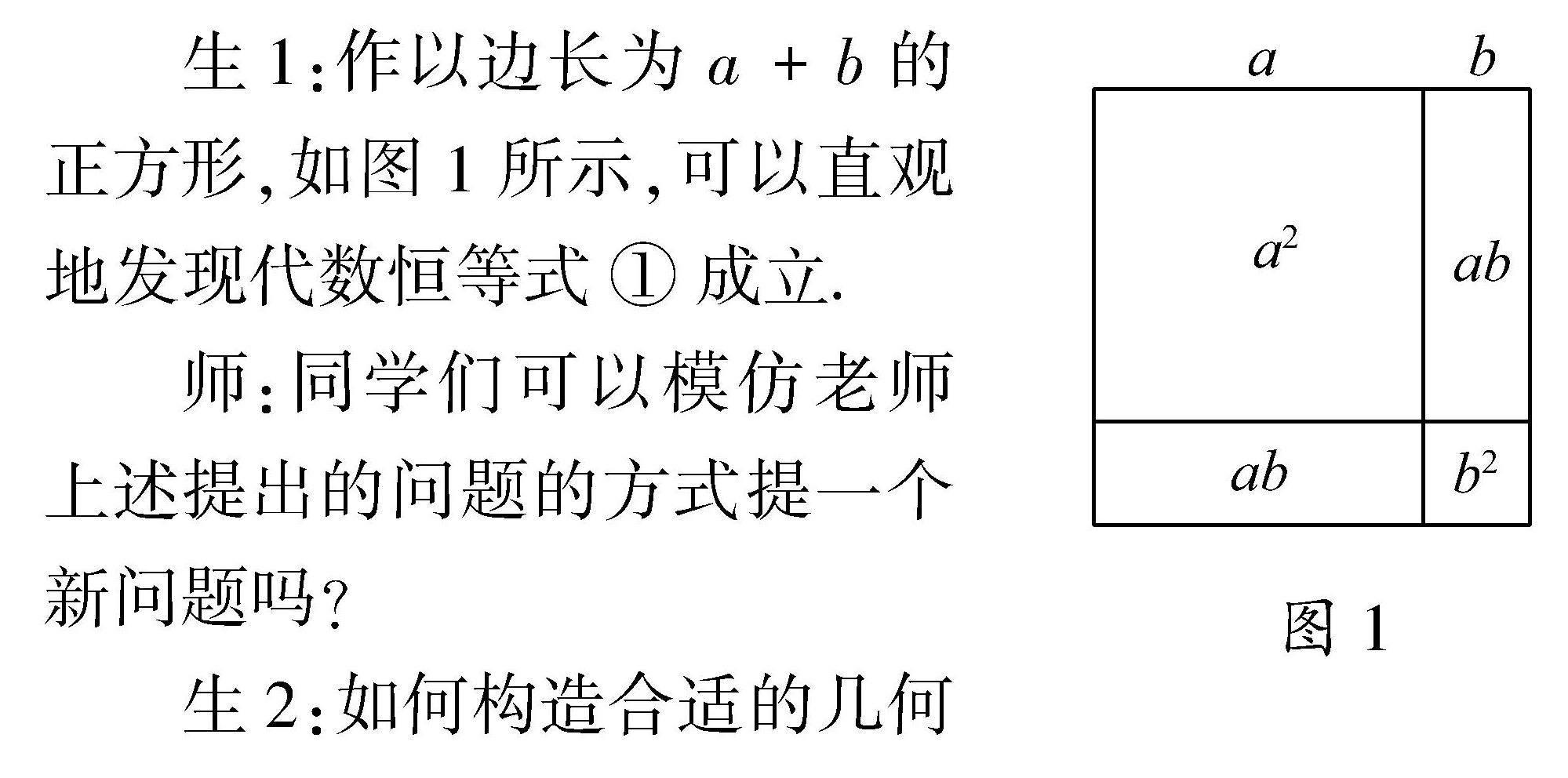
师：如何构造合适的几何图形检验两数和的完全平方公式（a＋b）2＝a2＋2ab＋b2①这一代数恒等式呢？

图1生1：作以边长为a+b的正方形，如图1所示，可以直观地发现代数恒等式①成立.

师：同学们可以模仿老师上述提出的问题的方式提一个新问题吗？

生2：如何构造合适的几何图形检验两数差的完全平方公式（a－b）2＝a2－2ab＋b2②这一代数恒等式呢？

师：好问题！大家如何解决这个问题呢？

生：……（省略号表示学生思维暂时中断）

师：大家发现无法使用验证代数恒等式①的方法验证代数证恒等式②成立.能否想出突破这种限制的方法呢？你可以提出一个新的问题吗？

生3：是否可以通过变形恒等式（a－b）2＝a2－2ab＋b2②获得一个新的恒等式的表达形式，从而有利于构造一个规则性的几何图形，使用其面积表达恒等式②呢？

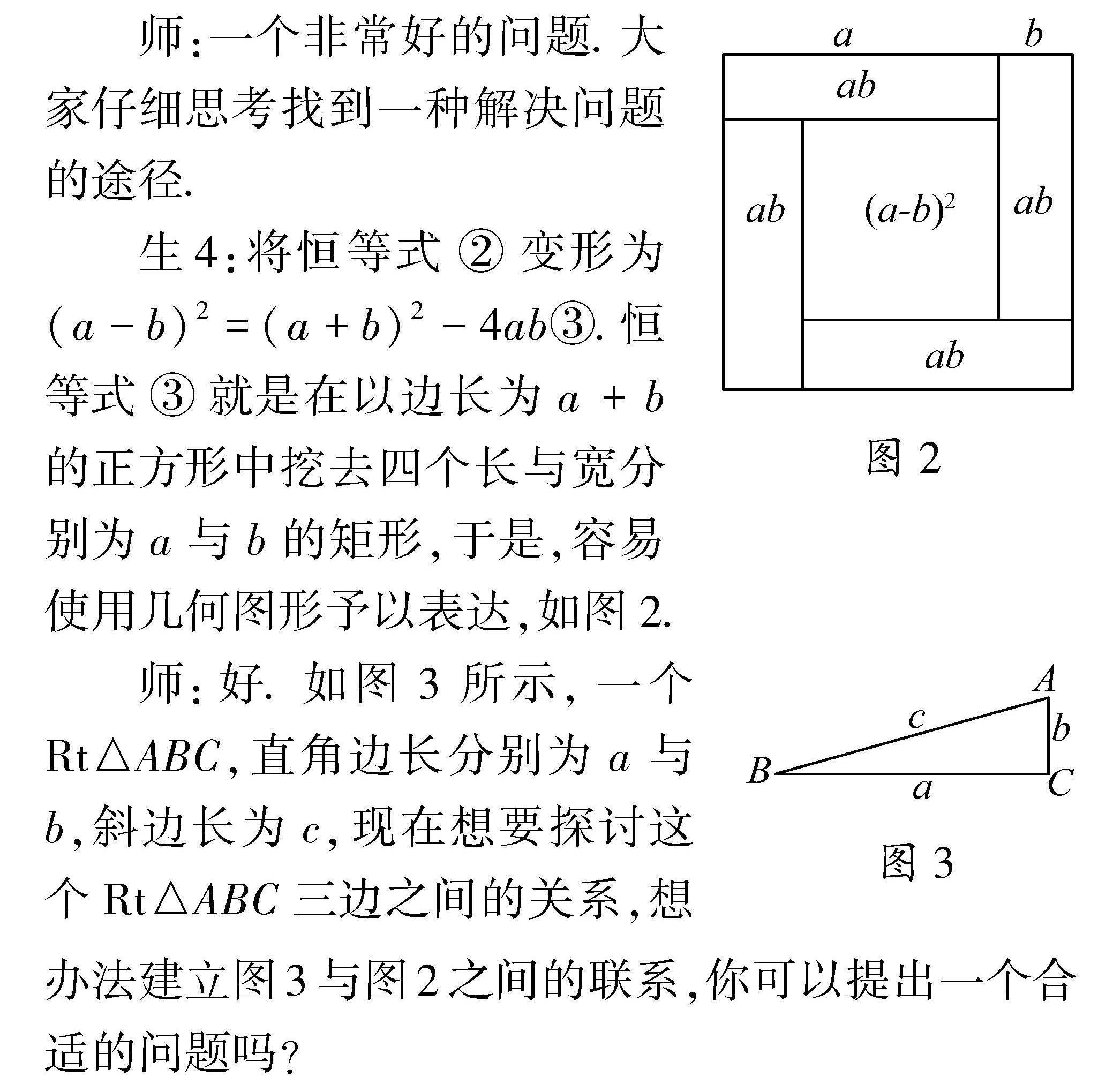
图2师：一个非常好的问题.大家仔细思考找到一种解决问题的途径.

生4：将恒等式②变形为（a－b）2＝（a＋b）2－4ab③.恒等式③就是在以边长为a＋b的正方形中挖去四个长与宽分别为a与b的矩形，于是，容易使用几何图形予以表达，如图2.

图3

师：好.如图3所示，一个Rt△ABC，直角边长分别为a与b，斜边长为c，现在想要探讨这个Rt△ABC三边之间的关系，想办法建立图3与图2之间的联系，你可以提出一个合适的问题吗？

生5：我看到了图2中存在着图3这样的直角三角形，只要作出图2中矩形的对角线，就能构造出图3的这个直角三角形了.如此，可以将图3放置到图2中去，作为图2的一个部分或一个元素.到此，我们提出这样的问题：当将图3放置到图2中去以后，可以利用图2中的几个直角边长分别为a与b、斜边长为c的直角三角形.现在想要利用图2来探究Rt△ABC三边之间的关系吗？

师：提出了很好的问题.如何利用图2来解决这个问题呢？

生6：图2中存在着四个矩形，这4个矩形可以分解成8个如图3这样的直角三角形，如果胡乱地连结这4个矩形的对角线，作出8个直角三角形，肯定不利于问题的解决……

师：分析得非常好.那么对此，大家可以提出怎样的一个新问题呢？

生7：如何连接图2中的4个矩形对角线，才有利于探讨Rt△ABC三边之间的关系呢？

图4生8：作出这4个矩形的对角线以后，使得这4条对角线所划分出的新图形一定是依据某种规则，从而有利于我们能够利用图形的整体性.如此，我想将图2划分为图4，即顺次连结图2中四个矩形的对角线，在图2中就构造出了8个所需要直角边长分别为a与b、斜边长为c的直角三角形.如图4，去掉图4中的相关线条，得图5，由图5容易知道（a＋b）2＝c2＋2ab，化简得a2+b2＝c2④.

师：好！直角三角形三边长的表达式④的形式，称为“勾股定理”.那么对于图4而言，还能提出其他问题吗？

生9：如果去掉图4中外围的四个直角三角形，就得到图6，图6是以边长为c的正方形，可知c2＝（a－b）2＋2ab，化简得c2＝a2＋b2［1］.  图5          图6

注  一般数学教师难以推敲出学生发生勾股定理认识的认知出发点是两数差的完全平方公式的几何面积的直观表示［2］.笔者认识到了这一点，基于此，在勾股定理知识的教学设计及课堂实施中，以两数和的平方公式的几何面积表示为初始问题，在以后疑难环节中，不断地启发学生提出合适数学问题，最终基于学生在各个环节上所提出的合适数学问题的解决，成功地发生勾股定理这个知识点认识.由此能够认识到，教师通过教材分析掌握具体数学知识点的来龙去脉具有怎样的重要意义，就启发学生提出合适的数学问题这方面来说，数学知识的结构性决定了数学知识点之间的联系是多么得重要.这种教学设计及课堂实施实践活动，充分体现了一惯性与连续性在培养学生提出合适数学问题能力中的作用.

2  在课堂实施中坚持差异性与适应性要求

学习主体所拥有智力的特点与人的脸面一样，千人千面，对于学习主体而言，学生感受外在信息造成的疑难，随着不同学生已经掌握了的知识、发生知识认识的体验及其形成经验、萌生的数学观念等的不同而不同，具有个性差异的心理特点，例如，某些信息因素的整合，对于甲可能是问题，对于乙就不是问题.因此，一方面，对于感受外在同样的信息，有的学生可能使用自己的知识与经验完全驾驭信息，不会感到疑难，而另一些学生可能就是难以迈过去的坎，构成了他们极大的疑难，在这种情况下，学生为了理解信息，发掘信息所可能形成的意义，就会提出一系列问题［3］.

另一方面，由于班级集体的作用，尽管不同学生基于自己的数学知识水平或经验层次，可能提出不同的问题，但是通过班级集体提出问题活动的交流，一个同学提出问题就会引起其他学生的评价或效仿，从而引起其他同学的思考，如此，如果前面同学提出的问题不够完善，那么后面同学在前面同学提出问题的基础上，就会思考修改已经提出了的问题，从而达到完善数学问题的目的.看笔者的一个解题教学实践中的真实例子.

师：9枚1圆面值的外观相同的硬币，其中有1枚是假的，已知假硬币比真硬币稍微轻一点，并且给你一架天平.从理解这些信息的内涵中，请大家提出一个问题.

生10：这个问题容易提出来，如何利用天平从这9枚硬币中辨别出这枚假硬币？（记为问题1）

生11：问题1不太好.我提出的问题是，最多可以使用几次天平才能辨别出这枚假硬币？（记为问题2）

生12：我以为问题1与问题2都不太好.我提出的问题是，最少可以使用几次天平才能辨别出这枚假硬币？（记为问题3）

注  这是对于学生在课堂上提出的问题进行评价后，再行提出的数学问题.

师：非常好.大家提出了这些各有价值的数学问题.现在要问：除了提出这三项问题以外，同学们还能够进一步提出一些问题吗？

生13：我提出的问题是，如何通过使用3次天平辨别出这枚假硬币呢？（记为问题4）

生14：我提出的问题是，如何通过使用2次天平辨别出这枚假硬币呢？（记为问题5）

师：非常好.我们如何解决问题5呢？（以下的教学活动这里就略而不记了）

注  （1）向学生提供外在对象性信息，然后启发学生自己阅读信息、分析信息、理解信息，从理解了的信息内容中提出具体的问题，这是启发学生提出数学问题教学设计的一种套路.由于学生的个性差异性，在理解信息时，逼近信息本质的层级不同，所提出的问题形式及其构成的解题任务与途径是不同的.然而无论如何，每个提出问题的同学，都会从中受到教益，即使有的同学在课堂教学现场上没有机会（如时间的限制）提出自己的问题，由于倾听自己的同学提出了不同的问题，也会进行评价与试图寻找方法解决问题从而受到教益.因此，这种启发学生提出问题的教学设计及课堂实施是一种很好的途径.

（2）在学生提出这些问题后，数学教师可以在课堂上比较这些问题之间的区别与联系，然后依据学生解决数学问题的思维水平、意识观念、方法技巧等，选择其中具有典型意义的问题，引导学生探究解题方法，从而发挥学生提出问题所形成的问题组的作用.这种通过鼓励学生提出合适数学问题的课堂生成内容及其同学之间的交流，具有非常好的教学价值.

3  在课堂实施中坚持期待性与鼓励性要求

在启发学生提出合适数学问题的教学设计及课堂实施中，教师的期待具有很好的作用.期待是一种情感效应.期待意味着教师充分信任学生关于某项学习内容的学习潜力，相信学生通过自己的独立学习活动，在不久的将来会生成良好的学习结果.数学教师在以启发学生提出数学问题为目标进行教学设计及课堂实施时，向学生展示具体的数学信息，要求理解信息意义并从中提出问题，大多数情况下，学生不可能一蹴而就，他们必须要经由思考、实验、探究与选择，才能提出某些数学问题，这就必须要有充足的学习活动时间作保证.教师的期待就是应该提供给学生合适的时间，而不能急迫地要求学生立即作出回答.

例如，在施教勾股定理这个知识点的上述教学过程中，对于生3所提出的这个问题，笔者在课堂上足足地等待了4分钟.在这种等待的过程中，笔者始终微笑着注视学生，从学生的动作、表情与眼神中，切体地感受到了学生那种鸦雀无声的沉默（这是最令教师欣赏的课堂上的沉默），每一名进入角色的学生正是在这种沉默中，心智的思维活动在高速度地运转着，笔者十分把握地认为，学生肯定会提出突破探究思路活动困难的有启发性的问题.果不其然，学生做到了，这是笔者心理上的最大快慰之处.如果数学教师失去了期待的耐心，则会中断学生的思考，而将教师自己在备课中已经整理好了的思维活动结果奉献于学生，那就极大损失了启发与引导的教学价值.

对于数学教师来说，一方面，期待与鼓励是交织在一起的，期待本身就是一种鼓励，因为学生可以感受到教师的期待，就是相信学生通过自己分析信息，进行思考，一定可以获得有价值问题或结果；另一方面，当学生提出有分量的合适数学问题时，教师应该在课堂上热情洋溢地提出表扬，这是一种直接鼓励，即使学生提出的问题存在瑕疵，不太合适，应该基于学生回答的内容，需要充分肯定其价值所在，实事求是地进行分析评价，提出希望在那一点上作出了改正以后，就是一个合适的数学问题.总之，教师的期待与鼓励对于弘扬主体精神，激发学生独立学习具有重要作用.

4  结束语

在教学设计及课堂实施时，引导学生提出合适数学问题的主导责任在数学教师，教师需要自觉自愿地发挥自己在数学教学中的主导作用，首先应该发展自己面临外在信息时提出合适数学问题的能力，基于自己提出合适数学问题的经验，在教材分析时，洞穿所要施教的数学知识点的本质，从中发现与选择具体数学知识点作为学生发生数学知识点认识的认知出发点［4］.在具体数学知识点的教学设计及课堂实施时，数学教师需要依据一惯性与连续性、差异性与适应性、期待性与鼓励性三项要求展开课堂活动.

参考文献

［1］张昆，曹一鸣.完善数学教师教学行为的实现途径［J］.数学教育学报，2015，24（01）：33-37.

［2］张昆.教材分析：数学教学设计的基础［J］.中学数学杂志，2018（08）：13-16.

［3］张昆.学情分析：数学教学设计的前提［J］.中学数学杂志，2017（12）：5-8.

［4］张昆.增进学生理解弘扬主体精神：数学教学设计从逻辑分析转向心理分析的视点［J］.中学数学教学，2017（05）：4.

作者简介  张昆（1965—），男，安徽合肥人，中学高级教师，副教授，博士，师从北京师范大学曹一鸣教授、陕西师范大学罗增儒教授和浙江师范大学张维忠教授;主要研究数学解题教学、数学教学设计、数学史、中小学数学教师培训等；发表数学教育教学论文300余篇，其中28篇被人大复印资料全文收录.