多位数乘法与多项式乘法之间的迁移联系
牛延凯 李倩


【摘 要】 中学阶段,数学学习的一个重要转变是从数到式的抽象,并从数的运算过渡到式的运算.具体到乘法运算,整数乘法看作是整式乘法的算术形式,而整式乘法蕴含了整数乘法所遵循的代数原理.教学中可以通过运算结构的迁移、算理的迁移、算法的迁移三个角度把握整数乘法与整式乘法之间的迁移联系,进而把整数乘法中的多元计算方法与技巧迁移到整式乘法中,提高多项式乘法运算效率,实现算术运算到代数运算的过渡.
【关键词】 多位数乘法;多项式乘法;学习迁移;知识联系
从小学到中学,数学学习的一个重要任务是完成从数到式的抽象,并进一步由数的运算迁移到式的运算.从数的加减到整式加减、从整数乘法到整式乘法、从分数运算到分式运算,数和式的运算过程在一定程度上具有相似的本质属性,数的运算可以看作式中字母取某些值的特定结果,而式的运算则超越了数的具体束缚,其过程更加形式化和抽象化,更能揭示运算的一般性规律.
多位数乘法是小学整数乘法中的难点,而多项式乘法是中学整式乘法中的难点,两者在运算结构、算理、算法上存在密切联系.布鲁纳认为,在没有相互关联的结构基础上进行灌输教学是“不经济的”,所获得的知识非常容易遗忘.因此建立整数乘法与整式乘法之间的迁移联系,可在相互关联的结构中帮助中学生充分利用多年来积累的乘法算术经验,提升多项式乘法的学习效率,并进一步实现算术运算到代数运算的过渡.
1 运算结构的迁移:多位数乘法中体现了多项式乘法的运算结构
1.1 多位数乘法的常见算法
人教版教材以14×12为例,开始学习最基本的多位数乘法——两位数乘两位数.除了竖式乘法外,多个版本教材中也介绍了乘法计算的不同方式,这里呈现三种不同的算法计算14×12.
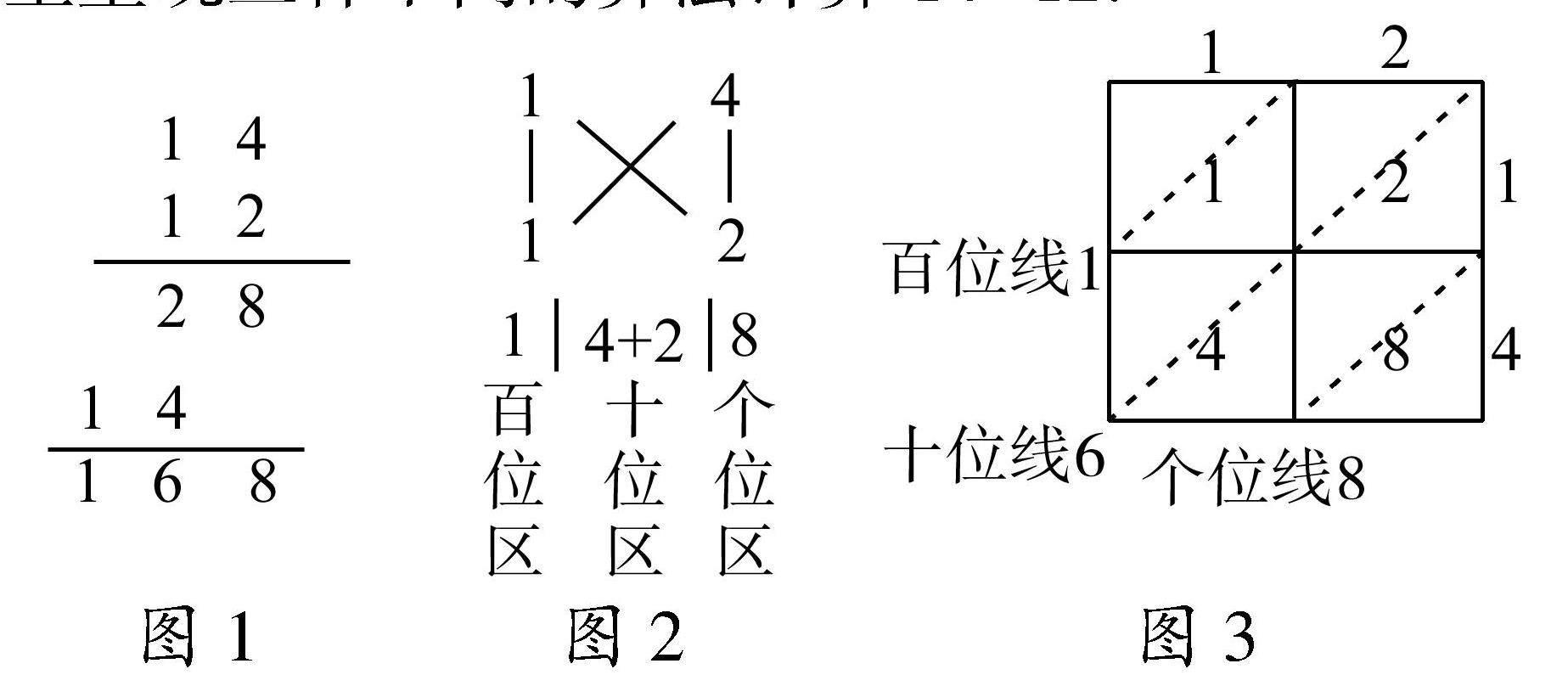
图1 图2 图3竖式乘法 十字相乘法 格子乘法不进位形式
(1)竖式乘法.如图1,学生最为熟悉的计算方式,分为三步,逐位相乘,先算14×2的积,再算14×10的积,最后相加.
(2)十字相乘法.如图2,分为三步,两个因数的个位数字相乘,得出积的个位数字;中间交叉相乘后,把结果相加得积的十位数字(2×1+1×4=6);两个因数的十位数字相乘,得积的百位数字.这个过程中由逐位相乘转为对位相乘,也叫十字相乘法[1].
(3)格子乘法(铺地锦).我国明朝的《算法统宗》讲述了一种“铺地锦”的乘法计算方法,是利用格子来算的[2].格子乘法中,需把每个小方格一分为二,便于记录每次相乘后的进位数字.由于14×12是不进位乘法,可简化小方格的分割过程,写成一种运算表形式,如图3,14沿纵轴排列,12沿横轴排列,每个方格内记录各位数对应相乘的积,从右下角开始作个位数,沿倾斜方向把每条对角线的数相加,分别得出积的十位数字和百位数字.
1.2 三种算法的共通性——体现了多项式乘法的运算结构
虽然三种算法规则差异较多,但基本结构是相似的.可以发现,14×12的计算过程都分解为4个基本算式:①2个一×4个一=8个一;②2个一×1个十=2个十;③1个十×4个一=4个十;④1个十×1个十=1个百.
①式2×4,个位数字×个位数字,结果是若干个一,因此8写在积的个位区;②式2×1和③式1×4,都属于个位数字与十位数字相乘,结果是若干个十,2个十+4个十=6个十,因此6写在积的十位区;④式1×1,十位数字×十位数字,结果是若干个百,因此1写在积的百位区.
以上算式中的数字赋上计数单位,得14×12=2×4+2×10+10×4+10×10,即(10+4)×(10+2)=2×4+2×10+10×4+10×10,转换为字母表示为(a+b)×(c+d)=
d×b+d×a+c×b+c×a.
可以发现,多位数乘法中渗透了多项式乘法法则,多位数乘法遵循多项式乘法的运算结构,从多位数乘法到多项式乘法,是一种从数到式、从特殊到一般的迁移.
2 算理的迁移:多位数乘法与多项式乘法的算理一致性
2.1 算理的一致性:借助乘法分配律化繁为简
鲁宾斯坦指出,通过概括把握两种学习间的一般原理和本质规律,能产生更广泛的迁移,他认为必须找到一般原理、整理出知识结构、概括出一类事物的本质规律,才能对课题类化,进而解决问题[3].迁移的关键在于概括两个对应模块之间的共同原理和思想方法,而纵观多位数乘法和多项式乘法的学习过程,转化思想和乘法分配律的应用贯穿始终,即借助乘法分配律不断的把乘法运算化繁为简.
(1)整数乘法中,多位数乘一位数时,如图4,其竖式算理用横式形式展开为:12×3=3×2+3×10,即借助乘法分配律把多位数乘一位数转化为一位数乘一位数(3×10本质上借助乘法口诀3×1计算).后续在多位数乘多位数时,如图1,先是借助乘法分配律先转化为多位数乘一位数,14×12=14×2+14×10,最后再次借助乘法分配律转化为4个一位数乘一位数的基本算式.
图4 人教版两位数乘一位数例题
(2)同理,整式乘法中,多项式乘单项式时可借助乘法分配率转化为单项式乘单项式,如(a+b)×c=a×c+b×c;后续,多项式乘多项式时仍是借助乘法分配率先转化为多项式乘单项式,再转化为单项式乘单项式,如:
(a+b)×(c+d)=(a+b)×c+(a+b)×d=a×c+b×c+a×d+b×d.
因此,无论是多位数乘法还是多项式乘法其算理核心都是在转化,不断的把复杂运算转化为基本运算:把多位数乘法最终转化为一位数乘一位数,把多项式乘法最终转化为单项式乘单项式,而乘法分配律是支撑这一转化过程的核心定律.
2.2 一致性的背后
从多位数乘法到多项式乘法体现了从特殊到一般的迁移规律,可进一步解释其深层原因.由于整数乘法采用十进制计数法,因此14×12=168可用10的乘方形式展开:(1×10+4)×(1×10+2)=(1×102+6×10+8).用字母代替进制10,可抽象为一般情况,(x+4)×(x+2)=(x2+6x+8).因此,从运算进制角度看,多位数乘法可以看作多项式乘法在算术进制为十时的特殊形式,两者在计算结构、算理上可以形成从特殊到一般的迁移联系.
3 算法的迁移:多位数乘法的运算方式与技巧应用于多项式乘法
在运算结构迁移和算理迁移的基础上,算法层面,整数乘法中的竖式乘法、十字相乘法、格子乘法等诸多计算方式和计算技巧也可迁移用于多项式乘法,丰富多项式乘法的学习路径,提升运算效率.
3.1 竖式乘法应用于多项式乘法
教材中多项式乘法主要是横式形式,如(x+4)×(x+2)=x2+2x+4x+2×4,而整数乘法常用的竖式计算方式在适当处理后可迁移到多项式乘法中.
(1)不发生进位时,多位数乘法与多项式乘法的竖式结构类比.
以(x+4)×(x+2)为例,可以运用竖式形式计算,其算法结构与14×12的竖式过程可以对应联系:
图5
(2)有进位时,多位数乘法与多项式乘法的竖式结构类比.
以(3x2+x+2)×(x2+3x+4)为例,也可以用竖式形式运算,其算法结构与312×134发生进位前的竖式过程可以对应联系:
图6
结合以上过程,可发现多项式乘法与多位数乘法在竖式结构中的对应关系:个位区对应常数项,十位区对应一次项系数,百位区对应二次项系数,以此类推,可以把多项式乘法转化为进位前的多位数乘法形式.由于多项式中非同类项系数之间不能合并,与其对应的整数乘法各数位区之间不发生进位即可.
3.2 格子乘法(不进位形式)应用于多项式乘法
(1)格子乘法(不进位形式)用于计算多项式乘法.
多项式乘法非同类项系数之间不产生进位,因此格子乘法计算多项式乘法时,只需借助其不进位形式.如(x2+x+2)×(2x2+3x+2):
图7
根据多项式乘法和多位数乘法的对应关系,万位线对应4次项系数,千位线对应3次项系数,百位线对应2次项系数,十位线对应1次项系数,个位线对应常数项,得(x2+x+2)×(2x2+3x+2)的结果为2x4+5x3+9x2+8x+4.
(2)格子乘法用于直观理解多项式乘法的计算公式.
相比较横式、竖式等乘法形式,格子乘法中的矩阵形式更具有直观性,有助于各种乘法公式的直观理解和快速记忆.如下:
图8 用格子乘法直观理解各种乘法公式
这里的格子乘法(运算表)虽然在形式上类似于面积图法,但其本质上是一种矩阵形式,其优势在于数的大小和正负性不需要和线段长短建立对应关系,应用时局限性更小.
3.3 十字相乘法应用于多项式乘法
(1)十字相乘法用于计算二项式乘法.
整数中的十字相乘法可以迁移到中学,用于快速计算二项式乘法.如(x+4)×(x+2)可以类比14×12的计算过程,用十字相乘法展开:
图9
(2)十字相乘法用于理解多项式乘法的逆运算——因式分解.
理解的程度信赖于新知识与认知结构之间联系的多与少、强与弱[4],而由于学生原有的乘法经验中缺少十字相乘法,所以在学习十字相乘法分解因式时,学生往往知其然,不知其所以然.
图10ax2+bx+c中,如果二次项系数a=a1×a2,常数项c=c1×c2,而a1c2+a2c1恰等于一次项系数b,则有ax2+bx+c=(a1x+c1)×(a2x+c2),这种因式分解的方法称为十字相乘法,如图10.
其中,左侧相乘等于二次项系数,右侧相乘等于常数项,中间交叉相乘再相加可得一次项系数.追根溯源后,学生会发现这个过程和之前整数(整式)乘法中的十字相乘计算方式是一种互逆关系,进而在其基础上理解十字相乘法因式分解的原理以及产生源头:既然十字相乘法可以用于整数乘法、整式乘法,也当然能用于整式乘法的逆运算——因式分解.
3.4 综合运用竖式乘法、格子乘法、十字相乘计算多项式乘法
以(5a+2b)×(3a+b)为例,除了基本的横式计算,可迁移运用整数乘法中竖式乘法、格子乘法、十字相乘法等,实现算法多样性和运算高效性,如下:
图11
显然,以上多种计算方式都可得出(5a+2b)×(3a+b)=15a2+11ab+2b2.
算术教学中可由过程性观点向结构性观点做必要转变,代数即概括[4].整体把握数到式的迁移学习过程,可以从算术运算中概括其代数结构和本质算理.从这个角度,多位数乘法看作是多项式乘法的算术形式,而多项式乘法蕴含了多位数乘法背后所遵循的代数原理,建立两者之间的关联结构,有助于实现算术思维和代数思维的过渡,而学生长期积累的算术经验和方法技巧也可以有效迁移到代数学习中,进而降低代数运算难度.
参考文献
[1]王丽娜.两位数相乘的简捷算法[J].珠算与珠心算,2017(04):22-24.
[2]刘令,徐文彬.我国小学数学教科书中数学史料的分析与批判[J].全球教育展望,2008(07):87-91.
[3]杨俊林.例谈灵活解决数学问题的心理机制及教学对策[J].中国数学教育,2012(20):10-12,14.
[4]郑毓信.算术与代数的区别与联系[J].小学教学研究,2011(19):11-14.
作者简介 牛延凯(1987—),男,山东淄博人,中学一级教师,淄博市教学能手;多次主持和参与省市级课题;主要研究中小学数学的核心知识与结构化教学,发表论文10余篇.
李倩(1985—),女,山东淄博人,中学一级教师,淄博高新区教学能手、教学工作先进个人;多次参与省市级课题研究;主要研究数学教学与评价.

