将中华优秀传统文化融入跨学科项目化学习的设计与思考

严艳 潘小明

基金项目  江苏省中小学教学研究第十四期重点资助课题“初中数学跨学科综合实践的资源整合与项目设计”（2021JY14-ZA09）.

【摘  要】  将中华优秀传统文化融入初中数学跨学科项目化学习是提高学生综合人文素养的重要手段之一.文章以“让制作的杆秤称重范围更大”的设计为例，阐述了利用跨学科项目化学习，发展学科与跨学科核心素养，引导学生在合作探究中主动学习中华优秀传统文化知识，建立文化自信，落实立德树人.

【关键词】  中华优秀传统文化；跨学科学习；项目化学习

《义务教育数学课程标准（2022版）》（以下简称新课标）在课程内容选择中指出“要关注数学文化，继承和弘扬中华优秀传统文化”，在教材编写建议中强调要“展现数学发展史中伟大数学家，以及他们的数学成果在人类文明发展中的作用，增强学生的爱国情怀和民族自豪感”［1］.我国的传统文化源远流长，博大精深，凝聚了华夏先哲们无穷的智慧，在数学学科教学中传承和发扬中华优秀传统文化不仅重要、必要，而且具有非常深远的历史意义，这并非是简单的、注入式的知识讲授，而是结合相关主题在跨学科项目化数学活动中进行数学方法的引导、数学思想的启迪和与此相关传统文化的渗透、融入.本文以“让制作的杆秤称重范围更大”的设计为例，初步探讨初中数学教学如何继承和弘扬中华优秀传统文化.

1  中华优秀传统文化与跨学科项目化学习

1.1  中华优秀传统文化的教育意义

习近平总书记指出：“中华优秀传统文化是中华民族的‘根和‘魂，是最深厚的文化软实力，是中华特色社会主义植根的文化沃土，是我们在世界文化激荡中站稳脚跟的根基.”［2］从教育的角度来分析，中华优秀传统文化不仅可以滋润人们的心灵，启迪人们的心智，而且可以为学生持续、深入的学习提供丰厚的文化滋养，为学生积极、健康的发展提供强大的精神支撑.就数学教育而言，应通过有效的教学，让学生体验古代先贤的智慧、感悟中华优秀传统文化的博大精深、增强爱国情怀和民族自豪感，坚定落实立德树人的根本任务.

1.2  将中华优秀传统文化融入跨学科项目化学习

跨学科项目化学习强调在解决真实、复杂的问题中学习、运用不同学科的知识，强调通过学习产生具有整合性的成果与理解［3］.将中华优秀传统文化有效融入跨学科项目化学习，不仅可以创新中华优秀传统文化继承、弘扬的路径，而且可以充实数学文化渗透、优化数学活动学习的资源.深挖中华优秀传统文化中的数学教学资源，以跨学科项目化学习为载体，可以引导学生在数学知识探究、获取的过程中积累数学活动经验、拓展数学思想方法、优化数学思维品质、提高人文素养，促进学生数学素养和精神境界的双升华.为了让学生感悟中华优秀传统文化中所蕴含的多个学科核心知识和能力，发展跨学科核心素养，数学教师需要深度挖掘数学教学内容的文化内涵，将学习内容设计成可以实施的“项目”，利用学科及跨学科的综合知识促进学生数学知识的深度融合，经历解决真实问题的过程，并因此形成整合性的项目化学习成果和更有深度的数学知识理解.

2  将中华优秀传统文化融入初中数学跨学科项目化学习的设计

“让制作的杆秤称重范围更大”的项目建立在学生对杆秤已有初步的感性认识，通过数学及跨学科知识进一步研究称重原理等问题，从而上升到理性思维的活动项目.这个项目蕴含初中数学一次函数的相关内容，用一次函数知识理解并解释杆秤的刻度均匀，运用跨学科物理中的杠杆原理建立方程，灵活运用方程模型扩大量程.学生在此项目活动中对杆秤的文化内涵有了更深刻的理解，一方面，是对以墨子为代表的古代先贤的敬仰，另一方面也感受到古人对商业诚信的追求.

为了让学生更充分的进行项目研究，设计以下5个大环节，如图1.

时间为课上课后相结合，其中了解结构、研析原理、设计方案、阶段交流、成果展示课上进行，3课时左右；查阅资料、实物研究、制作校验、优化量程、评价反思课后进行.

2.1  创设中华优秀传统文化情境，启动项目

问题情境  杆秤是华夏“国粹”，具有悠久的历史.它制作轻巧、经典，使用也极为便利，作为商品流通的主要度量工具，活跃在大江南北，代代相传.天地间有杆秤，人们不断赋予秤的文化内涵，公平公正的象征，天地良心的标尺，一桩桩交易就在秤砣与秤盘的此起彼伏间完成.部分同学在小学里已尝试做简易小杆秤，利用它可以称出一些物体的重量，如何在保持秤杆、秤盘（秤钩）和秤锤不变的基础上，使它的称重范围更大？为了解决这个问题，你想从哪几个方面展开研究呢？

2.2  挖掘中华优秀传统文化内涵，学科融合

预设任务（1）：杆秤的构造和发展史.

杆秤是在天平的基础上发展而来，是中华两千多年封建经济中最基本的测重工具，由木制的带有秤星的秤杆、秤锤和提纽等组成.古代定秤，以天上的星星为依据，北斗七星、南斗六星、福禄寿三星共十六星，所以古代一斤为十六两，半斤即是八两，少一两叫“损福”，少二两叫“伤禄”，少三两叫“折寿”.称重时，当杆秤保持水平平衡，就可根据秤锤的位置读出物体质量.

预设任务（2）：确定杆秤的零刻度（定盘星）.

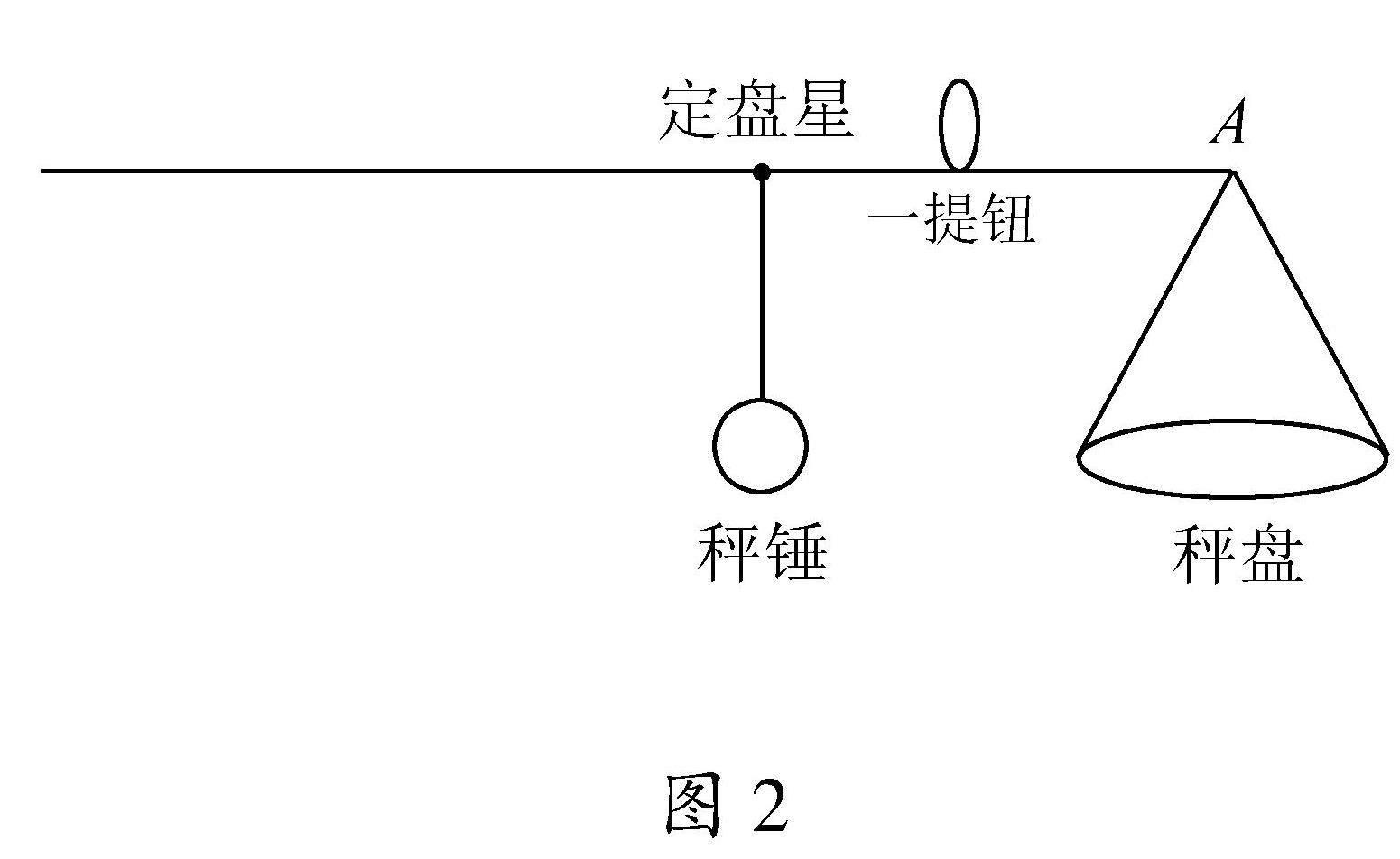
当秤盘中不放任何物体时，移动秤锤至秤杆保持水平平衡，此时秤锤的位置即为“定盘星”的位置，相当于杆秤的零刻度，如图2.

预设任务（3）：杆秤的刻度是否均匀.

研究方法：采用物理中常用的控制变量法，通过实验收集数据，借助技术分析数据，运用演绎推理说明数据.

数学实验：

（1）实验收集数据：固定图中秤盘、秤锤的重量，以及定盘星和一提钮到点A的距离，杆秤称重水平平衡时，测量物体的重量x以及秤锤到定盘星的距离y，列表整理数据；

（2）技术拟合图像：把实验收集的数据按照（x，y）顺序输入图形计算器，呈现散点图，利用工具拟合图像，得到一次函数的关系式，通过一次函数说明杆秤的刻度是均匀的.

杆秤的工作原理：物理中的杠杆原理，亦称“杠杆平衡条件”，最早由古希腊学者阿基米德在《论平面图形的平衡》一书中提出，即“二重物平衡时，它们离支点的距离与重量成反比.”通俗讲就是“动力×动力臂=阻力×阻力臂”.实际上，早在公元前4—3世纪，《墨经》中对衡器和杠杆原理已作了精辟的论述，“横，加重于其一旁必捶，权重相若也，相衡，则本短标长，两加焉，重相若，则标必下，标得权也”.这段文字讲的是天平横梁的一臂加重物，另一臂必得加砝码，两者必须等重，才能平衡；杆秤的提纽到重物的一臂比较短，提纽到秤锤的臂比较长，如果两边等重，秤锤一边必下落.《墨经》中对平衡原理的阐述比阿基米德早了近200年.

演绎推理：如图3，设秤盘吊绳处A至一提钮和定盘星（O点）的距离分别为a1和a，秤锤重为G，秤盘重为G0.根据杠杆原理可得G（a－a1）=G0a1.①如图4，把重x的物体放入秤盘中，提起一提钮，移动秤锤至距离点O为y处杆秤保持平衡.根据杠杆原理可得G（y+a－a1）=（G0+x）a1.②由①②两式可得y=a1Gx.其中，a1，G为常量，则y是x的一次函数，因此，杆秤的刻度是均匀的.

2.3  凸显文化承载的理性思维，扩大量程

预设任务（4）：扩大杆秤的称重范围.

预设问题：

（1）杆秤实物上的两个提钮，是怎么回事呢？

通过观察和实践，发现杆秤上离秤盘吊绳处A较近的提钮（二提钮），可以称出更大的重量，原因是根据杠杆原理，在力矩不变的前提下，减小力臂，可以增大力.通过增加“提纽”可以扩大称重范围.

（2）二提钮的位置如何确定呢？

二提纽的最小称重量为一提纽的最大称重量，若所做杆秤的秤锤离点O最远距离为l，则一提钮的最大称重量G1=Ga1l.如图5，设二提钮到A点距离为a2.根据杠杆原理

G（a－a2）=（G0+G1）a2.③则a2=GG+G0+G1a.即可确定二提钮的位置.

（3）利用二提钮如何称重？

如图6，把重x（x>G1）的物体放入秤盘中，提起二提钮，移动秤锤至距离点O为y处，杆秤保持平衡.根据杠杆原理可得G（y+a－a2）=（G0+x）a2.④由③④两式可得a2x－Gy=G1a2.其中，a2，G，G1为常量，则y仍是x的一次函数，因此，使用二提钮称重杆秤的刻度同样是均匀的.称重读数利用x=Ga2y+G1读出.图6

预设任务（5）：杆秤的制作和校验.

预设问题：杆秤称重的准确性与哪些因素有关呢？

称重结果是否准确，还跟秤杆、秤盘（秤钩）和秤锤的重量有关联.为了减少误差，秤杆的自重尽量要轻，秤盘（秤钩）和秤锤的重量要精准，为了便于读数，秤盘（秤钩）和秤锤的重量尽可能为整数.

2.4  呈现跨学科项目学习成果，展示交流

展示要求：各小组代表用制作的杆秤现场称重，展示其精确度和称重范围.

交流要求：在制定方案或制作杆秤的过程中发现、提出的问题，以及在课后分析、解决的方法与同学们分享.

评价要求：根据评价方案（表1）作相应点评.

3  将中华优秀传统文化融入初中数学跨学科项目化学习设计的思考

立德树人是各个学科教育教学的根本任务.较之于其他学科的教育教学，数学学科因其抽象性、严谨性而加强了学生理性思维的培养，弱化了数学文化对于立德树人的价值.中华优秀传统文化是数学思政渗透的优质资源.将中华优秀传统文化融入初中数学跨学科项目化学习，可以激活蕴含于数学教育教学内容中类型多样、思维深刻和内涵丰富的数学文化，可以实现中华优秀传统文化、数学文化立体化育人的同频共振与同向同行.在当前倡导学生核心素养培养的新时代背景下，应当重视数学教学内容背后中华优秀传统文化的挖掘，经由数学跨学科项目化学习融入中华优秀传统文化，继承和弘扬中华优秀传统文化，将学生的数学自信与文化自信相互贯通.为了实现这样的目的，在数学教学设计中不仅要注意挖掘项目活动中中华优秀传统文化内涵的多元性，而且要注意强化学生在驱动性问题解决活动中的主体思维，通过跨学科项目化学习的成果展示、知识分享和文化交流要突出数学学习中过程与结果的并重.

3.1  挖掘项目活动中中华优秀传统文化内涵的多元性

“让制作的杆秤称重范围更大”的项目基于中华优秀传统文化，从问题情境、资料搜集、设计方案、制作校验、成果汇报等各个环节中都展现其内涵的多元性，体现如下：

（1）思想性.通过对杆秤文化深入了解，学生感受到中华优秀传统文化的博大精深，体会到古人对诚信的追求，增强了爱国情怀和民族自豪感；同时，在杆秤发展史中起着不可磨灭作用的《墨经》对后世的影响不仅仅展示了当时先进的科学技术，还有墨子提出的著名的三种学习途径，“亲知闻知说知”，尤其以“说知”为其特色，以逻辑为推导手段作为获取知识的方法，体现了学习过程中理性思维的重要性.

（2）跨学科性.“让制作的杆秤称重范围更大”的项目融合数学和物理等学科知识，根据物理中控制变量法厘清研究对象，运用跨学科思维理解称重原理；从数学学科角度理解，利用杠杆原理建立模型，运用数学一次函数的知识分析、解释杆秤制作中刻度标记以及较为复杂的增加二提钮扩大量程的问题.

（3）趣味性.中华优秀传统文化中积累了丰富且有趣的学习素材，如古代发明、建筑、生活器物等，凝聚了古代匠人的巧思和智慧，能激发学生的学习兴趣；项目化活动的特点促使学生通过合作探究、动手实践的方式去解决具有挑战性的问题，必然会增加学生探索的乐趣.

3.2  强化学生在驱动性问题解决活动中的主体思维

将中华优秀传统文化融入初中数学跨学科项目化学习设计并不是追求一时的时髦，也不是吸人眼球的花俏，而是瞄准学生核心素养培养、驱动性问题解决、数学活动推进、高阶思维训练等目标，思考如何落实跨学科项目化学习中数学文化与中华优秀传统文化互融式教学的创新设计.由此，驱动性的问题解决和学生主体的数学思维显然不仅是教学的前提，而且是教学设计得到有效实施的关键.教学实践表明，为了解决真实情境中非良构问题，不仅需要对驱动性问题提出若干子问题进一步研究，而且要对学生在驱动性问题解决活动中的主体思维进行教学设计研究，要分析“如何从数学的角度去发现并提出问题”“如何发展学生会用数学的眼光观察现实世界”.作为有效的教学策略，解决驱动性问题的若干子问题可以由学生主动提出，教师在设计项目时，需要合理预设学生可能提出的问题，并在项目实施时及时做出调整或指导，以学生为主体，帮助学生架构项目学习的框架.

3.3  突出跨学科项目化学习过程与结果的并重性

学科项目学习应该具有鲜明的学科特色，数学是以思维活动为主的学科，其成果理应以“思维产品”（体现过程导向）为主，追求成果的代数表达（体现结果导向）［4］.因此，将中华优秀传统文化融入初中数学跨学科项目化学习，不仅要重视学习成果的展示，而且要重视学习过程的优化.小组代表在展示杆秤称重及交流过程时，不一定面面俱到，可以选择制作过程中如何发现并提出问题，又是如何解决的过程进行交流.如观察到杆秤上有两个提钮，发现较轻和较重的两个物体称重时使用了不同的提钮，这两个提钮各自的称重范围是多少呢？这是学生直观感受和经验驱使所发现并提出的问题，把这个问题通过跨学科思维理解分析并数学化的过程即为问题解决的过程.

参考文献

［1］中华人民共和国教育部.义务教育数学课程标准：2022年版［M］.北京：北京师范大学出版社，2022：89-90.

［2］中共中央宣传部.习近平新时代中华特色社会主义思想三十讲［M］.北京：学习出版社，2018：206.

［3］夏雪梅.跨学科项目化学习：内涵、设计逻辑与实践原型［J］．课程·教材·教法，2022（10）：78-84．

［4］王红权.项目学习：初中数学跨学科综合实践的主要方式［J］．中华数学教育，2022（09）：10-14．

作者简介  严艳（1978—），女，中学高级教师;主要从事课例研究、命题研究.

潘小明（1969—），男，博士，三级教授，硕士生导师;主要从事基础数学、数学教育、教师教育和教育管理等研究.