基于操作体验 发展空间观念

宾旋

［摘 要］文章通过对人民教育出版社根据2001年版课标编写的实验教科书（以下简称“实验版教材”）和根据2011年版课标修订的义务教育教科书（以下简称“修订版教材”）中“图形的旋转”这部分内容进行纵向对比分析，并结合学情分析，寻找基于操作体验，发展空间观念素养，帮助学生感悟旋转本质特征的教学启示。

［关键词］空间观念；操作体验；图形的旋转

［中图分类号］ G623.5［文献标识码］ A［文章编号］ 1007-9068（2024）14-0050-04

《义务教育数学课程标准（2022年版）》指出，空间观念是核心素养的主要表现之一。主要是指对空间物体或图形的形状、大小及位置关系的认识。

一、教材分析和学情分析

（一）教材分析

“图形的旋转”是在学生二年级初步认识了生活中的旋转现象后学习的。本节教学内容主要是进一步认识图形的旋转，探索旋转的特性，并要求学生能在方格纸上画出简单图形旋转90°后的图形，能从旋转的角度欣赏生活中的图形，进一步感受图形变化带来的美。教学过程中，教师应善于利用学生的原有认知推动新知的学习，并注意新旧知识的衔接。

1.引入部分的对比

实验版教材直接提问：“你见过哪些旋转现象？”而修订版教材通过呈现风车、钟面等素材，唤醒学生的旋转经验。相比之下，修订版教材更直观。

2.构建旋转概念的对比

两个版本的教材有相同的地方，也有不同的地方。相同点：二者都是以钟面指针的旋转为素材来引出旋转的三要素。不同点：描述旋转过程的方式不同。实验版教材是按旋转的起点到过程再到终点的方式描述；修订版教材增加了“方向”这个词，明确从几到几，指针绕点O按什么方向旋转了几度。先明确旋转的前后位置，再描述旋转的过程，更符合学生的思维顺序。

3.感受旋转特性的对比

两个版本的教材都是按照先观察，再对比旋转前后位置的变化，最后归纳总结旋转的特性这样三个步骤来编排的。修订版教材进行了以下四项改进：第一，实物模型由风车更换为三角尺，使学生观察的对象更为明确，减少干扰；第二，旋转中心由锐角顶点改成直角顶点，降低了学生首次观察简单的几何图形旋转前后的特点的难度，便于总结；第三，将三角尺放在方格纸上，便于学生观察旋转位置的变化，同时为后面画旋转后的图形做了铺垫；第四，将直接观察换成动手操作，使学生在操作的过程中更能体会旋转中心和各边的运动过程。

（二）学情分析

为了更清楚地了解学情，基于教材分析，笔者编制了几道前测题（略），对我校五年级的部分班级学生（在测试前未进行“图形的运动（三）”学习）进行调查，共150人参与测试。

调查发现：

首先，大部分学生认为转动360°才是旋转，转不满一周的不是旋转。

其次，76%的学生知道顺时针、逆时针方向；62.7%的学生能标出旋转中心，37.3%的学生未能标出旋转中心。通过访谈还发现，未能标出旋转中心的学生中有33人能指出旋转中心。

最后，6.7%的学生能完整地描述旋转过程，77.3%的学生能结合旋转要素不完整描述旋转过程，16%的学生不能描述旋转的过程或描述的内容与旋转无关。

二、教学实践

（一）观察生活实例，认识旋转要素

1.出示有争议的生活实例，引出研究问题

师（出示前测统计结果，见表1）：昨天我们做了个课前小测试，老师把大家的做题情况统计出来了，我们一起来看看。

师：认为钟摆不是旋转的同学，你们是怎么想的？

生1：因为它是左右摆动的，所以不是旋转。

生2：因为它转动的度数不是360°，所以不是旋转。

师：认为钟摆的运动是旋转的同学，你们有什么想说的吗？

生3：钟摆一直绕着一个点转动，所以它的运动是旋转现象，跟它是不是转360°没有关系。

师：到底是不是旋转一周才算是旋转呢？看来大家意见不统一，带着这个疑问，咱们进一步来学习图形的旋转。

师：选择一个你喜欢的例子，然后说一说它是怎么旋转的。

动态展示旋转现象（如图1）：

师：同学们已经初步认识了生活中的旋转现象，想一想，旋转有什么特点呢？

生4：风扇的扇叶是按顺时针方向转的。（涉及方向）

师：你能跟大家说说什么是顺时针旋转吗？

【设计意图：课的开始，教师通过出示前测结果，选择学生熟悉的“不是360°旋转”的例子作为学习研究的素材，从学生存疑的生活例子入手，引发认知冲突，激发学生探究的欲望。】

2.借助钟面，认识旋转三要素

（1）认识旋转要素——旋转方向

师：我们把与时针旋转方向相同的，叫顺时针旋转；与时针旋转方向相反的，叫逆时针旋转。下图（如图2）中，风车和转盘分别是按什么方向旋转的？

师（小结）：通过观察钟面、风车、转盘的旋转可以发现，物体的旋转都是按照一定方向旋转的。

师：除了方向，我们还要关注旋转的什么要素呢？下面我们利用钟面进行研究。方便起见，我们只观察其中一根指针。

【设计意图：以钟面、风车、转盘等物体的旋转为例，引导学生经历观察、对比等过程，使其初步感受物体的旋转是按一定方向进行的。】

（2）认识旋转要素——旋转中心、旋转角度

师（出示课件：钟面上，指针分别从“12”旋转到“1”，从“1”旋转到“3”。如图3所示）：仔细观察，甲钟面从“12”到“1”，乙钟面从“1”到“3”，指针分别是怎么旋转的？

生1：甲、乙两个钟面上的指针都是按顺时针方向旋转的。

生2：都是绕点[O]按顺时针方向旋转。

师（小结）：它们的共同点就是——都是绕着点[O]按顺时针方向旋转的。（说明：点[O]就是它的旋转中心）

师：在旋转过程中有什么不同点呢？

生3：甲钟面是从“12”到“1”，乙钟面是从“1”到“3”。

生4：指针扫过的面不同，叉开的大小不同。（教师规范其语言：旋转角度不同）

师：甲钟面中，从“12”到“1”，指针旋转了多少度？你是怎么知道的？

生5：从“12”到“1”，指针旋转了30°。（绕点[O]顺时针旋转30°）

生6：钟面有12个大格，旋转一周是360°，所以360°÷12=30°

师：看来我们在描述物体的旋转时还得关注它的旋转角度。

师：想一想，怎么样才能清晰、准确地描述钟面指针的旋转呢？

师（小结）：要清晰、准确地描述指针的旋转过程，就要讲清楚三点——指针是绕哪个点旋转的；指针按什么方向旋转；指针旋转了多少度。

师：现在谁愿意来完整地描述，从“12”到“1”，指针是怎样旋转的？

生7：从“12”到“1”，指针绕点[O]按顺时针方向旋转了30°。

师：从“1”到“3”呢？

生8：从“1”到“3”，指针绕点[O]按顺时针方向旋转了60°。

3.再次观察、描述，加深理解

师（出示两个钟面，指针分别从“3”旋转到“6”，从“6”旋转到“12”，图略）：对于这两个钟面指针的旋转过程，你能完整地描述出来吗？

生9：从“3”到“6”，指针绕点[O]按顺时针方向旋转了90°。

生10：从“6”到“12”，指针绕点O按顺时针方向旋转了180°。

【设计意图：通过观察钟面指针的旋转，引导学生探索并认识旋转的三要素，从而激励学生用数学语言描述物体的旋转过程，使其深入理解图形旋转的本质。】

4.动画演示，突破难点

师（出示钟摆运动，如图4所示）：回到我们刚开始上课时留下的问题，钟摆转动是不是在做旋转运动？为什么？

生：钟摆的运动是旋转，因为它是绕着一个中心按照顺时针方向或者逆时针方向旋转的，旋转角度是不确定的。

【设计意图：通过观察钟摆运动的动画演示，让学生清楚地认识到钟摆运动的特点实际上就是“围绕一个点做局部的圆周运动”，并且在摆动的过程中，有按顺时针方向的旋转，也有按逆时针方向的旋转，钟摆旋转的角度是不确定的。】

（二）动手操作，感悟旋转性质，发展学生空间观念

1.研究线段的旋转

（1）模拟操作

师：想一想，假如现在我们把钟面的指针看成一条线段，线段能旋转吗？

师：请你拿出一根小棒，把它看成线段OA，然后在方格纸上试着感受一下，线段可以怎么旋转呢？

（2）画中理解

师（出示练习，如图5所示）：请你画出线段[OA]绕点[O]逆时针旋转90°后的图形，并标出点[A]的对应点[A′]。

（3）辨析深化

师（展示学生作品：作品①完全正确，作品②方向有误——强调方向）：作品①是完全正确的，作品②的方向错了。看来在画图的时候，不仅要关注旋转中心和角度，还得注意旋转的方向。

师（展示学生作品③：线段长度变了——强调性质）：这里还有一个画得不太一样的作品，仔细观察，你有什么想说的？

生：线段的长度变了，这不是旋转。

师：对，旋转前后，虽然线段的位置改变了，但是线段的长度是不变的。

【设计意图：让学生在方格纸上画出线段旋转90°后的图形，经历“模拟‘转—‘画下来”的过程，同时让学生在动手操作中思考并理解旋转的要素，从而为后续学习面的旋转做铺垫。】

2.研究面的旋转

（1）动手操作，类比迁移

出示问题（如图6）：

师：如果增加两条线段，把线段[OA]变成一个三角形，想一想，三角形的旋转和线段的旋转会有什么联系呢？

师：想象一下，三角形绕点O顺时针旋转90°后，它会到什么位置？

师：利用三角形学具在方格纸上绕点O顺时针旋转90°。

师：同桌交流，三角形旋转前后，什么没有变？什么变了？

生1：首先固定O点不动，然后把三角形绕点O顺时针旋转90°。

（课件演示：三角形绕点O顺时针旋转90°）

师：仔细观察三角形旋转前后，什么没有变？什么变了？

生2：三角形的位置变了；每条边都绕点O顺时针旋转了90°。

生3：点O位置不变（旋转中心位置不变）；三角形的形状不变；每条线段的长度不变。

师：旋转前后，旋转中心位置不变，三角形的形状不变；它只是每条边都绕点O顺时针旋转了90°。其实，这个三角形的旋转，我们也可以看成是三角形每一条边（线段）的旋转。

（2）学生想象，发展思维

师：同学们，想象一下，如果三角形AOB继续绕点O顺时针旋转90°两次，会得到什么图案？

（动画演示风车旋转，如图7所示）

【设计意图：从“线段的旋转”迁移到“面的旋转”，让学生经历“想象—操作验证—再次想象”的学习过程，将想象与操作结合，激发学生的空间想象力，发展学生的空间观念，为后续的学习奠定基础。】

（三）应用拓展，感受数学之美

（1）欣赏图案，感受旋转创造的美

出示课件（如图8）：

（2）再次想象，“面”——“体”，拓展思维

师：如果以一条直角边为轴将直角三角形转动一周，想象一下，会得到一个什么样的图形？

生1：还是三角形。

生2：圆。

生3：圆锥。

师（课件动态演示，如图9所示）：想象一下，长方形绕着它的长转动一周，会得到什么样的图形？

图9

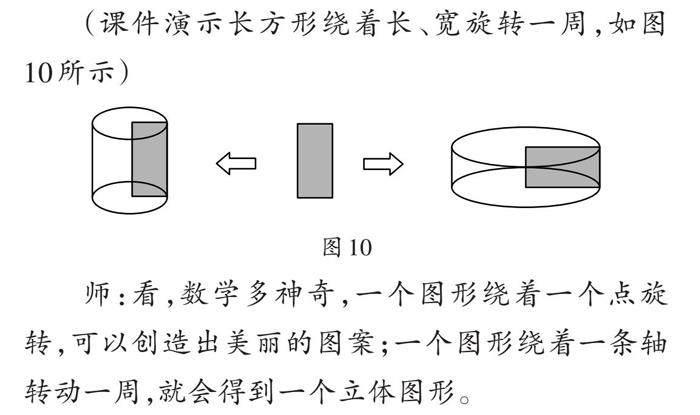
（课件演示长方形绕着长、宽旋转一周，如图10所示）

师：看，数学多神奇，一个图形绕着一个点旋转，可以创造出美丽的图案；一个图形绕着一条轴转动一周，就会得到一个立体图形。

【设计意图：课件动态展示一些基本图形旋转后形成的美丽图案，鼓励学生学会用变化的数学眼光观察、体验旋转的奇妙之处，从而感受到数学之美，体会到生活中处处有数学。展示内容从“绕点的旋转”到“绕轴的旋转”的知识，图形转动一周后形成立体图形，从而激发学生的创造性思维，丰富学生对不同旋转方式的认知。】

学生只有经历动手操作、体验、数学表达、感悟等数学活动过程，才能更有效地发展空间观念素养。为此，教师在教学过程中应有意引导学生经历操作体验等活动，从而帮助学生积累有效的数学活动经验，发展空间观念素养。

（责编 吴美玲）