基于数学思想的空间向量与立体几何问题的解题技巧与方法

牛晓琳

【摘要】空间向量与立体几何作为每年高考命题中的一大主干知识，是高考数学试卷解答题中的重要类型之一.文章借助空间向量与立体几何中的数学思想，从函数与方程思想、分类讨论思想、数形结合思想等入手，通过实例剖析，阐述数学思想的应用技巧与方式，引领并指导数学教学与复习备考.

【关键词】空间向量；立体几何；数学思想；解题应用

引 言

空间向量与立体几何中，重点是利用空间向量来解决有关的立体几何问题，将几何的综合推理和向量的代数运算有机地结合起来，为我们的数学思维活动开辟更加广阔的天地，更好地培养分析问题、解决问题的能力.在具体解决立体几何问题的过程中，往往离不开数学思想方法的应用.

一、函数与方程思想的应用

在立体几何中，通过建立空间直角坐标系，把空间中的线段、角、距离等问题用数表示，然后通过分析变量间的对应关系，建立方程或方程组或者构造方程或方程组，使问题获得解决.有关线段、角度、面积、体积的计算，经常需要用构造方程或建立函数关系式的方法加以解决.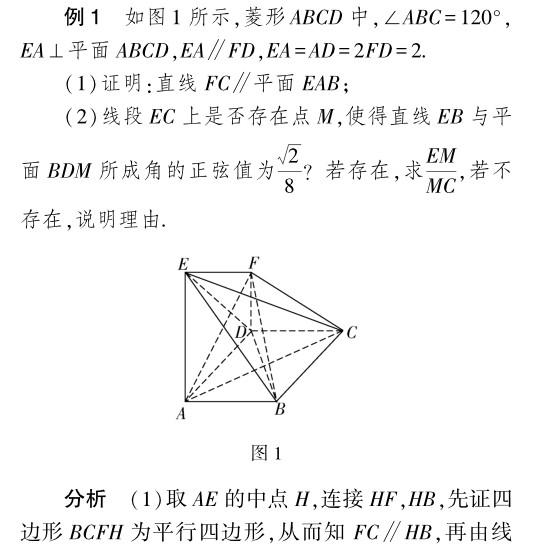

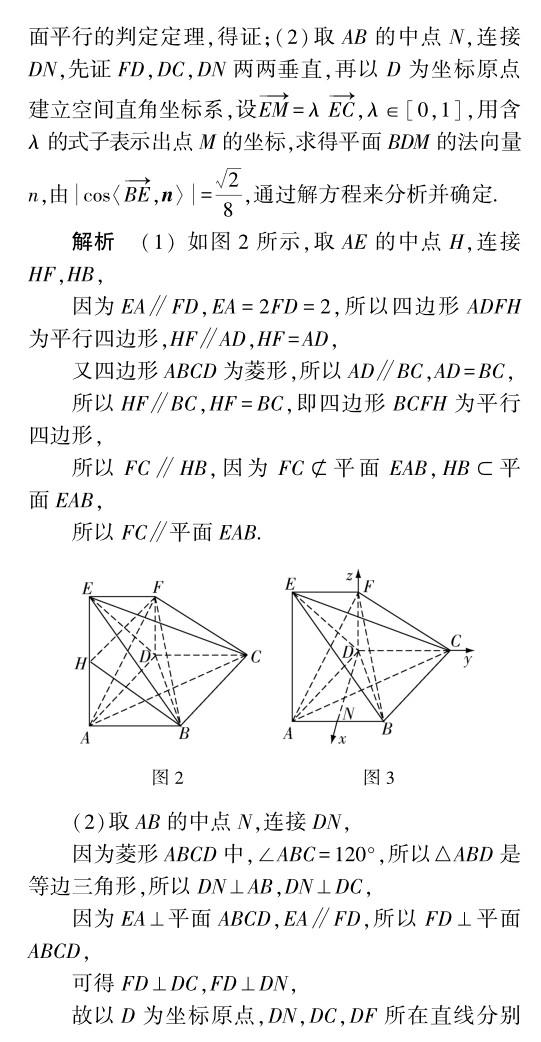
分析 （1）通过合理构建空间直角坐标系，设出线段CP=x，利用两向量坐标的确定，结合垂直关系转化为数量积0，合理构建对应的关系式，再根据方程的根的个数来讨论点的存在性问题；（2）由（1）可知a=2，进而分别求解两个半平面的法向量，利用数量积公式来求解对应的二面角的平面角的余弦值即可.

解析 （1）建立如图5所示的空间直角坐标系，其中直线DC为x轴，直线DA为y轴，直线DD1为z轴.

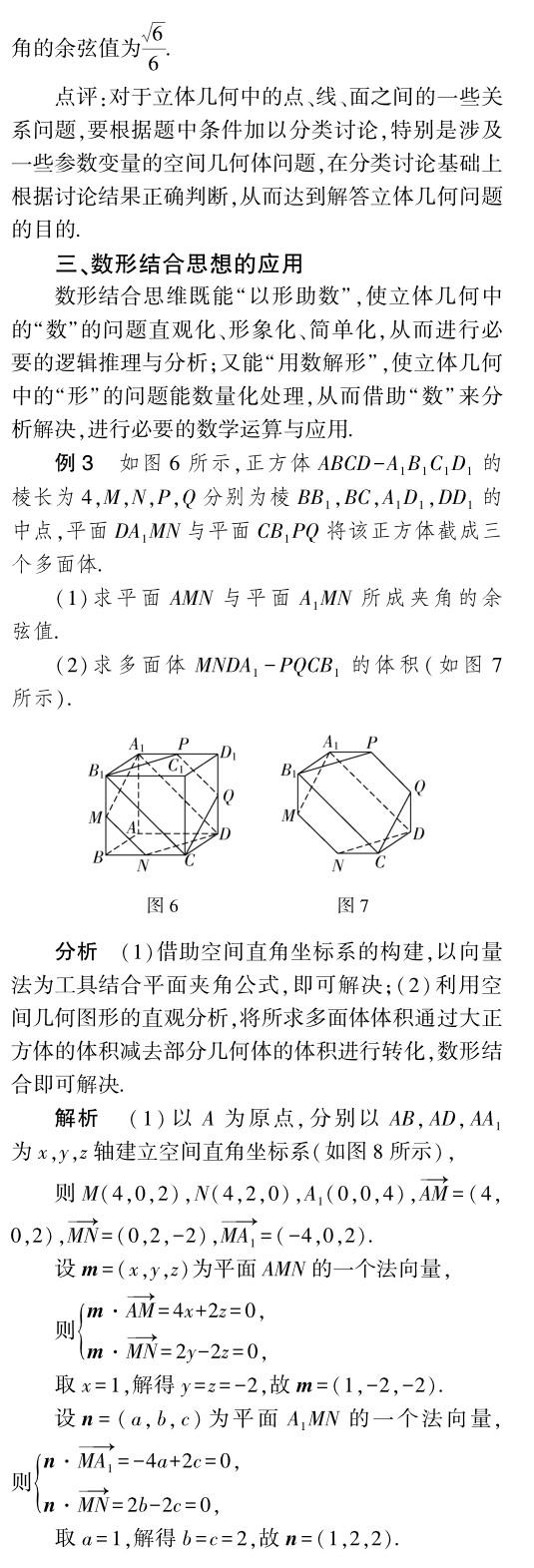
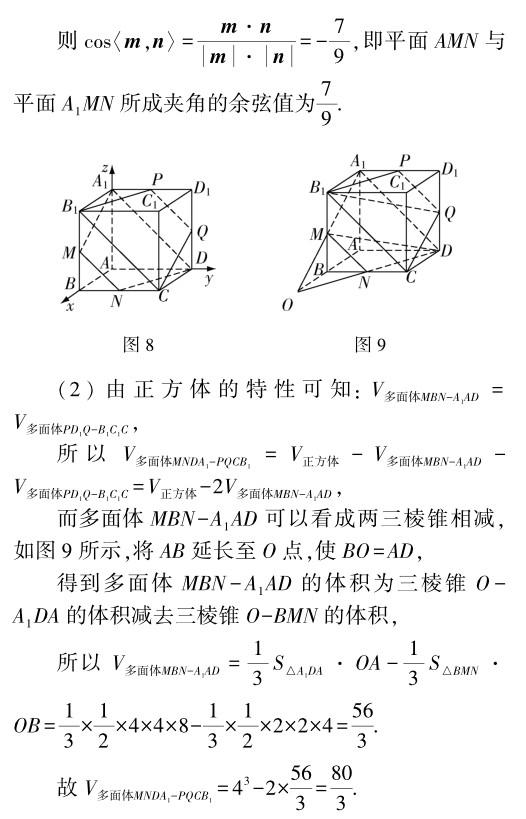
点评：立体几何问题的空间想象与直观图形，都离不开数形结合思想的应用，由题设条件中的“数”与“形”的信息结合，又结合逻辑推理或数学运算这两个层面“数”与“形”的应用来达到目的，是解决立体几何问题中最为常见的技巧.

结 语

数学思想比数学概念更具有抽象概括水平，后者比前者更具有具体性、丰富性，前者比后者更具有深刻性、拓展性.在空间向量与立体几何的综合问题中，结合基本知识点与丰富的数学思想方法的交汇与融合，总结其一般解题技巧与策略，合理应用数学思想方法引领，全面提升数学思维品质与数学基本能力，必然会达到事半功倍的良好效果.

【参考文献】

[1]王婷婷.高中数学“立体几何初步”单元教学研究[D].呼和浩特：内蒙古师范大学，2023.

[2]张林华.活用数学化归思想提升立几解题能力：以2022年浙江省数学高考第19题为例[J].中学教研（数学），2022（12）：34-36.

[3]张佳媛.高中数学人教A版新旧教材“立体几何”部分的比较研究[D].哈尔滨：哈尔滨师范大学，2021.