数学建模:理论与实践
王娇 张灿

基金项目:2022年度安徽省芜湖市教学研究重点课题“双减背景下促进核心素养发展的数学实验教学实践与研究”(项目编号:2022JK062).
摘 要:在初中数学中,综合与实践课常以数学广角、数学活动或数学习题的方式编写,本节课以全等三角形的证明方法为理论,通过数学实验的方式,引导学生通过操作与实践,从“坐中学”转变为“做中学”,从“听数学”转变为“主动探究”.文章以“手拉手模型之全等三角形”的教学设计为例,阐述了如何动手“做”数学.
关键词:数学实验;动手操作;“做”数学;数学建模
史宁中教授在《义务教育数学课程标准(2022年版)解读》中提出,义务教育数学课程改革面临的问题是“综合与实践”领域的教学没有得到有效落实.针对此问题,笔者尝试从书本习题出发,将三角形全等的理论知识与学生动手实践相结合,培养学生理论与实践相结合,建立数学模型思想.
在实践活动中,数学实验是目前在教学中比较行之有效的教学形式,通过引导学生动手动脑“做”数学来达到教学目标的实现.课堂上用模型、测量、计算机软件,激发学生的学习热情,帮助学生从以往的教学中的“听数学”“当观众”转变为“主动探究”“当演员”,变“机械学习”为“自己研究”.学生在实验过程中,发挥内驱力,形成了良好的数学思维,尤其是在这一过程中,教师与学生之间的互动,使学生了解数学知识、数学体系的建构过程,对所学的知识产生兴趣,打破初中数学学习刻板的印象.
1 复习旧知,引入新课
教师帮助学生构建全等三角形知识框图,探讨从哪些角度证明两个三角形全等.并给出课本习题,学生练习,引出本节课实践内容.
【设计说明】对于学生来说,全等三角形是学生刚刚学过的知识,并不陌生,通过回顾旧知的方式帮助学生为全等三角形知识的应用铺设台阶.
2 实验探究,验证结论
2.1 等边三角形中的手拉手问题
实验1:
(1)请拿起手边的两个等边三角形,分清三角形的左底角与右底角和顶点,将两个三角形的顶点重合;
(2)将一个三角形绕顶点旋转不同的角度,观察并记录拼接后的图形;
(3)用笔将两个三角形的左底角连接,右底角连接,并标注字母;
(4)用量角器测量由顶点和两左底角(或两右底角)构成三角形的内角.
(电脑演示:三角形旋转后,测得顶点和两左底角(或两右底角)构成三角形的内角以及边长)
问题1
(1)根据测量结果,你发现这两个三角形有什么关系?
(2)当一个三角形旋转到任意位置,两个三角形全等是否仍然成立?你能应用全等三角形的知识证明它吗?
【设计说明】让学生实际操作,感受三角形的旋转过程,记录相对应的位置.通过学生测量、教师利用几何画板演示测量角度和线段长度,引导学生猜想两个三角形的关系,并从理论上对两个三角形的全等加以证明,从中体会变化中存在的不变关系.
小结:当两个等边三角形的顶点重合时,运动其中一个三角形,连接线段,所得的△ABE和△CBD形状发生变化,但两个三角形的全等关系不变,说明运动图形中存在不变性.
实验2
(1)請拿起两个任意形状的三角形,确定好两三角形的顶角和底角,将两个三角形的顶角重合;
(2)将一个三角形绕顶点旋转不同的角度,观察并记录拼接后的图形;
(3)用笔将两个三角形的左底角连接,右底角连接,并标注字母;
(4)用量角器测量由顶点和两左底角(或两右底角)构成三角形的内角.
(电脑演示:三角形旋转后,两三角形形状)
问题2
(1)从记录的数据看,实验1得出的两个三角形还全等吗?为什么?
(2)这说明两图形运动的不变性是有条件的,要想实现两个三角形的全等,对这两个三角形的性状有什么要求?
【设计说明】学生动手操作,连线、度量、猜想,得出要想保证两个三角形全等这条性质,两个三角形的形状是有要求的,体会变化中存在的不变关系需要满足的条件.
2.2 等腰三角形中的手拉手问题
实验3
(1)请拿起手边的两个等腰三角形,确定好两三角形的顶角和底角,将两个三角形的顶角重合;
(2)将一个三角形绕顶点旋转不同的角度,观察并记录拼接后的图形;
(3)用笔将两个三角形的左底角连接,右底角连接,并标注字母;
(4)用量角器测量由顶点和两左底角(或两右底角)构成三角形的内角.
(电脑演示:三角形旋转后,两三角形形状)
问题3 实验3得出的两个三角形全等吗?如何证明?若将等腰三角形换成等腰直角三角形还成立吗?
【设计说明】将两个等边三角形换成等腰三角形,学生通过操作、猜想、证明,感受到通过旋转两个等边三角形得出的结论,可推广到旋转一般的等腰三角形.
3 抽象概念,生成知识
3.1 形成概念
问题4 这种运动图形中存在的不变性,针对的两个三角形需要满足什么特征?得出的是什么结论?
特征:等腰三角形(或等边三角形、等腰直角三角形、正方形)共顶点,等顶角.
结论:存在两三角形全等.
如果我们形象地把一个等腰三角形的顶点看作“头”,左底角看成“左手”,右底角看成“右手”,那么可描述成“头对头,左手拉左手,右手拉右手”,那么这种能得到全等的图形的模型就叫做“手拉手模型”.
【设计说明】让学生经历观察、动手操作等一系列活动,提高学生合情推理和演绎推理的能力,让学生用自己的语言概括出“手拉手模型”的概念.
3.2 概念辨析
练习1 如图1,已知AC=AD,AB⊥BC,∠BAE=12∠CAD,利用“手拉手模型”构造全等三角形.
图1
【设计说明】通过让学生构建左手拉左手,右手拉右手,更好地理解全等三角形的作法.
练习2 如图2,将两等边三角形旋转至A,B,D在一条直线的位置关系,你能得出哪几组三角形全等?
图2
追问 若连接FG,你还能得出什么结论?连接HB呢?
FG∥BD,∠CHF=60°,HB平分∠FHG.
【设计说明】通过实验操作,让学生明白当关注更多的点,就可以得出除上述实验得到的全等三角形外其他两组全等三角形,为接下来“手拉手模型”知识的拓展做好铺垫工作.
3.3 知识延伸
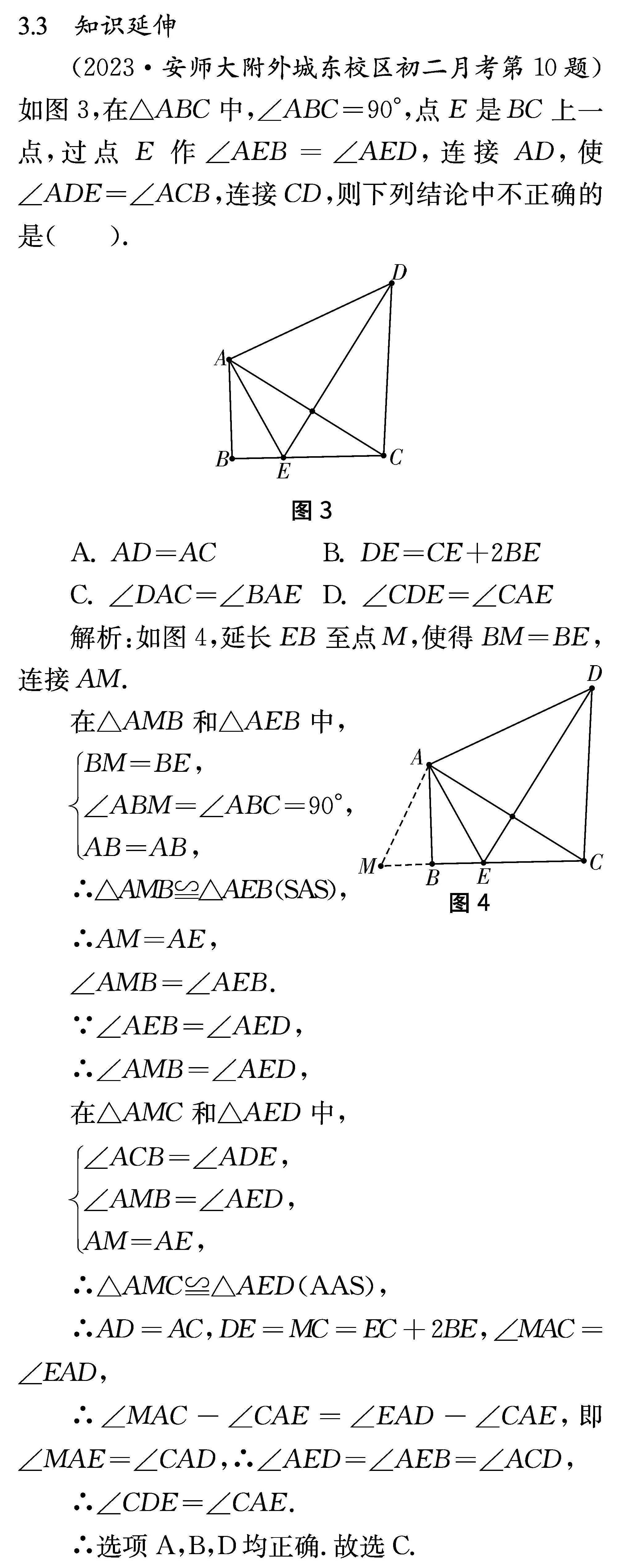
^^(2023·安师大附外城东校区初二月考第10题)&&如图3,在△ABC中,∠ABC=90°,点E是BC上一点,过点E作∠AEB=∠AED,连接AD,使∠ADE=∠ACB,连接CD,则下列结论中不正确的是( ).
图3
A. AD=AC
B. DE=CE+2BE
C. ∠DAC=∠BAE
D. ∠CDE=∠CAE
解析:如图4,延长EB至点M,使得BM=BE,连接AM.
在△AMB和△AEB中,
图4
BM=BE,
∠ABM=∠ABC=90°,
AB=AB,
∴△AMB≌△AEB(SAS),
∴AM=AE,
∠AMB=∠AEB.
∵∠AEB=∠AED,
∴∠AMB=∠AED,
在△AMC和△AED中,
∠ACB=∠ADE,
∠AMB=∠AED,
AM=AE,
∴△AMC≌△AED(AAS),
∴AD=AC,DE=MC=EC+2BE,∠MAC=∠EAD,
∴∠MAC-∠CAE=∠EAD-∠CAE,即∠MAE=∠CAD,∴∠AED=∠AEB=∠ACD,
∴∠CDE=∠CAE.
∴选项A,B,D均正确.故选C.
【设计说明】通过这个问题,让学生明白在遇到问题时,可以尝试从寻找两个等腰三角形的角度来构建“手拉手模型”,进一步体会“变”与“不变”的数学思想.
4 归纳总结,深度思考
问题5
(1)如何判别图形是“手拉手模型”?
(2)由“手拉手模型”可以得出哪两个三角形全等?
(3)图形在旋转过程中得出的三角形全等用到了什么数学思想?
(4)通过今天的学习,你积累了哪些学习经验?
(5)你还有哪些疑惑?
【设计说明】通过提出一系列问题,进行有针对性的小结,帮助学生回顾本节课的学习过程,构建本节课的知识框架,提炼本节课的重难点,从而更好地内化本节课内容.
5 教学反思
本节课是义务教育教科书人教版八年级上册“全等三角形”应用的内容,之前已经学习了三角形全等的判定以及角平分线的性质,因此,本节课作为全等三角形的应用,有巩固相关知识的目的.笔者根据学生喜欢动手的特征,选择不同的三角形纸片,让学生在课堂中动手操作,得出图形,再对自己画的图形观察、度量、猜想、证明,体会“手拉手模型”得出的两个三角形的由来.在数学课堂中,教师尊重学生的主体地位,从学生已有的认知发展水平、数学知识及数学思维能力出发,引导学生对图形作创造性的构建,体会图形中存在的不变性.
《义务教育数学课程标准(2022年版)》指出:“教学活动应注重启发式,激发学生的学习兴趣,引发学生积极思考,鼓励学生质疑问题,引导学生在真实情境中发现问题和提出问题,利用观察、猜测、实验、计算、推理、验证、数据分析、直观想象等方法分析问题和解决问题.”学生在学习新知的过程中,经历了动手操作、观察归纳,从两个具体的三角形中找出全等三角形,归纳两个三角形全等时满足的条件,建立数学模型思想.
参考文献
[1] 陈超.数学实验在初中数学教学中的运用研究[J].理科爱好者,2022(3):44-46
[2] 董林偉.数学实验:促进初中生数学学习的一种有效方式[J].中国数学教育,2012(5):2-5
[3] 林群.义务教育教科书(人教版)数学八年级上册[M].北京:人民教育出版社.
[4] 史宁中,曹一鸣.义务教育数学课程标准(2022年版)解读[M].北京:北京师范大学出版社,2022.

