授人以鱼，授人以渔

李燕萍

【摘要】初中教学中有很多知识都渗透着数形结合思想，特别是函数的章节，但是学生往往很难将两者联系到一起，导致学生畏惧函数类型的题目，所以如何在教学中渗透数形结合值得我们探索.

【关键词】数形结合；初中教学；课堂教学

古人云：“授人以鱼不如授人以渔.”所以教师在讲授知识的同时更要告诉学生思考问题的方法.数形结合是一个重要的数学思想，能够使学生发现知识点之间的关联，找到思考问题的方向，故在初中数学教学中教师应重视数形结合思想的渗透.

平面直角坐标系是学习函数的基础，平面直角坐标系将几何和代数联系起来，学生可以通过观察函数图象和坐标轴的交点来解方程，可以通过观察函数图象的形状来研究函数的性质.故在平面直角坐标系教学中的数形结合思想的渗透显得尤为重要.下面将以“平面直角坐标系——用坐标刻画一个简单的图形”这一课为例阐述如何在教学中渗透数形结合思想.

1 研判学情，决定教学策略

教学应以学生为主，这节课前学生已掌握平面直角坐标系的基础知识，会根据点在平面直角坐标系中的位置写出点的坐标，会根据点的坐标在平面直角坐标系中描出点的位置.同时班级里小组建设较为成熟，可以顺利开展小组合作，在教学过程中可以考虑适当进行小组合作.

2 研究教材，明确教学目标

教师应深入挖掘教材的内容，整理出有关于数形结合的内容，引导学生在探究中慢慢形成数形结合的思想[1].这节课是课本中的一个例题，为什么我们要用一节课的时间来研究它？前面的课时中我们学习了用坐标刻画一个点、一条线段，而这堂课研究用坐标刻画一个简单的图形，层层递进地让学生感受数形结合的思想.因此确定这节课的目标是：①引导学生能在直角坐标系中用坐标刻画一个简单图形，对给定的正方形，会选择合适的直角坐标系，写出它的顶点坐标；②通过用“数”刻画“形”以及用“形”直观地描述“数”来让学生辩证地体会、理解数形结合思想；③使学生体会数学抽象之下的应用广泛性，领会数形结合思想的应用价值.

3 理清思路，设计教学过程

这节课的思路是先提出问题：能否用坐标刻画一个简单的图形？引起学生的学习兴趣，带着问题学习.再提出问题：能否用坐标刻画一个正方形？接着是刻画一个长方形、三角形.根据这个思路设计以下的教学过程.

3.1 巩固基础知识，奠基后续学习

前两节课学习了平面直角坐标系中用坐标刻画一个点，利用以下的问题复习点在平面直角坐标系中不同位置坐标的特点.

（1）在前面一节课的学习中，我们用什么方法来确定平面内点的位置？

（2）在平面直角坐标系中，每一象限的点的坐标符号是什么？

（3）x轴和y轴上的点的坐标有什么特点？

“平面直角坐标系”的内容比较抽象，尤其是坐标的特点，如果只是死记硬背，不仅使学生难以理解，也容易忘记，影响学生的学习积极性.所以在前期的教学中利用数形结合的思想，让学生观察坐标系上的点和坐标，归纳不同位置的點的坐标特点，不仅更易理解，还能感受数形结合思想的重要性.

3.2 构建知识脉络，实现深度学习

课堂教学应循序渐进，教师设置合理的教学内容，使学生在问题的探究中理解数形结合思想，促进核心素养的形成.可在课前先布置学生完成以下题目，课堂上投影展示学生作品.

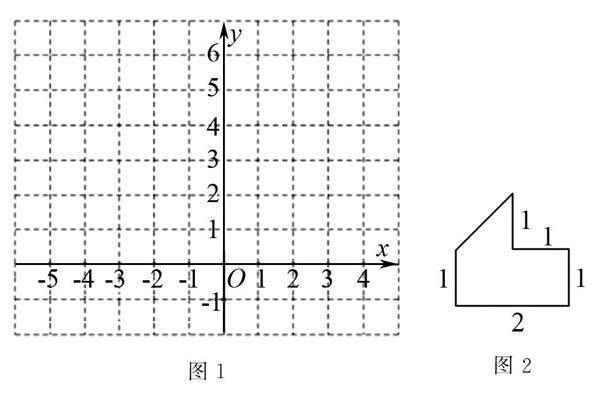
（1）如图1，在平面直角坐标系中描出下列点，并将这些点用线段依次连接起来．

（-5，0），（-4，3），（-3，0），（-2，3），（-1，0），（-5，0）．

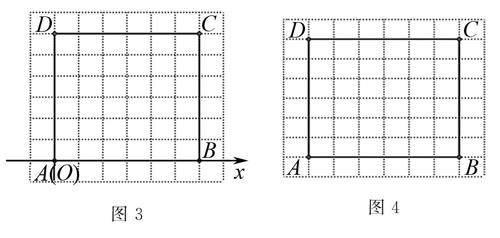
观察得到的图形如图2，你觉得它像什么？求出所得到图形的面积．

（2）请你用这部分已学的内容，向你的伙伴准确描述右边的图形.

教师问；“这组坐标刻画了一个类似什么的图形？大家画出的图形都一样吗？”引导学生归纳：“形”描述“数”.

第（2）小题有学生会用“三角形加长方形”或“算面积”来描述这个图形，教师可问：“能用上述两种办法来描述这个图形吗？这样描述后图形确定了吗？”引导学生发现这两种描述方式无法确定图形的形状.展示学生的作品：“有同学用平面直角坐标系中点的坐标来描述这个图形.”同时根据学生所写的坐标描出相应的点，并用线段依次连接.引导学生归纳：“数”刻画“形”.教师进一步引导学生归纳：刻画一个简单的图形需要关键点的坐标.根据这两道题，学生得出在平面直角坐标系中“数”与“形”可以互相描述.教师提出问题：“我们能否用坐标来刻画一个正方形？”并设计问题1.

问题1 探究：

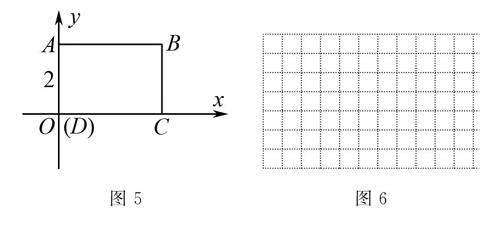
（1）图3，如果以点A为原点，AB所在直线为x轴，建立平面直角坐标系，那么y轴是哪条直线？请画出来，并写出正方形的顶点A，B，C，D的坐标．

（2）在图4中，请另建立一个平面直角坐标系，这时正方形的顶点A，B，C，D的坐标又分别是多少？

第（1）小题：教师引导学生归纳要建立平面直角坐标系首先应确定原点，利用y轴与x轴、原点之间的位置关系，确定x轴、y轴，并引导学生得出建立这个平面直角坐标系是依据正方形的内角是90°.

第（2）小题：教师问：“你能否建立另一个平面直角坐标系，并写出正方形的四个顶点的坐标吗？”让学生先独立思考，再进行小组讨论完成以下任务：①小组讨论能建立的平面直角坐标系有哪几种？②组长检查组员建立平面直角坐标系后顶点坐标的正确与否.

教师问：“你们可以建立几种平面直角坐标系？”请小组进行展示.教师引导学生观察他们所建立的平面直角坐标系可以以四个顶点、边的中点或正方形的中心为原点，以与正方形的边平行或垂直的直线为坐标轴建立的.让学生在建立平面直角坐标系的同时，感受正方形可以用坐标来刻画，进一步理解数形结合的思想.

3.3 渗透数学思想，提高学习能力

一道题的讲解不能只限于解决问题，还应该挖掘其有价值的部分，问题1还可以引导学生发现坐标的数量关系体现了图形的性质，进而对数形结合的思想有更深入的理解.接下来进行以下追问：

追问1：“不管如何建立平面直角坐标系，描述的是否都是同一个正方形？同一个点的坐标为什么不同？”

追问2：“观察出来的坐标有什么特点？”教师引导学生：①先观察A，D的坐标，再观察B，C的坐标，得出横坐标相等的点所在的直线平行于y轴；②先观察A，B的坐标，再观察C，D的坐标得出纵坐标相等的点所在的直线平行于x轴；③由坐标可得到正方形的边长为6.

归纳：①建立平面直角坐标系需先确定原点、x轴、y轴；②同一个点在不同的坐标系下坐标不同；③坐标的数量关系可以刻画图形的性质.

为了让学生进一步感受坐标可以确定一个图形的形状和大小，可设计题目：给出四个点的坐标：（1，1），（1，7），（7，7），（7，1），用线段依次连接，观察是否是正方形？这个正方形的大小是否也确定了？

3.4 分析解题思路，发展学生思维

提出问题：“是否也能用坐标来描述长方形？需要用几个点？”并设计问题2引导学生用数形结合的思想分析题目，进而发展学生的思维.

问题2 在平面直角坐标系中，长方形ABCD的长AB为3，宽BC为2．

（1）如图5，若顶点D与原点重合，请你写出A、B、C、D四点的坐标．

（2）如图6，若A（-1，3），D（-1，1），点B在第一象限，请你写出点C的坐标．

第（2）小题，引导学生先建立平面直角坐标系，再描出点A，D，由点B在第一象限，BC=2，找到点B的位置，进而补全长方形，猜想点C的位置和坐标.教师引导学生分析：①由A和D的坐标，可得AD⊥x轴，AB∥x轴；②由AB∥x轴，AB=3，点B在第一象限，可得A，B纵坐标相等，故B（2，3）；③由BC∥y轴，BC=2，可得B，C横坐标相等，故C（2，1）.

归纳：①建立平面直角坐标系；②描出已知点；③分析待确定点的位置.接着在问题1、问题2的基础上做一个提升，设计问题3.

问题3 已知点A（2，3），B（2，1），∠ABC=90°，△ABC的面积是3，求符合条件的点C的坐标.

教师引导学生做以下分析：①在坐标系描出点A和点B；②由点A和点B的坐标可得点A，B的横坐标相同，所以AB⊥x轴，再由∠ABC=90°，可得BC∥x轴，从而得到B，C两点的纵坐标相等，确定点C的纵坐标为1；③点C可能在点B左边或B右边，应该需要分类讨论；④由△ABC的面积是3和高AB=2，可得底BC=3.当点C在点B左边时，得到C（-1，1）；当点C在点B左边时，得到C（5，1）.

归纳：①解题思路：建、描、画、算、定；②对未确定的图形应考虑分类讨论.

4 结语

数学思想不是说一句“这就是数形结合思想”就可以的，教学中要注意随时渗透，随时揭示，多问“为什么？”如這节课中不同的建系方法刻画的都是同一个正方形，正方形的边长不变，所以可以通过引导学生观察写出的坐标的数量上的特征，得到图形上的特征，最后归纳总结：坐标的数量关系可以刻画图形的性质.从而渗透数形结合的思想.

参考文献：

[1]李莉.数形结合思想在初中数学课堂教学中的渗透[J].数理天地（初中版），2023（15）：62-64.