数学核心素养视角下的单元—课时教学设计

曹雪芹 陈志恩

摘 要：单元教学设计是围绕单元主题对知识进行深层挖掘和意义联结，进而实现对知识的结构化处理。它的开展可以帮助学生系统地理解常用数学知识之间的联系，形成整体知识框架，是培养学生核心素养的有力工具。由单元到课时的教学设计，是将单元目标分解到每一课时，这种教学设计不仅可以体现数学的层次性，还可以强化学生的逻辑思维能力，从而有利于学生素养目标的达成。本文将以“数列”单元为例，以核心素养为引领，探究单元—课时教学设计。

关键词：核心素养；单元—课时教学；数列

《普通高中数学课程标准（2017年版）》（以下简称“新课标”）指出：必须将核心素养与数学课堂有机融合；此外，教学设计要改变零散的课时设计，从整体上剖析课程内容，确定单元主题，制定教学目标，围绕核心素养设计教学活动。在此基础上再设计课时教学，可以从整体上明晰数学知识间的联系、掌握数学思想方法、把握数学的本质，系统把控数学教学活动，提升学生的数学核心素养。

1 理解数学，围绕核心素养分析单元教学内容

分析单元教学内容时须以核心素养为引领，以全局为视角理解数學。具体可以先利用知识框图罗列本单元内容，之后围绕知识的本质、上下位关系［1］、蕴含的思想及指向的核心素养这条主线展开分析，在此基础上明确教学重点。

1.1 数列单元知识框图

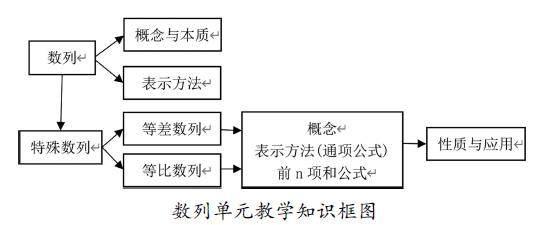
“数列”单元主要包括：数列概念、等差数列、等比数列。首先，教学时教师应先设置具体情境，使学生发现共性并抽象出数列的定义与实质（特殊函数），总之要让学生经过第一节的学习，理解什么是数列及应从哪些方面研究数列［2］；其次，对两类特殊数列也可以从概念、通项公式等来研究，考虑到二者的相似性，应将重点指向等差数列，等比数列类比来学习；最后，再对两种数列的性质及应用做深入研究。由以上分析，绘制如下的单元知识框图：

数列单元教学知识框图

1.2 数列单元知识的本质

数列的本质是定义在正整数集上的特殊函数，可以借助函数来理解数学，例如联系函数的性质探究数列的性质、解决新情境中的题目等。其从本质出发学习新知的方法能使学生理解知识背后的逻辑，促进核心素养的发展。

1.3 数列单元知识的上下位关系

在高一时学生已经对函数掌握了一般的研究方法，教学时教师应有意识地引导学生用函数的思想观点来研究数列。此外本单元的知识又是后续学习“数列极限”的前提，所以数列单元既承接前面又启发后面的知识，有利于学生以全局为视角明晰知识间的联系。

1.4 数列单元知识蕴含的思想方法

首先，类比思想贯穿单元始终，例如类比等差数列的定义归纳等比数列的定义；类比函数知识解决新情境中数列相关的题目等。其次，函数与方程的思想也有体现，例如解题时，启发学生由已知条件及相关公式建立方程组，求解未知数。最后，还涉及特殊到一般的思想，如本单元先探究特殊数列，然后再将特殊数列的思维方式运用到一般数列的研究中。

1.5 数列单元重点培养的核心素养

先从具体情境中归纳共同属性并抽象出概念，发展数学抽象素养；接着通过仔细观察实例中数列各项间的关系，抽象出两种数列模型，培养直观想象和简单的建模素养；最后，经历公式的推理活动，发展逻辑推理和数学运算素养。

1.6 数列单元的教学重点

教学重点主要有三个，一是理解数列的概念和性质，并将其迁移到新情境中；二是渗透类比、方程与函数、特殊到一般等思想；三是培养本单元所涉及的核心素养。

2 了解学生，制定单元—课时教学目标

教学目标须以学生的现有认知为基础，以核心素养为导向，并借助内容的分析明确单元目标。之后将其分解到具体课时，并使单元与课时目标有机融合，以保证课时目标的积累会促成单元目标的实现。

2.1 学情分析，明确难点

学情分析应注意两点：一是明晰学生的现有认知（包括知识、能力及思维方面）；二是结合教学目标，预设学生实现由现有认知到目标认知的过程中可能遇到的困难。然后基于学情分析明确教学难点。

（1）学生的现有认知。此前学生已经学习过函数相关知识，掌握了一定的思想方法，具备了数学运算、推理及简单的建模能力。

（2）可能遇到的困难。首先，采用类比法学习两种特殊数列时，学生对概念、通项公式的类比归纳容易产生困难，教师可以设置“问题链”帮助学生探究。其次，公式的推导难度较大，教师要鼓励学生大胆猜想，勇于探索。最后，数列中有些题目涉及知识点较多，考查学生综合能力，解决起来较为困难，教师要注重启发和指导。

（3）单元教学难点。通项及前n项和公式的推导及其在新情境题目中的运用。

2.2 数列单元教学目标的制定

目标的制定要运用可测的行为动词，还应考虑学生有哪些表现就达到了预期效果，以保证教学目标可操作和测量。此外要遵循“两结合”原则：过程与结果、显性目标与隐性目标相结合，如“经历某种活动（过程），能解决某些问题（显性目标、结果），发展和培养思维方法或关键能力（隐性目标、结果）”的表述，本单元目标包括以下内容。

（1）用自己的语言描述数列的定义和本质；通过观察数列各项之间的规律，能用公式加以表示；反之也能根据公式写出数列的某一项，会进行两者间的转化。

（2）能由具体实例抽象出数学模型，并在新情境题目中加以应用，培养建模素养。

（3）将特殊数列的研究内容和思路运用于研究一般数列，体会特殊到一般的思想。

（4）由具体情境抽象数列，并观察取值特点写出表达式，培养直观想象和数学抽象素养。

（5）能概括出两种数列的定义、通项公式，学会公式的推导及在新情境题目中加以运用。

（6）在推导数列通项的过程中，强化学生的推理能力。

（7）感受数学来源于生活又回归于生活，提高学生的探索兴致。

（8）经历公式的推理活动，并将其运用到新情境中。

（9）通过前n项和公式的推导活动，提升运算和推理素养。

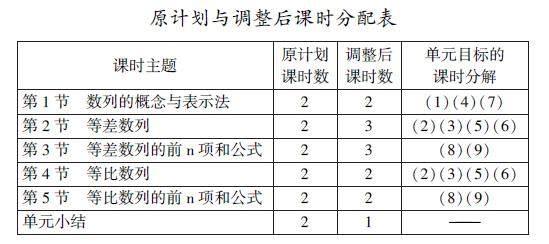
2.3 数列单元教学目标的课时分解

单元教学目标只有在分解到具体课时才能得以落实。按照新课标，完成本单元需12课时，但考虑到学生核心素养的培养，本单元对课时做了相应调整。等差数列一节课由原来的2课时增加到3课时；单元小结是对整个单元知识的归纳和总结，难度相对较小，因此课时由原来2课时减少为1课时。另外，将2.2中制定的单元教学目标分解到具体课时，具体见下表。

3 理解教学，预设单元—课时教学过程

由单元到课时，先将单元目标重难点分解到课时，再设计课堂教学过程，以体现知识的层次性，促成单元目标的实现。设计过程中要突出“两个导向”：以问题链为导向；以知识产生和学生思维发展过程为导向。同时凸显“三个转向”：由结果转向过程，强调学生参与；由知识链转向问题链，注重自我建构；由封闭转向开放，培养创新素养［36］。

下面以等比数列第1课时为例预设教学过程：

3.1 单元目标重难点分解到课时

“等比数列”第1课时主要对应单元目标的二、五、六，具体到课时目标为：（1）类比等差数列的定义归纳等比数列的定义，提升归纳类比能力；（2）经历公式的推理活动，体会“猜想—证明—结论”的探究过程，培养数学运算、推理素养及严谨的思维；（3）在新情境的题目中应用知识，培养问题解决能力。

课时重点是等比数列的定义、通项公式；难点为公式的推理及在新情境题目中的应用。

3.2 教学过程设计

3.2.1 抛出问题，设置悬念

问题导入：还记得等差数列的特征吗？类比等差数列前后两项之差的规律性，前后两项的其他运算能否构成其他值得研究的数列呢？

设计意图：以问题导入的形式激发学生的原有认知，以为新知识的学习和知识体系的构建做铺垫。

3.2.2 问题引领，类比探究

情境1：观看视频——细胞分裂过程。

问题1：一个细胞经过各次分裂产生的后代数目依次是什么？

活动：学生思考：2，4，8，16，…

情境2：古巴比伦时期的泥板上记载了如下数列：

91，92，93，…，910

12，14，18，…，11024

问题2：类比等差数列的特征，以上数列的取值有何规律？采取何种运算才能得到它们的共同特征？

活动：学生思考交流，教师总结归纳，从而引出课时主题，呈现知识背景。

设计意图：从具体实例让学生抽象模型，用问题链引出主题，培养抽象思维和提问能力。

問题3：结合上述规律及等差数列的定义归纳等比数列的定义。

问题4：根据等差数列的符号语言，如何用数学符号描述等比数列？

活动：尝试归纳anan-1=q；

问题5：公差可取任意值，那公比的取值范围呢？带着问题做思考题：判断以下是否为等比数列，如果是请写出公比；不是请解释原因：

①1，5，25，125，…②2，-4，8，-16，…③1，0，1，0，….

活动：合作探究得q≠0.

设计意图：通过问题链及类比思想引导学生归纳定义，注重学生参与，体现了由结果转向过程的设计；思考题让学生自己发现定义中的要点，以加深理解。

问题6：由定义猜想等比数列的通项应该是怎样的公式？

活动：由a2a1=q，a3a2=q，a4a3=q，…猜想

an=a1·qn-1（nN）（1）

问题7：仿照等差数列通项公式的推理方法证明猜想的正确性？

活动：师生交流给予严谨的证明并总结方法——累乘法。

设计意图：采用类比法，提高归纳类比能力；经历“猜想—证明—结论”的探究过程，体会数学是一门有理有据的学科，提升数学运算、推理素养。此外由公式（1）共有四个未知数，提醒学生“知三求一”，渗透方程与函数思想。

3.2.3 小试牛刀，学以致用

例题：等比数列an中a4=48，a4=12，求a5.

变式：等比数列an的公比为q，第m项为am，请自己设问并解决。

活动：例题引导学生分析解答；变式训练先组内探讨，之后全班交流，总结评价。

设计意图：让学生在新情境的题目中运用知识，加深理解，并渗透方程与函数思想。变式训练采取自己设问并解决的方式，锻炼学生的创新思维。

3.2.4 课堂总结，形成框架

问题8：收获了哪些知识？

概念、通项公式及其推导和应用。

问题9：运用了哪些思想方法？

类比、方程与函数、特殊到一般的思想；探究问题时采用“猜想—证明—得出结论”的方法。

设计意图：从知识、思想和方法三方面小结，争取授之以渔，发展核心素养。

3.2.5 布置作业，自我检测

必做：习题1、习题2、习题3；选做：习题4、习题5。

课外：搜集生活中等比数列的实例。

设计意图：分层作业使不同的学生在数学上有不同的发展；扩展题的设置由封闭转向开放，培养学生信息搜集能力，提高综合素养。

3.3 教学反思

本课时聚焦学生的主动参与、自我建构，组织教学时既立足于教材，又超越教材，通过“问题链”指导学生大胆猜想，激发创新潜能。

本案例与传统的教学设计的差异主要有：（1）与传统的课时设计不同，本案例以学生为主体，鼓励学生大胆猜想，教师设置合理的“问题链”，引导学生类比等差数列来探究等比数列相关内容。体现了单元—课时设计更加注重学生的参与和自我建构；更加注重知识的系统性和联结性。（2）关于公式的推导，传统教学多采用类比法予以证明，但本文以全局为视角，让学生经历“猜想—证明—结论”的探究过程，提升问题探究能力。（3）本案例强调用函数的观点来解决相应问题，注重挖掘知识本质，提升核心素养。

参考文献：

［1］吕世虎，杨婷，吴振英.数学单元教学设计的内涵、特征以及基本操作步骤［J］.当代教育与文化，2016，8（04）：4146.

［2］董强.高中数学“数列”单元教学设计研究［D］.西北师范大学，2016.

［3］刘春艳.聚焦核心素养的单元教学设计——以高中“平面向量的运算”单元为例［J］.数学通报，2020，59（07）：4953.

［4］普通高中教科书教师教学用书.数学：选择性必修.第二册：Ａ版［M］.北京：人民教育出版社，2020.

［5］方长林.聚焦数学核心素养 设计单元—课时教学——以高中“一元二次函数、方程和不等式”单元为例［J］.数学通报，2021，60（06）：3035.

［6］徐强.基于“单元”视角，设计问题驱动——以“圆周角（第2课时）”教学设计为例［J］.数学教学通讯，2022（26）：1720.

基金项目：宁夏师范学院2023年度大学生科技创新基金项目

作者简介：曹雪芹（1998— ），女，汉族，山西大同人，硕士研究生，研究方向：學科教学（数学）；陈志恩（1977— ），男，汉族，宁夏固原人，硕士研究生，教授，硕士生导师，研究方向：数学教育，主持参与各级各类项目多项。