含参量积分函数的奇偶性
张清邦
(西南财经大学 数学学院,成都 611130)
0 引 言
第十三届全国大学生数学竞赛补赛试题的第二题:设
证明:在区间(-1,1)上,函数f(x)有且仅有两个实根.
这道题目引起了思考,由于区间(-1,1)是对称区间,能不能应用函数f(x)的奇偶性仅证明该函数在半区间(-1,0)或(0,1)上仅有一个实根?显然f(x)是含参量的积分函数.在《高等数学》和《数学分析》教材中,含参量积分函数的分析性质,如:连续性、可微性、可积性等,得到了深入分析.文献[1]给出了一类含参量积分函数的连续性及其应用.但对含参量积分函数的奇偶性鲜有讨论.另一方面,函数的奇偶性在积分运算中,可以简化定积分和重积分的运算.
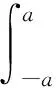
1 含参量积分函数的奇偶性
定义1设多元函数f(x1,x2,…,xn)在区域Ω有定义.
(i) 称f(x1,x2,…,xn)在Ω上是关于xi(i=1,2,…,n)的偶函数(或奇函数),若对任意(x1,x2,…,xn)∈Ω,都有(x1,…,xi-1,-xi,xi+1,…,xn)∈Ω且
f(x1,…,xi-1,-xi,xi+1,…,xn) =f(x1,…,xi,…,xn) (或-f(x1,…,xi,…,xn));
(ii) 称f(x1,x2,…,xn)在Ω上是偶函数(或奇函数),若对任意(x1,x2,…,xn)∈Ω,都有(-x1,…,-xn)∈Ω且
f(-x1,…,-xi,…,-xn)=f(x1,…,xi,…,xn) (或-f(x1,…,xi,…,xn)).


(i)f(x,y)在D上是关于x的偶(奇)函数;
(ii)f(x,y)在D上是偶(奇)函数.
证(i) 充分性:由函数奇偶性的定义及积分的线性运算性质易得.

(ii) 充分性.对任意x∈(-∞,+∞),当f(x,y)在D上是偶函数时,有f(-x,-y)=f(x,y),则


根据引理1可知,f(-x,-y)=f(x,y),故f(x,t)在D上是偶函数.
同理可证,f(x,t)在D上是奇函数等价于F(x)是奇函数.
定理2设二元函数f(x,y)为区域D=2上的连续函数,φ1(x) 和φ2(x)是(-∞,+∞)上的偶函数,则当f(x,y)在D上是关于x的奇(偶)函数时,G(x)=f(x,y)dy在(-∞,+∞)上是奇(偶)函数.
证当函数f(x,y)在D上是关于x的奇函数时,对任意给定的y∈,都有f(-x,y)=-f(x,y).故
所以G(x)在(-∞,+∞)上是奇函数.同理可得,G(x)在(-∞,+∞)上是偶函数.
如当x∈[-2,2]时,φ1(x)=x+2,φ2(x)=x2-6,f(x,y)=xy是关于x的奇函数,但
是非奇非偶函数.

定理3设二元函数f(x,y)为区域D=2上的连续函数,φ1(x)和φ2(x)是(-∞,+∞)上的奇函数.则当f(x,y)是D上的奇(偶)函数时,G(x)=f(x,y)dy是(-∞,+∞)上的偶(奇)函数.
证设φ1(x)和φ2(x)是奇函数,当函数f(x,y)在D上是奇函数时,对任意给定的(x,y)∈D,都有f(-x,-y)=-f(x,y).故
所以G(x)在(-∞,+∞)上是偶函数.
当函数f(x,y)在D上是偶函数时,对任意给定的(x,y)∈D,都有f(-x,-y)=f(x,y).故
所以G(x)在(-∞,+∞)上是奇函数.
定理4设二元函数f(x,y)为区域D=2上的连续函数,φ1(x)和φ2(x)是(-∞,+∞)上的偶函数且对任意x都有φ1(x)+φ2(x)=0,则当f(x,y)在D上是偶(奇)函数时,函数G(x)=f(x,y)dy在(-∞,+∞)是偶(奇)函数.
证设函数f(x,y)在D上是奇函数,则对任意(x,y)∈D,都有f(-x,-y)=-f(x,y).故
所以G(x)在(-∞,+∞)上是奇函数.同理可证,G(x)在(-∞,+∞)上是偶函数.
2 含参量积分函数的奇偶性的应用
本节中,将利用上节结论,先讨论含参变量积分函数的导数的奇偶性,然后给出第十三届全国大学生数学竞赛补赛第二题的解法.

证当f(x,y)在D上是关于x的奇函数时,由定理2可知,F(x)在[-a,a]上是奇函数.又由文献[4]可知,F(x)在[-a,a]上是可微的且
故对任意x∈[-a,a],都有
即F′(x)在[-a,a]上是偶函数.
同理可证,当f(x,y)在D上是关于x的偶函数时,F′(x)在[-a,a]上是奇函数.


对任意x∈[-a,a],由文献[4]可知,F(x)在[-a,a]上可微.又因
所以当f(x,y)在D上是偶函数时,可得
即F′(x)在[-a,a]上是奇函数.
当f(x,y)在D上是奇函数时,F(x)=0(∀x∈[-a,a]),由F(x)的可微性知F′(x)在[-a,a]上是偶函数.

证当f(x,y)在D上是关于x的奇函数时,由函数φ1,φ2的奇偶性及定理2可知G(x)在[-a,a]是奇函数.因为由文献[4-5]可知,函数G(x)在[-a,a]上可微,且满足
所以对任意x∈[-a,a]都有
G′(-x)=-(G(-x))′=-(-G(x))′=G′(x),
即G′(x)是[-a,a]上的偶函数.同理可知另一结论成立.

证由定理3,类似命题1的证明,易知结论成立.
接下来,利用定理1给出下列竞赛题的解答.

证令g(x,t)=|x-t|e-t2,易得g(x,t)在区域D=[-1,1]×[-1,1]上连续,且是D上的偶函数.由定理1知,函数f(x)是区间(-1,1)上的偶函数.下面证明f(x)是区间(0,1)上仅有一个实根.
对任意x∈(0,1),因为
所以
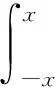


3 结 论
本文讨论了含参量积分函数的奇偶性,然后利用所得结果讨论了含参变量积分函数的导数的奇偶性,并给出第十三届全国大学生数学竞赛补赛第二题的解答.
致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.

