职业本科计算机专业离散数学课教学改革初探

王 礼

(广西城市职业大学 信息工程学院,广西 崇左 532200)

0 引 言

2019年,教育部批准通过了一批全国职业本科试点高校.广西城市职业大学成为全国首批、广西第一所职业本科试点高校,并且一直在积极探索职业本科教育的恰当模式.职业本科目前在国内属于教育界的新生事物,但传统的课堂理论教学依然是其核心环节之一,因此职业本科教师必须积极探索适合职业本科教育的理论教学模式.

笔者在广西城市职业大学信息工程学院为“大数据技术与应用”专业讲授离散数学课的过程中,经过教学实践与探索,愈发认识到将它与计算机其他课程紧密联系起来的重要性.

计算机的发展与离散数学的主要内容如数理逻辑、集合论、数论、抽象代数和图论等有非常密切的联系,可以说计算机离不开离散数学,离散数学在计算机相关专业中有着特别重要的作用[1].离散数学被看做计算机的数学,是计算机类各专业的核心基础课程,也是计算机类专业许多核心课程(如数据结构、编译原理、数据库原理、人工智能等)的先导课程[2].现代电子计算机的核心理论基于布尔代数,它属于离散数学.因此,离散数学在计算机学科中居于核心位置.

文献[3]研究发现,传统的离散数学教学将理论学习与计算机实践相互割裂,降低学生学习效率和影响教学质量,并提出应与计算机知识结合起来.文献[4]提出在离散数学的教学过程中加入实践性内容,通过将理论知识应用到程序设计中来深化学习.

学生对离散数学的学习将直接决定其计算机基础理论水平.尤其对于职业本科,当前迫切需要探索出一套合理的离散数学教学模式.本文主要从“知识串联”的角度,来积极进行实践与探索.从我校计算机应用工程专业与大数据技术与应用专业的人才培养方案可知,将职业本科学生培养为高级技能型人才,是最终的培养目标.文献[5]提出职业本科重技术、重实践,应更新教学内容,改革教学方法和手段,支撑职业本科学科与专业同步高质量发展.人才培养紧密围绕学生实践能力的提高,理论最终为了实践,这就要求知识的传授务必要理论结合实际.

为了有效开展教学工作,需要先掌握职业本科特点、职业本科学生特点、离散数学课程特点,具体总结见表1.

表1 职业本科及相关要素的特点

通过观察表1,会发现突出矛盾:一方面,离散数学课理论性强,复杂抽象,但很重要;另一方面,学生接收能力弱,课时少.

为了解决矛盾,达到职业本科育人目的,在制度允许框架内尽可能改革是大势所趋.笔者经过探索总结出一套离散数学课教学模式.该模式由教材选择、知识串联、实例设置、考核标准四个部分构成,如图1所示.

图1 教学模式流程图

1 教学实践与探索

1.1 教材选择

教材的选择很重要.好的教材,使用起来事半功倍,教师教学轻松、学生学有所获.而教材的选择需考虑较多因素,如人才培养方向、学科、专业、课时等,但当前还未出现与职业本科配套的离散数学教材.为稳妥起见,笔者所在学校选择了普通本科所用的、得到广泛认可的清华大学出版社出版的离散数学教材[6].

1.2 知识串联

离散数学的理论体系繁杂而庞大,若孤立地讲授,学生难以理解.职业本科的一条重要理念是理论要与实践结合,即是将理论知识推广和应用.因此,首先需要找出离散数学课与其他课程内容的交集.从人才培养方案来看,计算机应用工程专业和大数据技术与应用专业包含多门专业基础课,其中与离散数学内容存在交集的有:C程序设计、数据结构、计算机网络、数据库、编译原理、计算机组成原理等,如图2所示.

图2 与离散数学存在交集的计算机专业课程

接下来,需要找出离散数学跟这些课程的交集,将离散数学理论知识与这些课程中的相关知识串联起来,打通课程边界.这样一方面可加强学生对基础的数学理论的理解,另一方面可提高学生的实践水平,从而体现出职业本科内涵.

离散数学部分理论与其他课程内容的关联详情见表2.

表2 离散数学部分理论与计算机专业课程知识关联表

从表2可以看出离散数学课的核心地位,它与其他基础课或多或少存在一定关联.由于职业本科的理论课时少,所以有必要根据它与其他课程内容的关联程度,以及实用价值,在授课时对教材内容适当删减,并对特定的知识内容进行扩充,即增加实例.

1.3 知识串联方法与实例设置

“知识串联”,是将离散数学理论知识与计算机专业其他课程知识串联融合.讲课时,先讲解理论,再讲与该理论关联的其他课程知识.学生从而能更好地理解理论,也更容易理解其他课程相关知识.如果学生暂未学习到相关的课程知识,则先花几分钟讲解以作衔接.“实例设置”,是举例说明理论在实际中的应用,化抽象为形象.下面通过一个例子来说明.

离散数学第三章讲数理逻辑,它与计算机组成原理中的CPU直接相关.这个逻辑和顺序是:复合命题—>表达式—>真值表—>逻辑门—>晶体管—>半加器、全加器—>CPU.讲课时需要层层递进,循循善诱,一步步引导学生,见表3.

表3 离散数学复合命题与计算机组成原理知识串联和实例设置举例

在讲课中,从基础理论,一步步引申出实际应用,化抽象为形象,充分调动了学生的学习热情.在理论中插入实例,在实例中反思理论,以此完成理论到实践的完美过渡.最后顺利融入了课程思政,最终将传授知识和思政育人有机融合,一举多得.

课后作业是让学生画出几种基本的逻辑门及对应的真值表,以及设计出半加器、全加器.

在整个过程中,学生懂得了“复合命题”“表达式”“真值表”“成真赋值”“成假赋值”“连结词完备集”,以及它们与计算机组成原理中的逻辑门、半加器和全加器的关系,进而初步理解CPU并非神秘事物.

将离散数学中数理逻辑知识与计算机组成原理课程知识串联,是具有代表性的一个案例,也是本课程改革的一个缩影.

1.4 考核标准

期末总评由“平时”和“期末”组成.平时占40%,包括出勤次数、课堂表现、平时作业质量等.平时作业如有明显雷同,酌情扣分;期末,即期末考试的卷面分,在总评中占60%.考核标准最大的特点在于:作业题与考试题的考察范围不只是单一的离散数学理论知识,而更多是将这些理论同其他课程中的相关知识串联起来.这就要求学生务必将离散数学相关理论与其他课程中的相关知识结合起来学习,形成知识串联与课程融合的观念,从而能更好地理解和运用离散数学理论知识.

2 教学效果

笔者对2019级本科大数据技术与应用专业离散数学课的教学运用了本教学模式,平时已经取得较好的反响.为了真正验证本教学模式的效果,对6个班(共238人),发放了问卷调查,得出结果见表4.

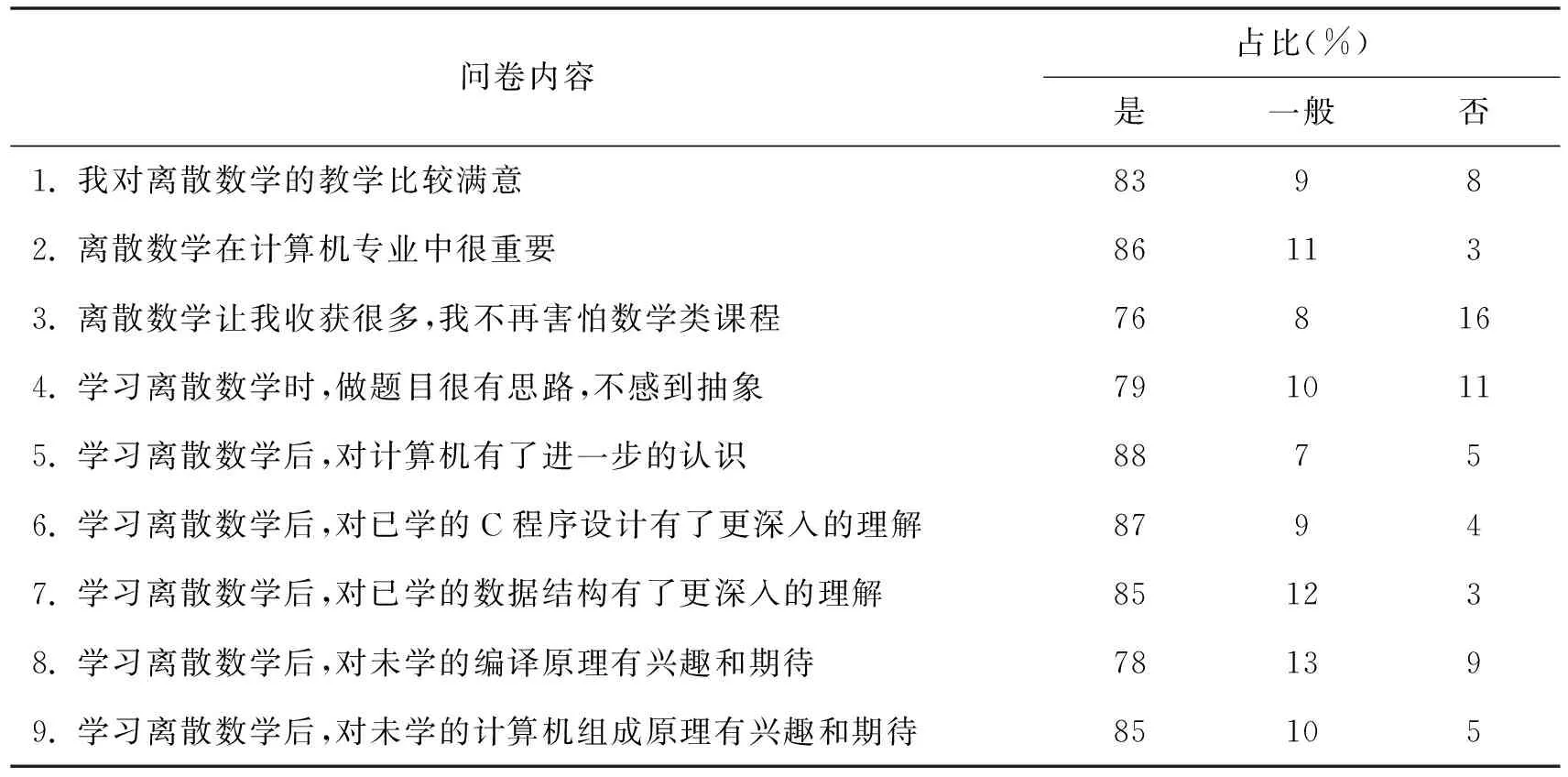
表4 问卷调查结果统计

由表4可知,在这种教学模式下,83%的学生对离散数学课教学比较满意;离散数学的学习让76%的学生收获多,不再害怕数学类课程;通过学习离散数学,大多数学生对以往的专业课知识有了进一步的理解,同时对未来要学的专业课程有了兴趣和期待.总之,将离散数学与各专业课串联起来,极大激发了学生的学习积极性.

3 结 论

本文提出了一种职业本科离散数学课的教学模式,核心是在离散数学课的教学中,将离散数学知识与计算机其他课程知识串联起来,让学生对离散数学的理论知识不再感到抽象和晦涩.这种知识串联的教学方式,一定程度上破除了传统离散数学教学中理论知识孤立无用的弊端.它提升了学生的学习积极性、理论水平和实践能力,从而为职业本科计算机专业离散数学课的教学找到了一条出路.

致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.