生物入侵诱导下的集群网络结构

陈晓薇, 苏 敏

(合肥工业大学 数学学院,合肥 230601)

0 引 言

物种如何集群成群落是群落生态学中的一个重要问题[1].很少在自然群落中观察到稳定的群落组成,生物入侵被认为是群落集群的重要方式之一[3].一般来说,群落集群是不可预测的,其集群的顺序、本地群落大小的微小变化或者不同的入侵时间都可能会导致完全不同的群落结构[4].为了回避这些困难,生态学家们将群落集群过程建模为物种按照一定的规则从物种池入侵到本地群落的过程,以研究群落的集群过程[5].

有关群落集群的研究主要分为两个内容:

① 生物入侵对于本地群落的影响; ② 成功入侵群落的续存物种特征分布,分析群落中续存物种能够入侵成功的原因[7].针对第一个内容的研究表明,物种的不断引入和灭绝会导致本地群落物种丰富度和网络结构的变化.物种入侵是否对本地的生物多样性构成巨大威胁一直存在争议[8].一些研究结果表明,入侵会减少本地群落的生物多样性、种群丰度以及生态系统功能[9].但是在某些情况下,外来物种也可以通过促进作用增加本地物种数量,或者不会产生重大影响.对于第二个研究内容,外来物种能否成功入侵受多种因素影响,反映入侵物种与其本地群落之间相互作用的变量(如营养级水平)、基本的物种特征(如摄食范围的中心以及生态位宽度),或网络的拓扑结构都能影响物种是否能够入侵成功[11].

随着新物种的引入和群落中已有物种的灭绝,这意味着建模中一次性确定的群落不能够完全代表自然群落,自然界中的群落形成更倾向于集群的方式[13].然而,大多数研究仅通过对比入侵前后群落的变化,考虑入侵对于本地群落的影响,对于生物入侵构成的集群群落和非集群群落的区别的了解仍然缺乏.本文建立了基于特征的食物网动态模型,利用生态位模型生成了物种池,根据不同聚集方式构建了以下两种网络:

①将物种池中所有的物种同时引入环境中,从而获得非集群网络;②从物种池中随机选取基础物种构建初始网络,剩余物种池中物种对其进行随机入侵获得集群网络.

首先对比了最终网络的特征和度的分布,然后计算了网络结构指标,探究了物种丰富度与网络拓扑结构之间的关系.研究发现,虽然两类网络的物种丰富度与其他指标的关系相似,但集群网络的续存物种分布更具有规律性,二者的网络结构也并不相同.因此,一次性确定的网络和生物入侵构成的集群网络不具有等效性.

1 模型建立

本文构建了一个基于物种生态位特征的食物网动态模型[13],模型假设物种的生态位特征(例如,体型大小)能够影响物种的生长率[15],以及物种之间的捕食相互作用关系[1].同时,模型假设群落中的物种存在种内竞争作用,为了简化模型,忽略了种间竞争;考虑了物种间存在捕食互作关系,两物种是否互作依赖于生态网络的相互作用矩阵{aij},当物种j捕食物种i时,aij=1,否则为0.捕食采用Holling II的功能反应,如果捕食者的每个猎物在被捕食后都为其提供不同的营养,则相互作用强度仅在该猎物的密度中饱和[13].基于以上假设,给出了群落动态的微分动力模型:

(1)

其中,Hi(i=1,…,S)是物种i的个体数量,参数ri是自然增长率,δi是密度依赖的自身生长制约,di是自然死亡率.φij,x(i≠j,x=+,-)为敌对的相互作用强度,半饱合常数为h.E+指的是物种i所消费的食饵资源集合,而E-指的是网络中能够捕食和消费物种i的所有物种集合.为了简化模型,更好的探究生物入侵对于食物网结构的影响,假设参数δi和di均是常数.

虽然在先前的许多研究中,常常会假设宿主的自然增长率ri为常数.但结合相关实验数据,发现自然增长率很可能会随着物种生态位特征(如体型大小)的增加而减小[15].因此,本文假设物种的自然增长率ri与其生态位特征xi有关,服从高斯函数:

(2)

其中,σr代表增长率的分布宽度,r0为最大自然增长率.

其次,本文假设物种捕食猎物所获得的能量以一定概率转化为其自身的增长.即成对的敌对系数满足φij,+=ε·φij,-,(0<ε<1),其中φij,+为物种i作为捕食者时的捕食正作用,φij,-为物种i作为猎物时的捕食负作用,ε为转化概率.使用高斯函数来描述捕食相互作用的强度:

其中,α0为捕食强度的最大值,xi为物种i的生态位值,μp是物种i与j之间的最优性状差,σp代表捕食互作的范围或宽度,数值越大则捕食物种具有更宽的食饵资源,说明该捕食者更具泛化性.

2 数值模拟与分析方法

2.1 食物网生成方法

基于生态位模型,依据物种数量(S)和网络连接(C=L/S2)作为输入参数生成了200个带有相互作用关系的物种池[17].首先,将物种安排在一个一维的“生态位数轴”中,再以分层的方式将捕食者和猎物链接分配给网络中的每个物种,从而成功生成逼近现实世界食物网的生态网络.在网络中,每个物种被随机分配了服从[0,1]间的均匀分布的生态位特征值xi,结合(2)和(3)可以计算出每个物种的自然增长率和物种间的捕食作用强度.生态网络生成以及模型中所用到的参数定义与取值参见表1.

表1 模型中参数定义与取值范围

2.2 数值模拟

研究了非集群和集群两类网络.对于非集群网络,考虑物种池中所有的物种,采用龙格库塔方法对方程(1)进行3000步数值模拟,使得网络达到平衡.在平衡时刻,剔除种群大小低于灭绝阈值(<10-3)的物种.

对于集群网络,首先,从物种池中随机选取n0个物种构成初始食物网,并将它们从物种池中移出.同样,采用龙格库塔方法对方程(1)进行3000步数值模拟,获得平衡的初始网络.其次,从物种池中选择物种对当前的稳定群落进行入侵,每个入侵物种都依次从物种池中随机选择且被选择后即从物种池中删除.每次仅引入一个物种,物种入侵后都进行了200步的群落动态模拟,直到物种数量达到平衡.在每次种群动态模拟结束后,种群大小低于灭绝阈值(<10-3)的物种会被移除群落.重复上述过程,直到物种池子内所有的物种都被选择一次,然后得到稳定的食物网结构,此时群落的物种丰富度和总生物量趋于稳定.结果显示,所有200个群落在经历750次入侵之后均可获得最终稳定网络.

2.3 网络分析

3 主要结果

3.1 稳定网络的物种共存情况

通过上述群落动态的数值模拟,结果显示,生物入侵影响稳定网络中的物种续存,尤其对优势种有着显著影响(图1).通过对比非集群网络(图1a)和集群网络续存物种的生态位分布情况(图1b),发现续存物种的生态位都在两端时频率最高,其中非集群网络的物种在生态位值为0的邻域内更多,集群网络的则在生态位值为1的邻域内更多.通过对比非集群网络和集群网络中优势种的生态位分布情况,发现非集群网络的优势种占据整个生态位(生态位范围:[0,1]),但其分布模式的随机性比较强(图1c);而集群网络的优势种仅出现在生态位较小的位置(生态位范围:[0,0.5]),其频率随着生态位的增加而下降,分布函数更接近于幂律分布(图1d).

图1 续存物种及优势种的生态位频率分布

3.2 续存物种的度分布

模拟结果显示,集群能够显著影响续存网络中物种的度分布(图2).非集群网络中续存物种的度分布呈双峰形式(图2a);随着物种的出度增加其频率降低,其中在出度较大时频率下降更为明显(图2b);类似地,随着入度的增加续存物种减少(图2c).与非集群网络相比,集群网络中物种的度分布更具有规律性.频率分布的拟合函数显示,集群网络中续存物种的度分布服从正态分布(图2d);网络中物种的出度和入度也均随着其度值的增加而频率降低.其中,物种的出度的频率分布接近正态分布(图2e),入度的频率分布接近幂律分布且其下降速度更为显著(图2f).对比两种网络,发现集群网络中出度和入度在较小值的频率更高,随着出度和入度的增加,其频率的下降速率也更为显著(对比图2b和图2e;对比图2c和2f).

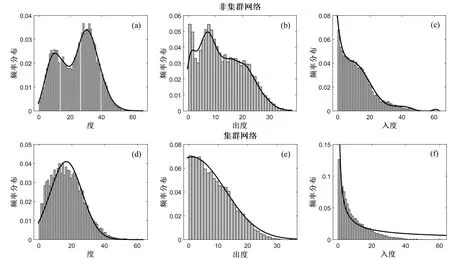
图2 续存物种的度分布

3.3 网络结构及食物网特性

先计算了上述物种网络指标和食物网特性,研究结果表明,集群对网络的结构属性有着显著影响.图3显示非集群网络的物种丰富度略大于集群网络中的丰富度,换言之,生物入侵情况下不能共存的物种可能在非集群网络中可以共存.集群网络的群落生物量明显大于非集群网络(图3a),但非集群网络的连接度高于集群网络(图3b);嵌套发生在专食性物种倾向于与更多泛化物种相互作用的物种的适当子集相互作用时,两类网络的嵌套程度相似,非集群网络的嵌套程度略大于集群网络(图3c);相反地,集群网络的模块性高于非集群网络,具体来说,集群网络的网络划分更加明显(图3d);非集群网络的一般性和脆弱性大于集群网络(图3e,3f);非集群网络的营养相似性高于集群网络,即非集群网络中的续存物种共享更多的猎物(图3g).

图3 网络指标和食物网特性对物种丰富度变化的响应

进一步分析了网络结构指标与物种丰富度之间的关系.在两种网络中,物种丰富度都与群落生物量呈显著正相关(p<0.001;图3a),且在集群网络中的正相关性更强;丰富度与连接度呈负相关(p<0.01,图3b),但随着非集群网络物种多样性的增加,其连接度的下降速度比集群网络更快;网络的嵌套程度随物种丰富度的增加而降低(图3c);相反地,物种丰富度导致网络的模块性增加,但对两个网络都不显著(p>0.1;图3d).两种网络的物种丰富度都与食物网的一般性之间无显著相关性(p>0.1;图3e);集群网络的物种丰富度与脆弱性正相关关系显著(p<0.001),在非集群网络中呈负相关,但不显著(p>0.05;图3f);在两种网络中,营养相似性都随物种丰富度的增加而增加,但都不显著(p>0.05;图3g).

4 结 论

集群网络的拓扑结构是生态学研究的重要问题之一,人们常通过生物入侵的建模来研究自然群落的集群问题.本文旨在进一步探究非集群群落和集群群落是否也具有一定的等效性.首先探讨了集群和非集群网络中续存物种的特征及度分布情况.研究发现,两种网络的续存物种都在两端时频率最高.通过分析生态位模型的生成规律,结果显示生态位特征值更大的物种更不易被捕食;同时,根据经验网络数据和模型设定,生态位值更小的物种其自然增长率更大,因此生态位处于两端的物种更易续存.进一步对比优势种的续存情况,不难发现集群网络的优势种都处于生态位特征值较低处,符合经验网络中生态位及自然增长率间的负相关规律.类似地,集群网络的度分布也比非集群网络更具有规律性,物种度和出度的分布服从正态分布而入度服从幂律分布更符合自然群落中营养级物种的分布情况.集群也对网络结构属性产生重要影响,集群促使饱和网络的物种丰富度降低,意味着生物入侵情况下不能共存的物种可能在非集群网络中可以共存.最后,本文探究了物种丰富度对于网络结构的影响,发现两类网络的物种丰富度与其他网络指标的关系基本相似,集群只对网络脆弱性与丰富度之间的正负关系发生逆转.综上,本文的结果丰富了群落构建的模型研究,发展了集群网络的相关理论.

致谢作者非常感谢杂志编委以及审稿专家提出的宝贵意见.