分离变量法求解一些非线性发展方程的显式解

王凡凡, 江志松

(华东理工大学 数学学院,上海 200237)

0 引 言

数学物理方程[1]是大学数学中重要的学习内容,关于线性偏微分方程的求解吸引了一些大学数学工作者的关注和研究[2-3].在求解线性偏微分方程的方法中,分离变量法是最有效的一个方法.文献[4]用分离变量法研究了无界域内线性拉普拉斯方程的解.然而,由于方程的非线性,在试图将分离变量法推广到求解非线性偏微分方程时往往会遇到极大困难.

本文的目的是将分离变量法应用于求解一些非线性发展方程,并讨论求解过程中用到的技巧和方法.基于对非线性发展方程结构的观察,利用分离变量法成功得到了Harry-Dym方程,Hunter-Saxton方程,非线性扩散方程,半经典极限KdV方程等若干非线性发展方程的新的显式解析解.

方便起见,在本文中,如果无特别声明,ci(i=1,2,3,…)均表示常数.

1 Harry-Dym方程

Harry-Dym方程具有如下形式[5]

(1)

(2)

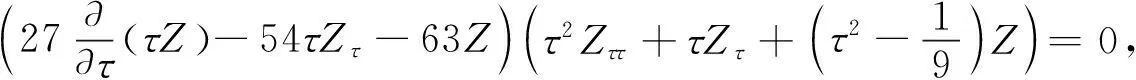
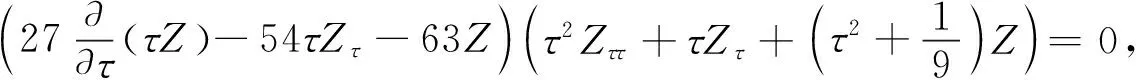
从而,有

与

(3)

分别给出方程(2)和(1)的解.从方程(3)可知,当c1与c2互为相反数时,ut在有限的时间内会出现爆破现象.在文献[5]中,Wadati得到的尖角解也具有这样的性质,即一阶导数为无穷.

2 广义的Harry-Dym方程

考虑如下广义的Harry-Dym方程[6]

(4)

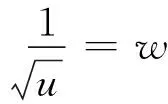
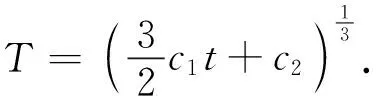
方便起见,考虑

(5)

方程(5)具有参数形式的解

(6)

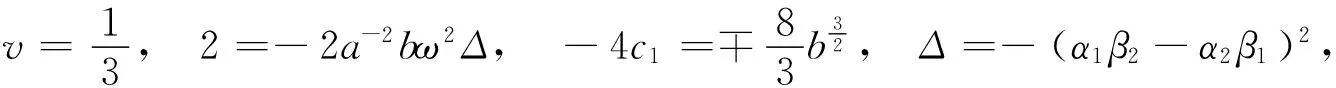
Zv=α1Uv+α2Vv,Mv=β1Uv+β2Vv,Fv=τZ′v+vZv,Gv=τM′v+vMv,

N=ZvMv,N1=ZvGv+MvFv.

3 Hunter-Saxton方程

Hunter-Saxton方程

utxx+2uxuxx+uuxxx=0.

(7)

描述向列型液晶中波的传播[7].假设u(x,t)=X(x)T(t)并代入(7),可得

(8)

(9)

(i) 若c3=0,有

(10)

即有如下方程

当取符号为负时,类似得到

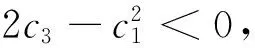
4 Cao-Geng提出的可积方程[8]

(11)

假设u(x,t)=T(t)X(x)并代入方程(11),有

(12)

(13)

(14)

(15)

注意到方程(15)的第二个方程通过换元τ→-τ可以变成第一个方程.而(15)关于P1的第一个方程是第二类Painlevé方程中常数为零时的标准形式.这个方程的解是τ的单值函数,在动极点τp附近可以用如下级数表示

其中m=±1,τp和C是任意常数,bn(n≥6)由τp和C唯一确定.从方程(14)可以给出方程(12)中第二个方程参数形式的解

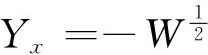
5 非线性扩散方程

非线性扩散方程

ut+(u-2ux)x=0

(16)

在等离子、固态物理等其他领域如冶金学、聚合物科学都有重要的应用.现寻求其分离变量形式的解,将u(x,t)=T(t)X(x)代入方程(16),有TtT=c1,XXxx=c1.求得

容易发现当常数c1与c2互为相反数时,ut(x,t)在有限时间范围内出现爆破现象.

6 半经典极限KdV方程[9]

(17)

将u(x,t)=T(t)X(x)代入方程(17),可以得到分离变量形式的解

半经典极限KdV方程有两个重要的特殊形式:

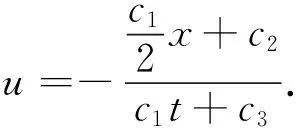
7 结 论

本文讨论了分离变量法在求解非线性发展方程中的几个例子,用该经典的方法求解了Harry-Dym方程,Hunter-Saxton方程,非线性扩散方程,半经典极限KdV方程等方程的新的显式解析解,介绍了求解过程中用到的技巧和方法.本文研究说明,通过对非线性发展方程结构的观察,利用一些技巧,可以利用分离变量法求解一些非线性发展方程.

致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.