高等几何中无穷远元素在虚拟仿真实验课程中的应用

赵 越, 邓修营

(云南大学 数学与统计学院,昆明 650000)

0 引 言

无穷远元素是高等几何课程中的重要内容,是联系初等几何和高等几何的一条纽带,它的引入使得高等几何具有显著的独立性,对培养学生解决问题以及抽象性思维的能力具有重要作用.在高等几何课程的教学过程中,目前存在的问题是学生习惯于停留在欧氏几何的具象思维上想象无穷远元素,难以建立对无穷远元素的抽象思维[1].为了学生能够尽快的从初等几何中的欧氏空间进入到高等几何中的仿射空间、射影空间,那么对无穷远元素的深入理解就起着至关重要的作用.为明确起见,现将无穷远元素相关定义摘录如下:

定义1[2]在平面内对于任何一组平行线引入唯一一点,叫做无穷远点,此点在组中每一直线上而不在此组之外的任何直线上,无穷远点记作P∞.

定义2[2]一平面内一切无穷远点的集合组成一条直线,称为无穷远直线,记作l∞.

定义3[2]空间里的一切无穷远点的集合组成一个平面,称为无穷远平面π∞.

定义4[2]无穷远点,无穷远直线和无穷远平面统称无穷远元素.

定义5[3]圆环点为圆与无穷远直线的交点,即共轭复点矩阵形式I[1i0]和J[1 -i0]称为圆环点.

为适应教学需求,辅助学生更好的理解无穷远元素,同时响应《中国制造2025》国家行动纲领,根据虚拟仿真实验教学一流本科课程建设需要(下称虚拟仿真实验课程),按照“虚实结合,以需补实”的创新性原则,实现了“理论、虚拟仿真、实际操作一体化”的新型教学方式.在此实验课程中,通过计算机视觉中摄像机内参数求解,也称之为摄像机标定这个技术应用,使得无穷远元素从抽象转化为具体.利用无穷远元素对摄像机内参数矩阵K的约束进行求解是目前一种重要方法[3].学生通过此实验课程可以建立对无穷远元素的直观认识.无穷远元素在虚拟仿真实验课程中是如何应用的,对于高等几何的教学有重要的参照意义,本文对此做一些讨论.

1 无穷远元素与虚拟仿真实验原理的联系

虚拟仿真实验课程以高等几何的基本概念为基础并结合了其他学科研究成果,其核心原理来自于一种利用正三棱柱靶标求解摄像机内参数的方法[4]与利用三个相切圆线性求解摄像机内参数[5],学生通过学习此实验课程能够对高等几何中的无穷远直线和圆环点的概念有更直观的认识.

利用正三棱柱靶标求解摄像机内参数的方法中的标定模板是正三棱柱,如图1(a)所示,利用三个相切圆线性求解摄像机内参数中的标定模板是三个相切圆,如图1(b)所示.

图1 (a)正三棱柱标定模板和(b)三个相切圆标定模板

1.1 无穷远元素在利用正三棱柱靶标求解摄像机内参数中的应用

通过以下命题和推论体现无穷远元素在利用正三棱柱靶标求解摄像机内参数中的应用.

命题1已知图1(a)中1幅正三棱柱ABC-A1B1C1的几何体的像,则

(i) 可求得6组正交方向消失点(无穷远点的像)的坐标;

(ii) 可求得3组圆环点的像的坐标.

证设三角形ABC中的线段AD,BF,BC,AC所在直线的无穷远点矩阵形式分别为P1∞,P2∞,P3∞,P4∞,它们对应的像点矩阵形式分别为p1,p2,p3,p4.O分别是AD,BF的中点,D,F分别是BC,AC的中点.

(i) 在成像中,A,B,C,D,O,F的对应点坐标分别为Am,Bm,Cm,Dm,Om,Fm.根据高等几何中调和共轭理论[2],易得一条线段被它的中点和这条直线上的无穷远点调和分离.因为在正三棱柱中O分别是AD,BF的中点,D,F分别是BC,AC的中点,所以

(1)

根据射影理论,变换点线结合性和交比不变性,(1)式转化为

(2)

因为AD⊥BC,BF⊥AC,像平面上两组正交方向消失点分别为p1,p3和p2,p4.同理可分别在正方形ACC1A1和正方形BCB1C1所在平面的成像上求得两组正交方向消失点和.

(ii) 设三角形ABC所在成像平面上的圆环点的像的坐标矩阵形式为mi1[x1+x2iy1+y2i1],mj1[x1-x2iy1-y2i1].因为AD⊥BC,BF⊥AC,同理(i)求得两组正交方向消失点分别为p1,p3和p2,p4.根据调和共轭理论[3],得到关于圆环点的像的坐标的方程

(3)

通过(3)式可以求出三角形ABC所在成像平面上的圆环点的像点坐标.同理可得两正方形ACA1C1和BCB1C1平面上的圆环点的像的坐标.

推论1已知图1(a)中1幅正三棱柱ABC-A1B1C1的像,可获得3个不同平面上的消失线(无穷远直线的像).

显然命题1(i)求得的6组正交方向消失点,每组两两相连即得6条消失线,即获得3个不同平面上的消失线,证明略.

1.2 无穷远元素在利用三个相切圆求解摄像机内参数中的应用

以下命题和推论体现无穷远元素在结合三个相切圆求解摄像机内参数中的应用.

命题2已知图1(b)中1幅包含三个相切圆Qi(i=1,2,3)平面的像,可求得1组该平面正交方向消失点的坐标.

证根据三相切圆标定板图像的特征点坐标,利用最小二乘法拟合各个圆的成像曲线,得到各条曲线方程,即圆Qi的像Ci(i=1,2,3)的方程.由于三个相切圆Qi(i=1,2,3)有不同的圆心(不共线),在单应矩阵H的作用下[8],得到圆与其像的关系

Ci=H-TQiH-1(i=1,2,3),

其中圆Qi和其像Ci分别表示方程的系数矩阵.考虑两个线性组合

这是一个关于β的一个三次方程,有三个根.通过方程

解得

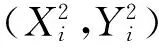
它表示通过圆心的像的直线,其中oi表示圆Qi圆心的像坐标矩阵形式,即过圆心的像的直线lij=oi×oj是Δj的特征值β1对应的广义特征向量,从而可求出圆Qi的圆心的像的坐标oi.计算出oi的坐标并检测出Q1和Q3的切点A的像的坐标mA,进而可以计算出mA关于圆心的像o1在曲线C1的对应点mD,如图2.故mA,o1,mD所在的直线是圆Qi上一条直径的像,由调和共轭和交比不变性可得(mAmD,o1v1)=-1,从而解得该直径方向上的一个消失点v1.然后计算mA,mD关于曲线C1的切线l1,l2,则可求解出两切线方向上的一个消失点v2.并且由于在空间的同一个平面上,圆直径两端点的切线和直径是垂直的,所以在图像上v1,v2是一组正交方向上的消失点.

图2 mA与mD是一对对应点

推论2已知图1(b)中的1幅三相切圆Qi(i=1,2,3)的像,可获得其所在平面的消失线.

根据命题2获得一组正交方向上的消失点,连线即是三相切圆所在成像平面的消失线,证明略.

由于p1,p3是一组正交方向消失点,根据成像原理可以得到

并且摄像机光心与消失点的连线方向与无穷远点的坐标矢量方向一致,即光心o与p1的连线op1和o与p3的连线op3相互垂直.因为外参数矩阵R,t分别是旋转矩阵和平移向量,具有正交性,所以可以得到方程[6]

(4)

注意到p2,p4也是一组正交方向消失点,因此可以得到

(5)

K-TK-1是一个对称矩阵,包含六个未知量,所以利用正交方向消失点对摄像机内参数矩阵K的约束,获取6组以上正交方向消失点,根据公式(4)和(5)即可线性求解摄像机的内参数.

从3幅以上图像获得互不平行三个平面上的圆环点的像之后,就可以求解摄像机内参数,获得内参数矩阵后,相应的旋转矩阵R和平移向量t即可求出[9].

2 无穷远元素在虚拟仿真实验课程中的体现

在高等几何课上,学生能学习到平行直线交于无穷远点,圆与无穷远直线交于两个圆环点.但是在日常生活中,并不会看到两条平行线的交点,更不要说圆与无穷远直线的交点了,这就为高等几何的教学带来了困难.学生带着习惯的具像思维来学习十分抽象的无穷远元素,导致很难完全理解无穷远元素且激发不起学生对于数学学习的兴趣.同时,数学原理与实际应用场景结合的案例很难在课堂上生动展示,无法满足理论联系实际的教学目的[8].而该虚拟仿真实验课程生动展示了无穷远元素在解决实际问题中的应用,有效辅助学生理解和掌握无穷远元素,提高了学生利用数学原理来解决实际问题的能力.目前,多数学生都有笔记本电脑、智能手机,在虚拟仿真实验系统[10]中学习更能激发他们的学习兴趣,提升他们的学习热情.

2.1 利用正三棱柱标定模板在虚拟仿真实验系统中进行标定

现实场景中的两条平行直线在像中会交于一点,这个点就是消失点.在虚拟仿真实验系统环境中,放置在实验桌上的正三棱柱靶标在摄像机下的像会在实验桌上的屏幕实时显示,如图3(a).从屏幕中的图像上可以看到,在场景中正三棱柱靶标的一个侧面的上下边是平行的,但在图像中却明显会交于一点.学生通过学习利用正三棱柱标定摄像机的原理以及操作仿真实验系统[10]能够对无穷远元素形成直观的认识.在该实验中,通过从不同方向对正三棱柱靶标拍摄获取照片即可进行摄像机标定.同消失点在虚拟仿真实验系统中的应用类似,通过正三棱柱靶标的像,可以获得圆环点的像,从而利用圆环点的像对摄像机内参数矩阵K的约束进行摄像机标定.

图3 虚拟场景中(a)正三棱柱靶标和(b)相切圆

2.2 利用三相切圆标定模板在虚拟仿真实验系统中进行标定

在系统中[10],学生可以通过移动摄像机得到三相切圆的清晰图像,三相切圆的清晰图像在屏幕上的显示,如图3(b)所示.如1.2的描述,在拟合三个相切圆的像之后,可以通过调和共轭以及交比不变性计算得到两正交方向的消失点,利用消失点对摄像机内参数矩阵K的约束求解得到摄像机内参数.

学生通过该虚拟实验仿真系统操作摄像机标定之后,能够切实的理解无穷远元素在现实生活中的具体应用,这恰好迎合了学生学习无穷远元素时的具象思维,有利于激发学生学习数学的兴趣,对高等几何的教学具有重要参照意义.

2.3 虚拟仿真实验系统中的四个应用

学生在完成系统中的标定模块后将进入到综合实验模块.在综合实验模块有四个基于摄像机标定的机械臂的工业应用,分别是形状识别、颜色识别、传送带视觉跟踪、无人饮料机售卖[10].学生可以自由选择感兴趣的应用,通过摄像头获取目标物体的图像,利用图像识别和检测算法得到物体在像素坐标系下的坐标.通过标定将物体的像素坐标系变换到机械臂坐标系下.在完成坐标转换的基础上,以机械臂为载体智能地完成对不同形状、颜色及运动状态的物体进行抓取和放置等操作,如图4所示.学生通过综合实验模块将进一步体会到无穷远元素在实际中的应用,同时加强自身的科学素养以及对计算机视觉等人工智能前沿技术的认识.

图4 四个机械臂应用虚拟场景

3 结 论

无穷远元素是高等几何中的重要内容,是联系初等几何和高等几何的一条纽带,同时也是教学中的难点.本文分析了无穷远元素是如何应用的,以及其在虚拟仿真实验课程中的体现,并给出在虚拟仿真实验系统中现实场景中的四个应用.通过分析无穷远元素在虚拟仿真实验课程中的应用,更好地把握抽象的数学概念,启发了学生的学习兴趣,对于高等几何的教学有重要参照意义.

致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.