数形结合思想在初中数学解题中的应用

王磊

【摘 要】  数形结合思想是数学领域非常重要的解题思想之一，在初中数学解题中，数形结合思想的应用，能够让一些原本复杂、较难解答的习题得以轻松解答，同时也能够培养学生的思维灵活性.因此，探索数形结合思想在初中数学解题中的应用，有着非常积极的研究价值.全文主要围绕“以数解形”“以形助数”两个方面分析数形结合思想的具体应用，抛砖引玉，希望能有一定参考价值.

【关键词】  初中数学；数形结合思想；解题教学

1  数形结合内涵与价值

在数学领域中，“数”与“形”是两个重要的因素，两者相互呼应，彼此转化，“数”即数字与数理关系，“形”即形状与图形变化，“数”具有规则性，“形”具有直观性，将数与形象结合，通过“数”与“形”之间的互通、转化，来剖析某一个数学问题[1].

在初中数学解题中，数形结合思想的应用主要有两种模式，一种是“以数解形”，一种是“以形助数”.“以数解形”指的是面对抽象的、复杂的图形，运用数字去定义图形，用数理关系去映射图形的特点，在运用数学方法去进行数算，解开数字及数理关系，也就解答了图形的特点.“以形助数”，则是面临繁杂的数字或数理关系，用直观的图像将其呈现出来，很多时候“一图胜千字”，可直观观察出图像的特点，进而对数理关系进行解答[2].

在初中数学教学中教导学生数形结合思想，能够提升学生的解题能力，使得学生面临繁杂的习题时，能够运用简便的方法去进行解答[3].同时，教师教导学生数形结合思想，还能够锻炼学生思维灵活性，引导学生从数与形两个方面，运用多种方法去解答习题[4].

2  数形结合思想的应用策略

2.1  以数解形

对于一些复杂的图形，用肉眼难以去观察到图形的规律，那么这个时候用数字去定义图形，再去解答代数，找到数理关系的规律，也就找到了图形的规律[5].

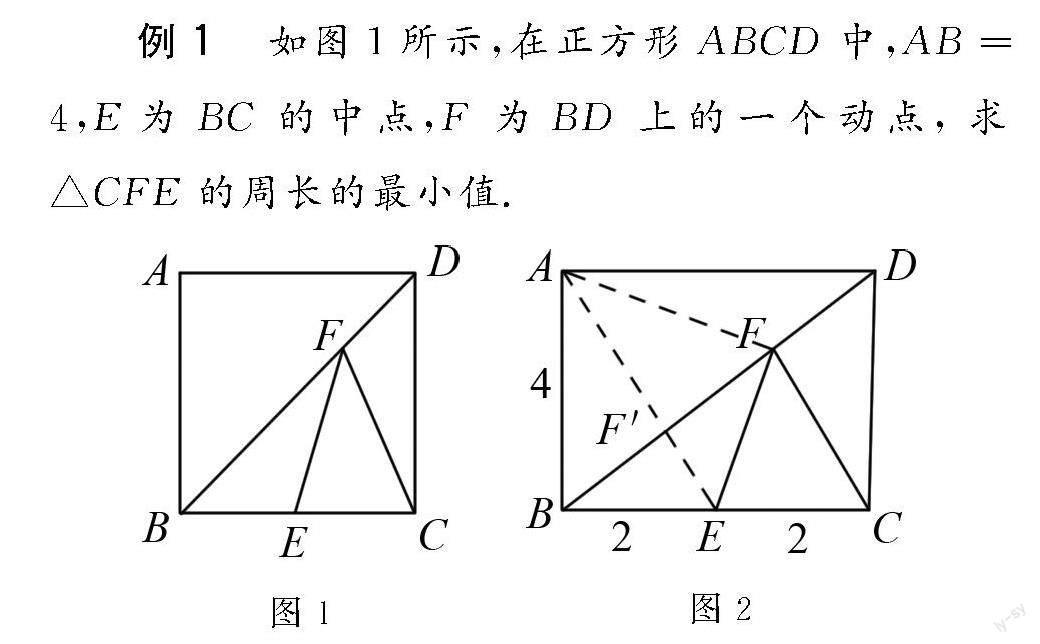
例1  如图1所示，在正方形ABCD中，AB=4，E为BC的中点，F为BD上的一个动点，求△CFE的周长的最小值.

解题思路  在正方形ABCD中，AB等于4，E为BC的中点，则BE和EC均为2，要求得△CFE的周长的最小值，则只需要求得EF+FC的最小值即可.而为了求得EF+FC的最小值，敏锐观察到这是初中数学典型的“将军饮马”“取中修路”模型的变形，特点是“两定一动”，BD就是“路”，E与C为“路”一侧的定点，F为动点.因此，顺势做AF连接线，如下图2所示，AF与FC沿着BD轴对称，其长度相同，EF+FC的最小值，即为EF+AF的最小值，很方便地观察到在F点（AE与BD的交点）时，得到EF+AF的最小值.解题思路清晰之后，再逐步去计算即可.

解题  由题意可知AB=4，BE=EC=2，△CFE的周长为EF+FC+EC

连接AF，AF与FC沿着BD轴对称，则EF+FC=EF+AF

∵F为BD上动点，EF+AF≥AE，

A、F、E三点共线的时候，EF+AF值最小

∴在F＇点（AE与BD的交点）时，得到EF+AF的最小值，

此时EF+AF=AE=

∴△CFE的周长的最小值为EC+AE=2+2√5

2.2  以形助数

面对一些较为复杂的数理关系，则利用画图的方式，用直观的图像将其呈现出来，去直观观察或分析图像的特点，进而对数理关系进行解答，得出答案.

例4  若a2+b2=5，求2a+3b的最大值？

解题思路  单纯进行计算并不容易，可通过数形结合的方式进行解答.第一步，观察到a2+b2=5，敏锐得知这是一个圆形，在横轴为a，纵轴为b的坐标系中以O为圆心做圆，则可得圆的半径为.第二步，观察2a+3b的最大值，则主要研究方向为将其转化为几何表达，设2a+3b=m，则可得b=-a+m，为b与a关联的一次函数，且该一次函数在圆的范围（与圆相交），那么就可以从图形中观察到，要求得m的最大值，就是一次函数b=-a+m与纵轴交点的纵坐标的最大值，而一次函数b=-a+m与圆a2+b2=5相切的时候，得到最大值，如图6所示.第三步，在图形上标记出数值，按照这一解题思路顺序，依次进行解答即可，解题过程则如下图7所示.

解答 如图6所示，圆形a2+b2=5，其半径为

设2a+3b=m，则可得b=-a+m

b=-a+m与圆a2+b2=5相交，在相切时可得m最大值

再如图7所示，b=-a+m与圆相切时，

与纵轴的交点为A（0，m），与横轴的交点为B（m，0）

在△AOB中，由勾股定理得AB=m

S△AOB=m·=m·m

∴m=

4 结语

综上所述，在初中数学解题中，数形结合是一个非常优秀的解题方法，将数与形这两个数学领域至关重要的因素结合起来，通过数与形之间的互通、转化，来解答数学习题，将繁复的数学习题用简单的方法解答出来.

参考文献：

[1]香钦源.数形结合思想在初中数学解题中的应用[J].数理天地（初中版），2023（17）：20-21.

[2]林越.数形相依 珠联璧合——数形结合思想在初中数学解题中的策略探究[J].数理化解题研究，2023（14）：17-19.

[3]杨远鸿.数形结合思想在初中数学解题中的应用——以初中函數问题为例[J].数理天地（初中版），2023（01）：52-53.

[4]王莹.试析数形结合思想在初中数学解题中的应用[J].科学咨询（教育科研），2022（07）：185-187.

[5]岳自利.数形结合思想在初中数学解题中的应用研究[J].数学大世界（下旬），2022（05）：71-73.