巧用一题多解提升高中生数学核心素养

郑米海

【摘要】在新课改推动下，高中数学教学越来越重视对学生数学核心素养的培养.在实际教学中，教师要立足课堂，聚焦素养，引导和鼓励学生多角度探究解决问题的方法，以此将培养学生数学核心素养落到实处.文章以一道典型的二元变量最值问题为例，从引导学生多角度、深层次挖掘题设信息，鼓励学生多视角思考问题，探寻多种解题方法等方面通过“一题多解”引导学生理解基础知识，掌握基本技能，积累基本活动经验、提炼基本思想方法，发展学生发现、提出、分析和解决问题的能力，促进学生数学核心素养的发展与提升.

【关键词】一题多解；数学核心素养；解题技巧

高中数学学习不仅要让学生掌握数学知识，而且要让学生获得进一步学习及未来发展所需的关键能力和必要品格.在新课改背景下，数学教育从关注“双基”走向“四基”，从关注提升“两能”走向“四能”，将培养学生关键能力和必要品格作为数学教学的重要课题.在实际教学中，教师应结合相应的教学内容设计有效的教学活动，引导学生多角度、多方位地探索知识，促进学生数学核心素养的形成和发展，促进“四基”与“四能”的培养与落实.

“一题多解”不仅可以锻炼学生的数学思维能力，而且可以拓宽学生的视野，优化学生的解题策略，其有利于发展学生数学核心素养，充分发挥数学教学的育人功能.因此在高中数学教学中，教师要充分发挥“一题多解”的作用，切实提升学生学习品质，确保课堂教学目标的达成.在高三复习教学中，教师应认真研读课程标准、全面了解学生学情，立足核心素养，结合教学实际精心挑选一些典型例题，引导学生从不同角度分析和解决问题，通过“一题多解”优化学生的认知结构，促进其数学核心素养的形成和发展，提高学生解题能力.以下笔者以一道二元变量最值问题为例，引导学生从不同视角去审视和探究问题，以此强化学生问题意识，凸显数学本质，让学生的数学核心素养得到提升.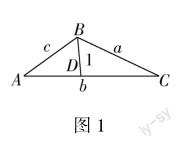

一、分析问题

例题 如图1所示，在△ABC中，∠A，∠B，∠C对应的边分别为a，b，c，∠ABC=120°，∠ABC的平分线交AC于点D，且BD=1，求4a+c的最小值.

该题是一道二元变量最值问题，看似简单，但是内涵丰富，解法多样，可以很好地考查学生的知识掌握情况，对备考有很好的导向作用.解题中，教师要引导学生多角度挖掘二元关系“ac=a+c”，通过方法联想，实现知识串联，促进“四基”的落实和“四能”的培养.解三角形问题是高考的重要考点，也是高中数学教学的重点内容之一.在研究解三角形的问题时，教师要打破就题论题的教学模式，关注数学知识间的内在联系，引导学生“会一题通一类”，有效提高学生数学知识应用能力.

设计意图 在本课教学中，教师引导学生从不同角度分析和解决问题，从而将对解三角形问题的研究拓展至对整个平面几何图形的研究，通过多视角探究将多个知识点、不同的数学思想方法有效地串联起来，逐步完善学生的认知结构，培养学生观察分析、数学抽象、逻辑推理、数学运算等综合能力和核心素养.同时，这一二元变量最值问题的解决，可以帮助学生巩固和强化解三角形和基本不等式的基本知识、基本方法，帮助学生积累基本活动经验，感悟转化与化归这一重要数学思想方法在解题中的重要作用.

二、解决问题

给出例题后，教师让学生以小组为单位共同探究.活动中，教师鼓励学生尝试从不同角度分析和解决问题，几分钟后，有的小组已经找到了思路，教师让学生呈现自己的解题思路，并以学生为主体展开讨论.

师：谁来说一说，你想如何求解呢？

师：很好，根据角平分线性质和向量相关知识，应用转化与化归思想成功地解决了问题.

教学思考 学习过程是一个发现和感悟的过程，教学中切勿急于将解题过程呈现给学生，应该提供机会让学生独立思考或合作探究，让学生的思维参与其中，以此确保问题的解决和能力的提升.教学中，教师要结合学生的知识储备和基本学情引入一些具有代表性的问题，并提供机会让学生研学讨论，让学生在互动交流中找到解决问题的突破口，积累基本活动经验，提升学生解题技能，有效培养学生的“四能”.

师：在解三角形边角有关的问题时，很容易联想到正弦定理、余弦定理，在解本题时，若从这个角度思考，你能想到什么呢？（学生积极思考）

教學思考 教师作为课堂教学的组织者和引导者，要充分发挥自身的引导作用，在学生迷茫的时候进行有效的启发和引导，以此拓宽学生的视野，帮助学生领悟问题的本质，提高学生解题技能.当然，若想发挥自身的引导作用，教师要充分地理解知识、理解学生，知晓解决问题的关键和核心，这样才能通过有效的引导帮助学生找到解决问题的突破口，发散学生的数学思维.在本课教学中，学生给出第一种解题方法后，教师没有急于结束本题的探究，而是引导学生结合解决三角形边角问题的经验进一步探索.这样在教师的指导下，学生借助余弦定理和正弦定理找准边与角之间的等量关系，顺利解决问题，有效地提升了学生发现、提出、分析和解决问题的能力.

师：以上主要是从“数”的角度分析，若从“形”的角度出发，你又能想到什么呢？（学生积极画图，结合图形寻找对应的等量关系）

生4的方案给出后，其他学生都自发地鼓掌.

师：非常好，利用面积法方便快捷地解决了问题.

教学思考 观察可能导致发现，因此教学中教师要有意识地引导学生从“形”的角度出发，借助“形”引导观察，揭示某种规律、模式、定理.在以上教学活动中，学生运用代数方法解决问题后，教师又启发学生从“形”的角度出发，通过几何图形充分挖掘已知条件，探寻其中蕴含的隐性联系，从而运用几何知识解决问题.学生通过观察发现三角形中的边角关系，运用熟练的面积法解决了问题.在此过程中，学生充分利用面积的可分性，将一个图形分解成两个三角形，借助等面积建立相应的关系式，形成清晰的解题思路，高效地解决了问题.其实正弦公式的推导有面积法，所以认真分析生3和生4的解题方法不难发现，两种方法虽然处理工具不同，但是其本质相同，具有异曲同工之妙.不过面积法更易于理解和掌握，合理应用有利于对学生直观想象、逻辑推理等素养的培养，也有利于增强学生解题信心，提升解题效率.

师：三角形是平面几何图形，若将这一几何问题代数化，可以以什么为载体来建构呢？

生齐声答：平面直角坐标系.

师：很好，该如何建系呢？（学生继续思考）

教学思考 引导学生运用代数法解决几何问题，可以让学生体会数形结合在解题中的优越性，培养学生的数形结合意识.在平时教学中，教师要有意识地引导学生应用代数方法研究几何问题，从而使问题变得更加具体，易于操作.对于本题，建系后，除了应用斜率相等建立等量关系外，也可以借助向量共线建立等量关系，还可以借助两点建立直线方程，然后另一点在直线上建立等量关系.教师可以启发学生尝试运用不同方法求解，以此夯实“四基”.

三、教学思考

（一）多角度审视问题，发展数学思维能力

众所周知，对于一个事物，若想认识其本质，必须从不同角度、不同方位来审视它，数学问题亦是如此.在本课教学中，教师启发和指导学生从不同角度思考和解決问题，帮助学生认清问题的本质.同时，通过“一题多解”可以极大程度地激发学生的潜能，帮助学生积累丰富的活动经验，促进学生思维能力的发展和解题能力的提升.另外，通过多角度探究，将多个知识点有效地建立联系，可以促进学生认知体系的优化，为数学应用打下坚实的基础.

在本课教学中，教师以典型问题为切入口，引导学生从平面几何视角、向量视角、正弦定理、余弦定理等多个视角审视问题，通过该题的解决让学生充分感知解题方法的多样性，有效培养学生的数学应用意识和创新意识，发展学生综合应用能力.

（二）以学生为主体，以教学为主导

课堂教学的主体是学生.教学中，教师应结合教学实际适度地“放权”给学生，鼓励学生独立思考和合作交流，让学生在思考与交流中形成自己的解题策略，以此有效提升学生解题技能，发展学生数学应用能力.在本课教学中，教师将解题的主动权交给学生，指导学生探寻不同的解题方法，以此增强学生的解题信心，让学生充分体会数学发现和数学探索的乐趣，引导学生主动学习.

当然，在强调学生主体价值的同时，教师的主导作用也不容忽视.如在本课教学中，多种解决方法的获得离不开教师的启发和指导.教学中，教师既要充分预设，又要及时捕捉生成，还要为学生提供时间和空间去自主探究，以此让学生更好地认识数学、理解数学，提高学生的数学核心素养.

结 语

总之，在高中数学教学中，教师应关注学生“四基”的落实和“四能”的培养，关注学生数学核心素养的培育.在解题教学中，教师要聚焦核心素养，认真研究题目，充分挖掘典型例题的教学功能，引导学生将新知与旧知有效地联系起来，通过“一题多解”发展学生的数学思维，提升学生综合应用能力，促进学生认知结构的优化和课堂效率的提升.另外，教学中，教师要为学生搭建一个独立思考和合作交流的舞台，提供机会让学生表达自己的所思、所想、所惑，以此通过多角度探究使得学生的知识结构得以优化，使得学生的思维能力得以发展，最终促进学生数学核心素养的发展与提升.

【参考文献】

[1]李修刚.核心素养视域下高中生数学“四能”的生成与发展[J].高考，2023（13）：64-66.

[2]周安勇.浅析高中数学一题多解教学模式对学生能力的促进探讨[J].数学学习与研究，2020（21）：143-144.

[3]李建清.高三数学教学落实核心素养的若干问题分析[J].高考，2019（33）：120.

[4]姜波.数学核心素养理念下高中数学教学的实践研究[J].求知导刊，2020（51）：35-36.