由度量诱导的集合列上(下)极限及其应用
李 杰, 孙明澎
(江苏师范大学 数学与统计学院,江苏 徐州 221116)
0 引 言
实变函数论是经典微积分学的继续与深化,同时也是点集拓扑、泛函分析、测度论等后继分析课程的必备基础.粗略地讲,实变函数论是基于Cantor集合论,从分割值域角度把函数的分析转化为集合的研究,从而在集合族上建立新的测度与积分的理论.和数学分析一样,极限仍是研究实变函数的重要工具.因此如何在集合族中合理定义极限,是实变函数论首要解决的基础问题.
众所周知,数列极限可用数列上(下)极限来刻画;当数列不收敛但有界时,上(下)极限总是存在,从而可用上(下)极限更好地描述数列极限点的分布.由数列上(下)极限可研究函数列的上(下)极限.对于不同对象的上(下)极限的定义,一般认为本质上都应起源于数列的上(下)极限的定义.因此,本文研究如何从数列上(下)极限的定义自然地引出q中集合列的上(下)极限定义.
通过查阅一批实变函数论教材,发现对集合列上(下)极限的定义引入较为突兀或难以理解其本质.例如,教材[1]直接抛出集合列上(下)极限的定义而未做出相关说明,导致很多学生不清楚集合列上(下)极限如此定义的原因及合理性.教材[2]采用类比思想,根据单调数列必有极限(若极限允许取值无穷),类比给出单调集合列的极限集定义.
定义1[2]对于q中集合列若对任意k,Ak⊂Ak+1,则称是递增集合列,这时称为的极限集,记为
(1)
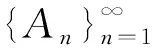
(2)
对于一般的集合列上(下)极限,可类比数列上(下)极限的做法得到.
定义2[2]对于q中任意集合列令关于k递减(关于k递增),定义的上、下极限集:
(3)
(4)

上(下)极限集有如下等价描述,教材[1,3]直接以此作为集合列上(下)极限的定义.

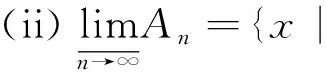
文献[4]通过类比的思想进一步阐述了数列上(下)极限与集合列上(下)极限思维方法的一致性所在.文献[5]给出了数列上(下)极限的一种分解策略,并运用其类比分析集合列上(下)极限.
综上所述,通过类比思想定义集合列上(下)极限相对而言更易理解.但这种方法只是在集合列上(下)极限与数列上(下)极限拥有相同形式的层面上,通过类比进行的分析和推导,并未解释集合列上(下)极限定义的思想根源,而且定义出来的集合列上(下)极限难以从欧式空间q推广到一般的空间.
下例说明集合列上(下)极限并不是数列上(下)极限的直接推广.
例1给定数列{an∈|n∈+},可构造单点集合列{An⊆|An={an},n∈+}.若令易验证:
鉴于实变函数论在分析学中的承上启下作用,本文将从数学分析数列上(下)极限出发,分析其本质,引入一种能推广到一般度量空间(甚至拓扑空间)的集合列上(下)极限定义,并研究其性质和应用.
1 本质分析
首先回顾(函)数列上(下)极限相关的定义,并强调度量结构在其中的作用.
定义3对于欧式度量空间(q,d)中数列{xn}n∈+和数a∈q∪{∞},若对任意ε>0,球形邻域Bd(a,ε)={x∈q|d(x,a)<ε}(∞处的邻域定义为Bd(∞,ε)={x∈q|d(x,0)>1/ε})中都含有数列{xn}n∈+中无限多个项,则称a为数列{xn}n∈+依度量d的聚点.

当度量d为绝对值度量|·|时,即为通常意义下的数列(上、下)极限,在不引起歧义的情况下相关记号省略上标d.
定义4[3]定义在E⊂q上的实值函数列{fn(x)}n∈+的上、下极限函数定义为
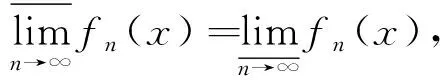
定义5设X⊂q为非空集合,A⊂X,则
称为集合A的特征函数.

注意到任意一列特征函数的上(下)极限仍为特征函数,于是可将该特征函数对应的集合定义为特征函数列对应的集合列上(下)极限,即
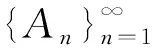
(5)
(6)

易验证定义6与定义2、命题1等价.
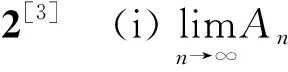
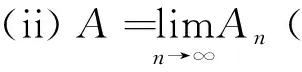
定义6的优点在于,通过数学分析函数列上(下)极限便可给出集合列上(下)极限.但是,这种定义方式对数学分析知识的掌握程度要求较高,大多数数学分析教材对于数列上(下)极限的内容尚且不够重视,有的甚至将其列入选学内容,对于函数列上(下)极限更是完全没有介绍.
受定义6启发,直接从数列上(下)极限定义出发,并强调度量d的作用,可给出如下定义:
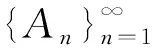
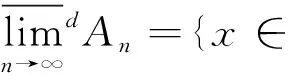
(7)
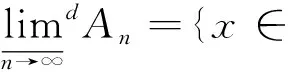
(8)
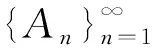
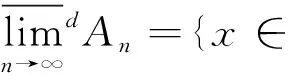
(9)
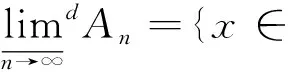
(10)
2 主要结果

定义9设A⊂q为一非空集合,定义ds:A×A→使得对于任意x,y∈A有
则称ds是A上的一个离散度量.
定理1q中集合列按定义2(或命题1、定义6)给出的上(下)极限等价于按定义8由离散度量ds诱导的上(下)极限,即
证注意到q上赋予离散度量ds时,对任意x∈q和任意0<ε<1有Bds(x,ε)={x},易见定义8中由离散度量ds诱导的上(下)极限集与定义2等价.
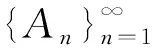
下面进一步研究由度量诱导的集合列上(下)极限的内在结构.
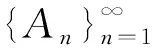
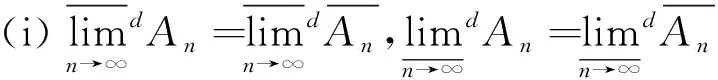
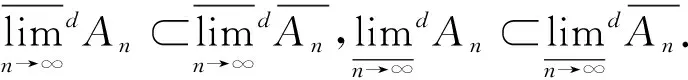
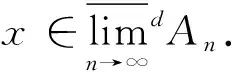

(ii) 由定义和(i)即得.
对任意ε>0和A⊂q,定义Aε={x∈q|∃y∈A,s.t.d(x,y)<ε}.



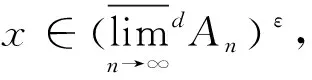
d(x,xn)≤d(x,y)+d(xn,y)<ε,
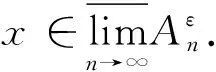
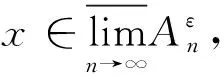
d(x,z)≤d(x,xnk)+d(xnk,z)<ε+1/k,
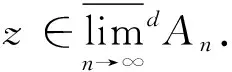
(iii) 先证必要性.对任意ε>0,由(ii)得
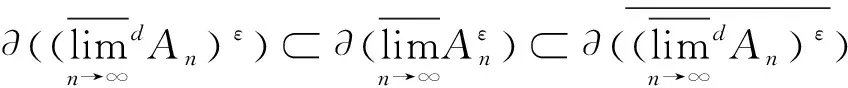
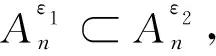
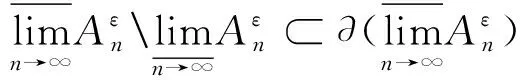
(iv) 由(iii)和(i)易得.
定理2(iv)的逆命题一般不成立.
易验证
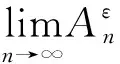
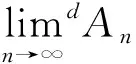

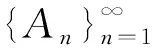
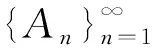

但对任意ε>0,有
易验证
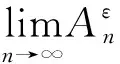
3 应 用
Lebesgue测度关于集合列极限具有一定的连续性.
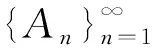
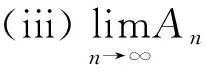
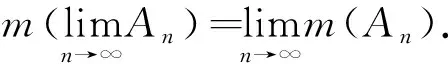
需要说明的是,定理3对一般的测度不一定成立[8].下面指出定理3可以推广到由度量诱导的极限情形.
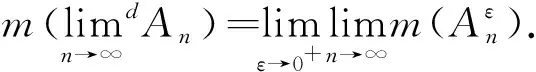
为证明定理4,需要下面的引理.
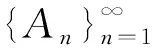
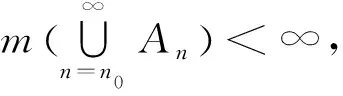
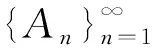
引理2设{At}t∈+是一族可测集合,且对任意t1 证任取单调递减数列tn∈+满足tn→0+(n→∞),则对任意ε>0,存在n满足ε>tn,则Aε⊃Atn,从而由此知A0是可测集. (11) (12) 根据定理2和引理2, (13) 对于不同对象的上(下)极限定义,本质上都应起源于数列的上(下)极限定义.在现行的大多数实变函数论教材中,仅通过类比思想对于集合列上(下)极限与数列上(下)极限的联系做出了形式上的解释,不利于学生对集合列上(下)极限定义本质的理解.本文基于特征函数列与集合列之间的关系,分析了集合列上(下)极限的思想根源.受此启发,从数列上(下)极限出发,介绍了一种由度量诱导的集合列上(下)极限概念,并研究其结构和性质.结果表明,通常的集合列上(下)极限本质上为由离散度量诱导的集合列上(下)极限,而且Lebesgue测度关于由度量诱导的集合列极限保持一定的连续性. 致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.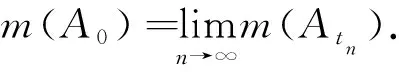
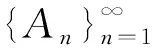
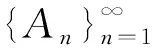

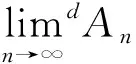
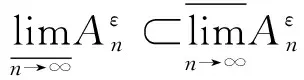
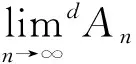
4 结 论

