最速下降法的一次迭代收敛性的一点注记
邱松强, 谢海燕
(1.中国矿业大学 数学学院,江苏 徐州 221116; 2.江苏师范大学 数学与统计学院,江苏 徐州 221116)
0 引 言
本文考虑如下的严格凸二次规划问题
(1)
其中G∈n×n是正定矩阵,b∈n,c∈.
最速下降法是求解无约束优化问题的最为常见算法之一[1-3].这种算法及其改进方法因为原理简单,较好的全局收敛性,计算量小,易于实现等特点而得到重视和应用, 如文献[4-7]等.特别值得一提的是近年来它们在机器学习领域的应用极为成功,如文献[8-9]等.
但是最速下降法的缺点和它的优点一样明显:收敛速度较慢. 在较为一般的条件下,它具有线性收敛速度,并且迭代过程中会产生著名的“锯齿 (Zigzag) 现象”[1-3]. 而相比之下,共轭梯度法、拟牛顿法等算法有更快的收敛速度[1-3,10],特别地,它们都具有二次终止性,即当算法被应用于严格凸二次规划 (1) 时,从任何初始点出发,最多经过n次迭代就可以得到问题的精确解[1-2]. 这样的对比使得学生容易把最速下降法当成一种十分“低效”的算法,并因此忽视其价值.
最速下降法并不具备二次终止性,但是当初始点x0满足一定条件时,算法将在一次迭代后得到 (1)的精确解[11].本文中,称一个算法在点x0处具有一次迭代终止性,如果以该点为初始点,算法将在一次迭代后得到 (1) 的精确解.按定义,二次终止性蕴含了一次迭代收敛性,反之不然.
本文进一步讨论了最速下降法的一次迭代收敛性,证明最速下降法在某初始点处具有一次迭代收敛性等价于它从该点出发可经有限次迭代后到达问题点最优解.这说明在求解 (1) 时,最速下降法或者一次迭代终止,或者无法在有限次迭代内达到精确解.本文的工作丰富了最速下降法的理论,有助于更好地认识和理解该算法.
1 特征值与特征向量
特征值和特征向量是线性代数中最具特色的内容之一.关于这部分的详细论述可参考线性代数教材或相关文献[12-14].这里只介绍其定义和几个在本文后续的讨论中将会被用到的性质.
定义1设A∈n×n,如果存在数λ∈和非零向量α∈n,使得Aα=λα,则称λ为A的特征值,称α为A的属于特征值λ的特征向量.
性质1矩阵A∈n×n的属于不同特征值的特征向量线性无关.
推论1设α1,α2∈n是方阵A的两个属于不同特征值的特征向量,则α1+α2必不是A的特征向量.
性质2设G∈n×n是对称矩阵,则G的每一个特征值都是实数.
性质3实对称矩阵G的属于不同特征值的特征向量是正交的.
性质4若G∈n×n是对称正定矩阵, 则G的特征值均大于零.
性质5设G∈n×n是对称矩阵,则G有n个线性无关的特征向量.
推论2设G∈n×n是对称矩阵,则对任意w∈n,存在G的属于不同特征值的特征向量v1,v2,…,vl,(l≤n),使得w=v1+v2+…+vl.
2 最速下降法及其基本性质
在任意x∈n处,若梯度∇f(x)≠0,则沿负梯度方向函数值下降最快,因此负梯度方向常被称为最速下降方向.1847年,Cauchy提出了一个基于最速下降方向的算法,即著名的最速下降法.
算法1最速下降法
步0 给定控制误差ε>0.取初始点x0.令k=0;
步1 计算∇fk=∇f(xk).若‖∇fk‖≤ε,则令x*=xk,算法终止;
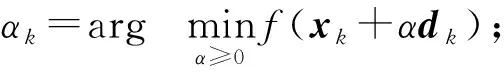
步3 令xk+1=xk+αkdk,k=k+1,转步1.
根据步2最优步长αk的计算公式可知
∇f(xk-αk∇f(xk))T∇f(xk)=0.
(2)
从而有
(3)
以下定理给出了最速下降法的收敛速度.
定理2[2]设{xk}是最速下降法应用于严格凸二次规划问题 (1) 时产生的点列,则有
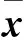
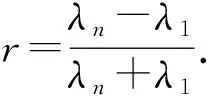
接下来的定理说明当初始点满足一定条件时,最速下降法只需一次迭代即可得到 (1) 的精确解.
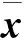
3 最速下降法在有限步内得到解的充要条件
定理3是一个比较常见的性质,经常出现在一些最优化教材的习题中.实际上,可以对该定理做一些扩展,考虑算法在有限次,而非仅一次迭代后得到问题的解.
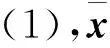
证由推论2,向量w可以表示成为G的几个属于不同特征值的特征向量之和,即存在分别属于特征值0<λ1<λ2<…<λl的特征向量v1,v2,…,vl, 使得w=v1+v2+…+vl.由于w不是G的特征向量故而l≥2.
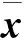
先考虑第一次迭代.设最优步长为α0,则由(3)知,α0≥1/λl>0.因
故


所以有
因此对任意1≤i≤l, 有
特别地,由λ1<λ2<…<λl知
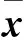
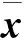
推论4设用最速下降法求解(1).从初始点x0出发,算法能经有限次迭代得到解的充要条件是算法经一次迭代得到解.
4 结 论
本文以矩阵特征值、特征向量及其基本性质为基础,讨论了最速下降法具备一次迭代收敛性,证明求解严格凸二次规划时,最速下降法的一次迭代收敛性等价于有限次迭代收敛性.本文的结果丰富了最速下降法的理论,对于认识、理解最速下降法有一定的理论价值,对最速下降法或梯度类算法的教学有一定的启发意义.同时,本文的结果对如何提高最速下降法的效率具有一定的启发性,这方面的工作正在进行之中.
致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.

