克罗内克积的特征向量

孙云欢 ，白红信

（1.保定学院 数据科学与软件工程学院，河北 保定 071000；2.北京工业大学 理学部，北京 100124）

矩阵的克罗内克积是一种特殊的矩阵乘积运算.矩阵的克罗内克积不受普通矩阵乘积对行数和列数的影响，它是任意大小的两个矩阵间的运算，虽然其运算较普通矩阵繁琐，并没有被充分、广泛地了解，但是在矩阵理论中具有广泛的应用，比如对于求解矩阵方程[1]具有很大的帮助，而且在其他领域中也有非常广泛的应用，比如电信技术[2]、信息处理、图像处理[3]等.

本文着重探究矩阵克罗内克积的特征向量，以克罗内克积基本运算性质为基础，利用矩阵理论的可对角化矩阵和相似矩阵作为桥梁，对一般矩阵的克罗内克积的特征向量进行探究，为人们更好地理解克罗内克积奠定基础.

1 预备知识

1.1 定义

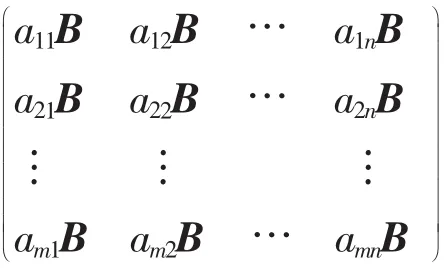
定义2[5]设矩阵A、B为数域P上的2个n阶矩阵，若存在可逆矩阵Q，使得Q-1AQ=B，则称矩阵A与矩阵B相似，记作A≈B.

1.2 引理

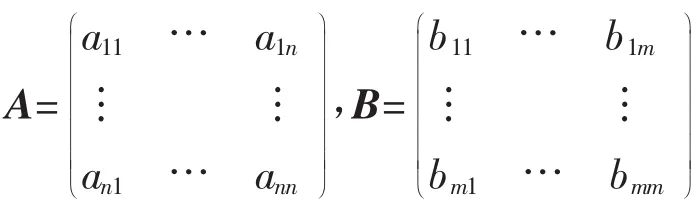
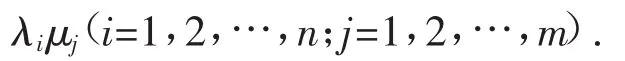
引理2[6]设存在可逆矩阵Q，满足Q-1AQ=B，μ是A与B的一个特征值.若β是矩阵B的属于特征值μ的一个特征向量，则Qβ是矩阵A的属于特征值μ的一个特征向量.

引理3[6]2个相似矩阵属于同一特征值的特征子空间同构.

2 矩阵的克罗内克积的特征向量

设矩阵A、B，已知矩阵A、B的特征向量，下面探究矩阵A、B的克罗内克积A⊗B的特征向量的表示形式.

2.1 可对角化矩阵的克罗内克积的特征向量

定理1 设矩阵A为n阶方阵，矩阵B为m阶方阵，且A、B为可对角化矩阵.设λ1、λ2、…、λn为矩阵A的特征值，μ1、μ2、…、μm为矩阵B的特征值，A的属于特征值λi的特征向量为αi（i=1，2，…，n），B的属于特征值μj的特征向量为βj（j=1，2，…，m），且α1、α2、…、αn线性无关，β1、β2、…、βm线性无关.则A⊗B的特征向量为

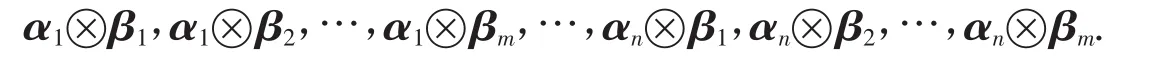
证明 由于 A、B 为可对角化矩阵，则存在可逆矩阵 T=（α1，α2，…，αn），P=（β1，β2，…，βm）使得

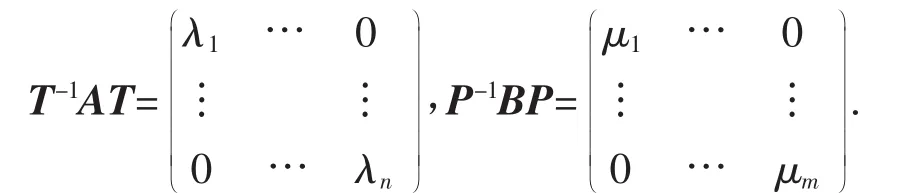
且有（T-1AT）⊗（P-1BP）=（T-1⊗P-1）（A⊗B）（T⊗P）=（T⊗P）-1（A⊗B）（T⊗P），且A⊗B也是可对角化矩阵，T⊗P为可逆矩阵，由A⊗B的特征向量构成.

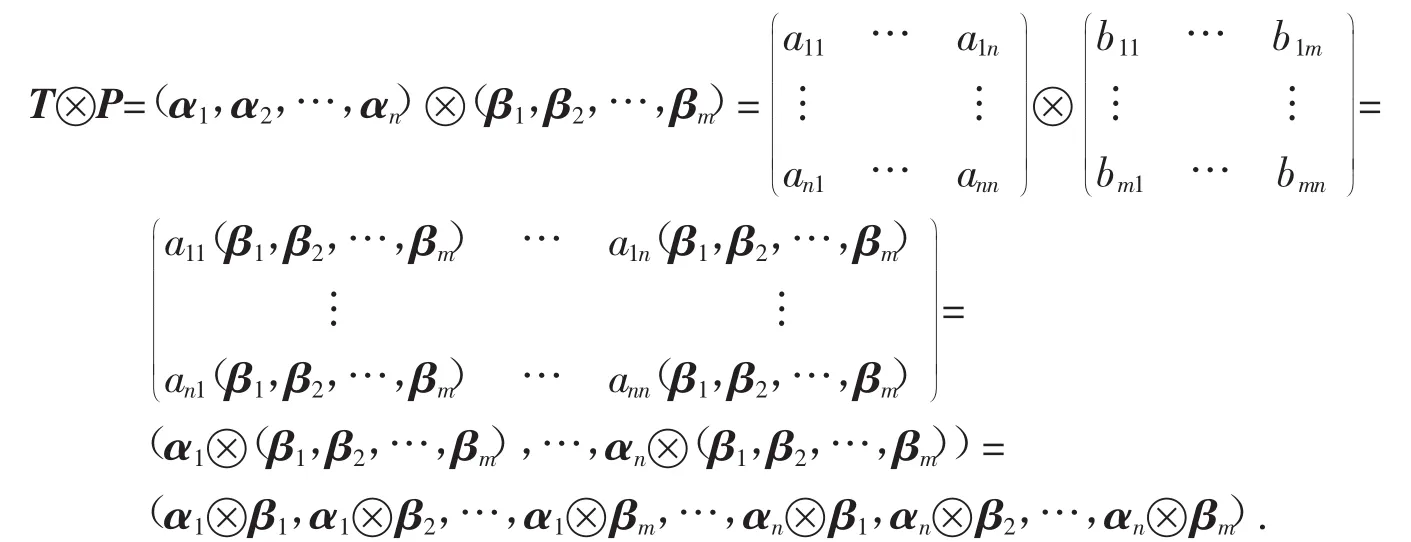
所以A⊗B的特征向量为

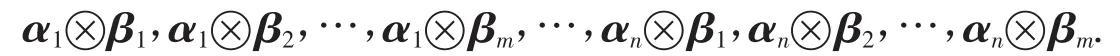
2.2 不可对角化矩阵的克罗内克积的特征向量

下面探究考虑当矩阵A、B为不可对角化矩阵且只有一个特征值的情形.

在线性空间的一组基下，线性空间中的每一个线性变换都与Pn×n中矩阵唯一对应.设线性变换V1在一组基 ε1、ε2、…、εn下的矩阵为 A，线性变换 V2在一组基 δ1、δ2、…、δn下的矩阵为 B，线性变换 V 在基 η1、η2、…、ηn2下的矩阵为A⊗B，又每个n级的复数矩阵A都与一个若尔当形矩阵相似.设n阶矩阵A、B为不可对角化矩阵且只有一个特征值.

2.2.1 命题

证明 可以计算得知矩阵M2的特征向量在基ε1、ε2下的坐标为e1=（0，1）T，N2的特征向量在基δ1、δ2下的坐标为 e1=（0，1）T.

令 P=M2⊗N2.

我们知道矩阵A⊗B的特征值为λμ，且相似矩阵有相同的特征值，则P=M2⊗N2的特征值也为λμ.设矩阵 P 的特征向量在基 η1、η2、η3、η4下的坐标为 X=（x1，x2，x3，x4）T.

1）若 λ=μ=0，则 x1=0，x2、x3、x4为任意常数.故矩阵 P 的特征向量在基 η1、η2、η3、η4下的坐标为（0，0，0，1）T，（0，1，0，0）T，即特征向量在基 η1，η2，η3，η4下的坐标为 e1⊗e1，e1⊗e2，e2⊗e1.

2）若 λ=0，μ≠0，则 x1=0，x2=0，x3、x4为任意常数.故矩阵 P 的特征向量在基 η1、η2、η3、η4下的坐标为（0，0，0，1）T、（0，0，1，0）T，即特征向量在基 η1、η2、η3、η4下的坐标为 e1⊗e1，e1⊗e2.

3）若 λ≠0，μ=0，则 x1=0，x3=0，x2、x4为任意常数.故矩阵 P 的特征向量在基 η1、η2、η3、η4下的坐标为（0，0，0，1）T、（0，1，0，0）T，即特征向量在基 η1、η2、η3、η4下的坐标为 e1⊗e1，e2⊗e1.

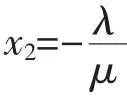
证明 令P=M3⊗N3.

我们知道矩阵 M3、N3的特征向量分别在基 ε1、ε2、ε3和基 δ1、δ2、δ3下的坐标都是 e1，矩阵 P 的特征值为 λμ，设特征向量在基 η1、η2、…、η9下的坐标为 X=（x1，x2，…，x9）T.

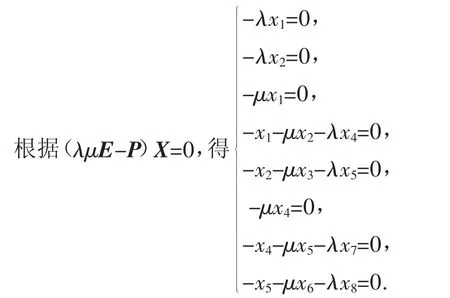
1）若 λ=μ=0，矩阵 P 的特征向量在基 η1、η2、…、η9下的坐标为

e1⊗e1，e1⊗e2，e1⊗e3，e2⊗e1，e3⊗e1；

2）若 λ=0，μ≠0，矩阵 P 的特征向量在基 η1、η2、…、η9下的坐标为

e1⊗e1，e1⊗e2，e1⊗e3；

3）若 λ≠0，μ=0，矩阵 P 的特征向量在基 η1、η2、…、η9下的坐标为

e1⊗e1，e2⊗e1，e3⊗e1；

4）若 λ≠0，μ≠0，矩阵 P 的特征向量在基 η1、η2、…、η9下的坐标为

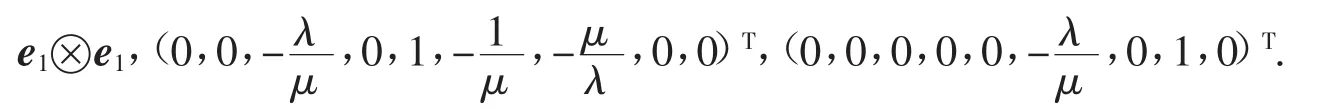
2.2.2 例题

例题1 考虑n阶矩阵A、B，设

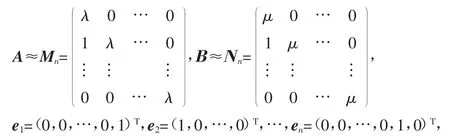
求解矩阵A⊗B的特征向量.

解 令矩阵P=Mn⊗Nn.

矩阵 Mn、Nn分别在基 ε1、ε2、…、εn和基 δ1、δ2、…、δn下的坐标都为 e1，矩阵 P 的特征值为 λμ，设 P在基 η1、η2、…、ηn2下的坐标为 X=（x1，x2，…，xn2）T，则由归纳法得：

1）当 λ=μ=0 时，矩阵 P 的特征向量在基 η1、η2、…、ηn2下的坐标为 e1⊗e1，e1⊗e2，…，e1⊗en，en⊗e1，en-1⊗e1，…，e2⊗e1，共有 2n-1 个特征向量.

2）当 λ=0，μ≠0 时，矩阵 P 的特征向量在基 η1、η2、…、ηn2下的坐标为 e1⊗e1，e1⊗e2，…，e1⊗en，共有n个特征向量.

3）当 λ≠0，μ=0 时，矩阵 P 的特征向量在基 η1、η2、…、ηn2下的坐标为 e1⊗e1，e2⊗e1，…，en⊗e1，共有n个特征向量.

4）当 λ≠0，μ≠0 时，矩阵 P 的特征向量在基 η1、η2、…、ηn2下的坐标为

所以矩阵P的特征向量共有n个，可以给上述自由未知量赋n组值，令分别为（1，0，0，…，0），（0，1，0，…，0），（0，0，1，…，0），…，（0，0，0，…，1，0），（0，0，0，…，1）.

于是便得到矩阵P的特征向量，其中一个特征向量在基下的坐标为e1⊗e1.

我们得知了2个若尔当形矩阵的克罗内克积的特征向量，因为矩阵A、B分别和若尔当形矩阵相似，即A≈Mn，B≈Nn.故存在数域P上的可逆矩阵Q1和Q2，使得数域P上的矩阵A、B满足

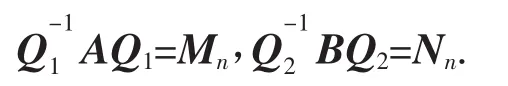
我们已经知道了矩阵Mn⊗Nn的特征向量，并记特征向量为β，且

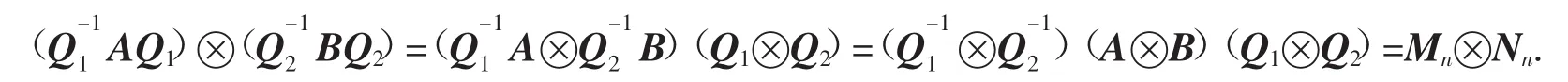
由引理2，则（Q1⊗Q2）β是A⊗B属于特征值λμ的一个特征向量.

这样我们就求得了矩阵A⊗B的特征向量.

3 结论

1）当2个矩阵都为可对角化矩阵时，这两个矩阵的克罗内克积的特征向量就是它们的特征向量分别作克罗内克积.

2）当2个矩阵为不可对角化矩阵时，它们的特征向量分别作克罗内克积一定是它们的克罗内克积的特征向量.若这2个矩阵都为n阶矩阵，可分为3种情况：如果这2个矩阵的特征值都为0，则它们的克罗内克积的特征向量共有2n-1个；如果这2个矩阵的特征值其中一个为0，另一个不为0，则它们的克罗内克积的特征向量共有n个；如果这2个矩阵的特征值都不为0，则它们的克罗内克积的特征向量共有n个.

本文只研究了2个可对角化矩阵的克罗内克积的特征向量和2个不可对角化且只有一个特征值的矩阵的克罗内克积的特征向量，对于不可对角化有多个特征值的矩阵的克罗内克积的特征向量还有待进一步研究.