不定积分中的课程思政元素赏析
严亚强, 顾振华
(苏州大学 数学科学学院,江苏 苏州 215006)
0 引 言
不定积分是微积分课程中的一个基础性章节,主要探讨计算原函数的基本技能,理论上的讨论很少,被认为较为平淡乏味的部分.但如果在不定积分的章节中放入一些课程思政的“盐”,是可以让学生体味这一部分的深刻的思想性的,并达到提升数学素养的目的.从中国知网的论文库中发现了一些课程思政元素,也发现了不少不定积分或课程思政相关的教学研究成果[1-3],结合多年教学和教材编写的实践,整理出用课程思政的观念进行不定积分教学的体会和建议,供参考.
1 精益求精的工匠精神
工匠精神,狭义地说是精益求精的工作作风;广义地说,就是追求真理、追求至善、追求完美的道德品质和人文精神.
1.1 工匠的求真精神

但仔细观察后可以发现,原函数的定义范围变成x≠0了,因此还需将最后一步推进到
同理
但这个函数在x=0处变的不连续了,这时可以化为
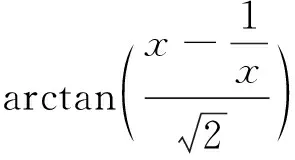

1.2 工匠的至善精神


结果都是对的,但哪种结果在形式上最可取呢?由公式tan2x+1=sec2x可见,tanx比其他函数更“亲近”于secx,容易相互替换,因此第三种形式最为可取.
在解决任何数学问题时,要像机械修理师那样,有意识地区分材料和工具.例如,在极限、求导和积分的计算中,常用极限、求导公式和基本积分公式是钉子、是材料,极限、求导的法则和积分性质是锤子、是工具;数学中大量复杂艰深的问题就像一台台机器,透过材料和工具的不断组装,形成很多板块上的组件,作为高级别的材料.例如,不定积分

就是学习工匠需要熟悉的材料,记住了就容易得心应手地做更复杂的不定积分.
1.3 工匠对完美的追求
所谓“美”,就是完美,就是对对称、简洁、完整等特性的追求.例如求解不定积分
传统地在分母上展开是十分烦琐的,一般都会寻求简洁的计算方法,如果写成
就十分有美感了.
数学之美还体现在方法之美和创新的奇异之美,这可以从后面的很多实例中看到.
2 坚忍不拔的创新精神
学习数学总是要与困难打交道的,坚忍不拔的精神是必要的科学态度.但科学事业的核心是创新精神,没有创新就不会有数学上的任何成就.
2.1 追求真善美是创新的动力
追求真善美是人类进步的共同价值观.这里所说的创新精神是科学素养,是比工匠精神更高的一种境界.
2.1.1 基于批判性思维的求真
例如,在学完不定积分的第二类换元法时,和学生研讨不定积分的换元定理时,即
定理1[4]设x=Ψ(t)是单调的可导函数,并且Ψ′(t)≠0.又设f[Ψ(t)]Ψ′(t)具有原函数,则有换元公式
其中Ψ-1(x)是x=Ψ(t)的反函数.
就要问:这个定理中,Ψ′(t)≠0的条件是必要的吗?应用的时候需要检验吗?
学生通过一阶段的解题实践,自然都会表示,Ψ′(t)≠0这个条件从来没有检验过,考察定理的证明:设f[Ψ(t)]Ψ′(t)的原函数为Φ(t),则
应该思考:如果定理换一个证明方法,能否把Ψ′(t)≠0这个条件省去呢?

2.1.2 基于发散性思维的求善和求美
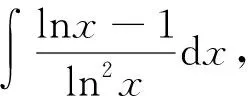
问题在于,能否取一个函数h(x),使得h′(x)f(x)-h(x)f′(x)=g(x),而这是一个一阶线性微分方程的问题.

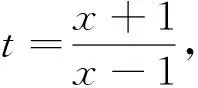
由此发现高次根式积分的一些规律,这就是数学之善与美!马克思说:劳动创造了美,的确精辟!
2.2 不定积分中是创造性思维的能源库
由于不定积分是求导运算的逆运算,这种运算的性质很少,只有线性性质可用,所以在计算时需要调动一切积极力量,包括直觉思维(一种结果先于演绎的思维)、猜想、试验等.
创造性是数学的本质,庞加莱用组合和选择描述创造的过程,克鲁捷茨基用思维灵活性理解数学创造力本质,也有数学家用发散性思维结果来刻画数学创造力,甚至用杰出数学家的思维特征来定义数学创造力.
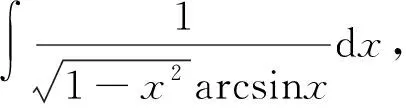

霍兰兹(Hollands)提出数学创造性表现的五个方面(灵活性、精致化、流畅性、独创性、敏感性),上面的这个例子已经体现得淋漓尽致!因此,不定积分的习题和问题充满着创造性思维的亮点,不定积分这一章就是创造性思维的一个能量库!马克思主义的实践观的实质就是创新精神,我们应该在科学知识的学习中培养研究和探索的习惯,提升发散性思维的本领,为人类进步多作贡献.
3 和谐共存的合作精神
和谐共存的合作精神是道德品质和人文精神的重要标志,也是立德树人的终极目标.在不定积分的教学中,可以感悟到很多这方面的存在.
3.1 多题协同探究实现数学抽象
日本数学教育家米山国藏在《数学的精神、思想和方法》一书中概括了七种数学精神,其中第一条是应用化精神(包括对数学本身的应用),第二条是“充满在整个数学中的扩张化、一般化精神”[6],这一条实际上就是指“数学抽象”,这也是我国2017年发布的六大数学核心素养之核心.在不定积分中,将多个题目联合在一起,探究共性,可以获得很多规律.例如,探究不定积分

通常,不定积分都会有“有理函数的积分”这一节,它强调的是一个一般性结论“任何有理函数都是‘积得出’的”,而这个结论是基于对积分
的“积得出”的肯定.
3.2 团结互助的生态文明
在不定积分中,你可以看到一个活生生的“和谐社会”.
3.2.1 积分可以结伴互助
2I1+3J1=x+C, 2I1-3J1=ln|2sinx+3cosx|+C.


3.2.2 积分可以互相启发,互相分担
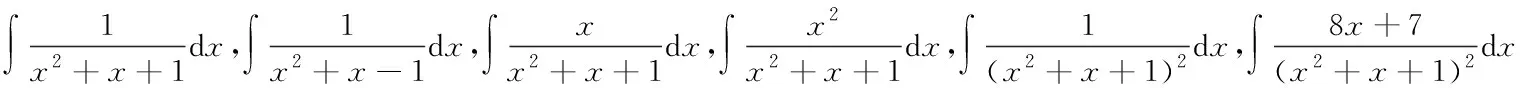
又如,用不定积分的裂项法可知,
这多像妈妈把一件家务事分配给几个孩子去做一样!
3.2.3 积分可以相互帮扶,“敬老爱幼”
例如,不定积分的分部积分公式

中的两个积分多么像两个团结友爱的同学,一个人解决不了问题时,另一个帮助解决!

否则很难解出.
3.2.4 积分可以协力化解危机
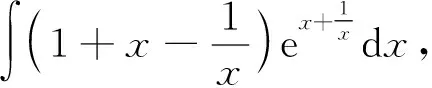
后面那个积分对前面的说“兄弟别急,站在那儿别动,我用分部积分法让咱俩一起逃离险情!”果然:
4 结 论
数学教育中的德育价值主要体现在道德品质、科学素养、人文精神三个方面.而工匠精神、创新精神、合作精神分别是这三个方面的核心,不定积分的数学文化背景不很丰富,但依然不失为课程思政的良好载体.我们在高等数学教学中,应充分挖掘数学中体现的文化和精神,引导学生感悟真善美的无处不在.
致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.

