双侧参数假设检验中原假设的选择

金百锁

(中国科学技术大学 统计与金融系,合肥 230026)

0 引 言

概率论与数理统计是大学所有理科专业的公共必修课,很多文科专业也需要开设统计学这门课程.在统计学教学当中,最重要的是统计思维的训练.美国科学院院士C.R.Rao教授认为“在理性的基础上,所有的判断都是统计学”[1],因此假设检验在统计思维训练中占有十分重要的地位,包含了很多统计思想,也是当今讨论最多的部分,例如2018年,72位作者一起在Nature子刊发表了一篇论文建议降低在众多实验中使用的显著性水平[2],引来了87 位作者一起发表的反驳论文[3].

关于假设检验的一些统计思想在陈希孺院士的教材中有详细的介绍[4].本文讨论的假设检验理论是1828年发展起来的奈曼-皮尔逊假设检验,这一理论需要控制第一类错误,导致假设检验中的原假设和对立假设有不同的地位.因此一般的原假设设立原则,是把不希望被轻易否定的假设,或者已经经历了一段时间考验的假设,设为原假设[4].而这一原则在教材中通常只针对于单侧检验[5-7].对于双侧参数假设检验,只把参数相等的假设设为原假设,而参数不等的假设设为对立假设.为什么不能把参数不相等的假设设为原假设,是因为在这个原假设下第一类错误不好计算吗?这一问题在教材中解释的并不详尽,本文的目的是分析一下这个问题,并给出一些统计解释.

1 双侧假设检验问题

大学的统计学教材,都是从正态分布总体的参数检验开始介绍.因此本文以正态分布总体的双侧参数假设检验为例.假设X1,…,Xn为独立同分布服从正态分布N(μ,σ2),σ2已知,检验μ=μ0这一假设,并放在对立假设,即检验问题是

H0∶μ≠μ0↔H1∶μ=μ0.

(1)

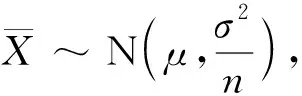
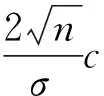
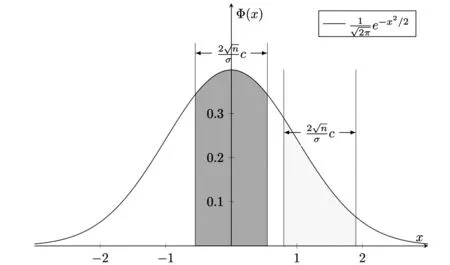
图1 标准正态区间概率示意图

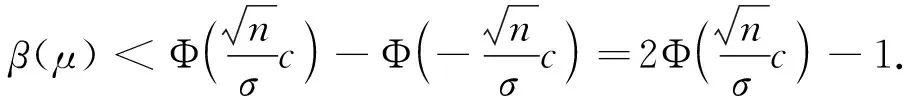
然而在这个拒绝域的条件下,第二类错误为

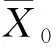
2 实 例

假设某一工厂声称其生产的一个合格的精密元件的长度服从正态分布,其均值为900mm,方差为100mm,现从一批元件中随机抽取25件,测得其平均长度为901mm,试在显著水平α=0.05下,确定这批产品是否合格.

解 法1建立假设

H0∶μ=900 ↔H1∶μ≠900.

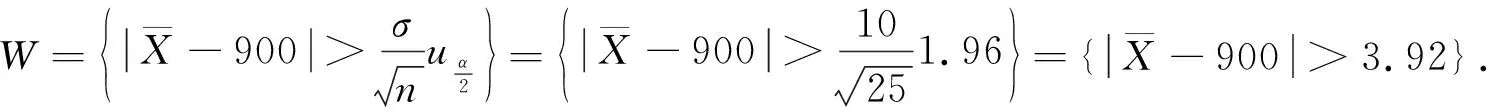
法2建立假设

H0∶μ≠900 ↔H1∶μ=900.

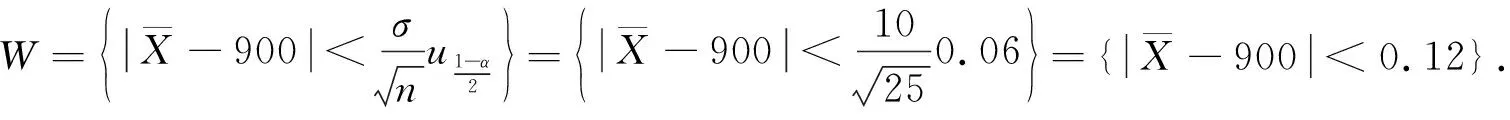
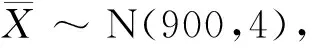
3 结 论

基于上面的分析,在保证第一类错误小于α的条件下,对于正态总体,如果原假设是μ≠μ0,则在一次试验中,都几乎不可能接受μ=μ0这一对立假设,即使这一对立假设是真实成立的.其背后的原因,应该是μ=μ0这一点相对于μ的全部参数空间的取值可以忽略不记,对立假设只有一个取值μ=μ0和原假设的参数空间几乎不可分.

上节构造的检验不是好的检验,因为功效函数β(μ)在对立假设μ=μ0下达到最大值α,这个功效太小了.一个好的检验,都需要在检验参数远离原假设参数空间的时候,或参数离原假设参数空间有一定距离但样本量趋于无穷时,功效函数趋于1,而当μ=μ0作为对立假设时无法做到远离原假设或有一定距离.

显著性假设检验的目的是,通过样本验证是否有足够的证据拒绝原假设.当μ≠μ0为原假设的时候,即使这个原假设不成立,通过上面的分析发现在正态分布总体下无法找到合适的检验有足够的证据能拒绝这个原假设.因此本文的结论是μ≠μ0不能作为原假设.

推荐的解决方案是:不再强求μ=μ0,构建一个新的检验,即用下式

H0∶|μ-μ0|≥Δ↔H1∶|μ-μ0|<Δ,

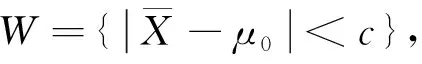
致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见,以及加拿大约克大学吴月华教授和中国科学技术大学王学钦教授提出的宝贵意见.