转化题目条件 探寻运动路径

苏国东

［摘  要］ “说题”是提升教师教学水平，促进教师专业化发展的有效途径. 文章从审题分析、解题过程、总结提升三部分“说”一道菱形综合题.

［关键词］ 说题；转化条件；运动路径；菱形综合题

“说题”是教师钻研教材、探讨教法、提升教学水平的有效手段，也是促进教师专业化发展的重要途径. 数学说题流程一般由三部分构成，一是审题分析，包括题目涉及的知识点、重难点和关键点，分析学情，挖掘隐含条件；二是解题过程，包括解题思路和方法；三是总结提升，反思解题过程，对题目进行必要的变式拓展.

本文从审题分析、解题过程、总结提升三部分“说”一道菱形综合题，以期抛砖引玉.

题目  如图1所示，在菱形ABCD中，∠DAB=60°，AB=2，点E是边AB上的一个动点，延长BA到点F，使AF=AE，且CF，DE相交于点G.

（1）当点E运动到AB中点的位置时，证明：四边形DFEC是平行四边形.

（2）当CG=2时，求AE的长.

（3）当点E从点A的位置向右运动到点B的位置时，求点G运动路径的长度.

审题分析

1. 题目概述

本题是在含60°角的菱形上添加三条线段设计而成的几何综合题. 本题立足基础知识和基本技能，发展学生的思维能力. 本题涉及的知识点包括平行四边形的判定定理、菱形的性质、相似三角形的判定定理和性质、等腰三角形的性质、勾股定理、锐角三角函数、点的运动轨迹等，考查学生的推理能力、画图能力、转化思想、方程思想等. 学生对菱形等基本图形性质的掌握较为扎实，具备一定的几何推理能力，但对动点轨迹问题较为陌生，求解本题存在一定的困难.

2. 条件分析

本题的主干条件有：含60°角的菱形ABCD，边长为2，AF=AE. 隐含条件是：平行相似，含60°角的特殊三角形.

第（1）问增加的条件是点E在AB的中点处，隐含条件是FE=AB=CD，对边存在平行和相等的关系.

第（2）问增加的条件是CG=2，隐含条件是DC=CG，△CDG是等腰三角形.

第（3）问增加的条件是点E从点A的位置运动到点B的位置，隐含条件是点E的运动路径、起点和终点，且点G随着点E的运动而运动.

3. 重难点和关键点

本题的第（1）问属于基础题，解决关键是选择合适的平行四边形的判定方法. 第（2）问先要构造相似或直角三角形，再利用方程思想、勾股定理、锐角三角函数求解. 第（3）问是动点轨迹问题，也是本题的难点，解决关键在于动手画图、合理猜想，探寻点G的运动轨迹. 初中常见的运动轨迹主要是直线形和圆弧形.

解题过程

寻找思考切入口，逐个分解、转化题目条件，找到解题路径和方法，完善解题过程.

1. 第（1）问的解答过程

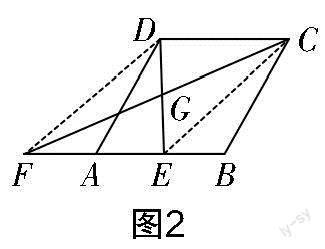
思考切入口：如图2所示，连接DF，CE，发现四边形ABCD和四边形DFEC存在公共边DC，利用判定方法“一组对边平行且相等”来证明四边形DFEC是平行四边形.

由条件1“菱形ABCD”得知DC=AB，DC∥AB.

由条件2“AF=AE”得知FE=2AE.

由条件3“E在AB的中点处”得知AB=2AE，所以AB=FE.

所以DC=FE，DC∥FE，因此四边形DFEC是平行四边形.

2. 第（2）问的解答过程

思考切入口：由题目所给条件可知△CDG是等腰三角形，借助平行相似转化数据，建立方程后求出线段的长.

由条件1“菱形ABCD”得知CD=CB=AB=AD=2，DC∥AB，故△DGC∽△EGF.

由条件2“CG=2，CD=2”得知△CDG是等腰三角形，根據平行相似得到△FGE也是等腰三角形.

设AE=n，由条件3“AF=AE”可得FG=FE=2n.

由条件4“∠DAB=60°”得知∠FBC=120°，于是从图中提取一个含120°的特殊三角形FBC（如图3所示），其中FC=2n+2，FB=n+2，BC=2.

3. 第（3）问的解答过程

思考1：点G的运动路径是什么？

（1）画图.

画出两动点的不同位置. 当点E分别在点A，E1，E2，B处时，连接DE和CF，得到点G依次位于点A，G1，G2，G3处，如图4所示，观察到点G的运动轨迹是从点A到G3的一条线段.

（2）猜想.

点G随着点E的运动而运动，可看作伴随轨迹问题，其中点E是主动点，点G是从动点，点E的运动路径是一条线段，则点G的运动路径也是一条线段. 通过几何画板动态演示也可以得到同样的结果.

（3）类比.

第（1）问与第（3）问的图形之间存在一定的关系. 第（1）问中的四边形DFEC是平行四边形，如图5所示，延长AG交DC于点H，点A，G分别是FE，DE的中点，所以AG∥FD，点H是DC的中点. 随着点E的运动，平行四边形DFEC变成了梯形，但不难推断点H仍是DC的中点. 说明AH与定线段DC交于定点H，所以点G的运动路径在直线AH上.

思考2：如何用初中知识来证明点G的运动路径是一条线段？

思考切入口：根据上述思路，如图6所示，延长AG交DC于点H，利用菱形中与AH有关的“8字形相似”模型，转化线段比例关系.

结合条件2“AF=AE”得知DH=HC，所以点H是DC的中点，为定点，所以点G在直线AH上运动.

由条件3“点E从点A的位置向右运动到点B的位置”得知点E的起点为A，终点为B，所以点G的起点为A，终点为K，如图7所示，即点G的运动路径为线段AK.

思考3：如何求线段AK的长？

思考切入口：利用三角形相似的性质、勾股定理、锐角三角函数等求线段AK的长.

在菱形ABCD中，∠DAB=60°，点H为DC的中点，连接BH构造直角三角形HBC.

此外，通过构造其他辅助线也可求得AK的长（如图9、图10所示）.

思考4：能否建立平面直角坐标系，用代数法解决几何问题？

思考切入口：求两直线的交点，即联立直线方程求公共解；求线段的长，可使用两点间的距离公式.

总结提升

1. 反思解题过程

本题三个小问的难度呈梯度变化，体现“使不同层次的学生得到不同发展”的理念. 第（1）问从已知四边形和待证四边形存在公共边的角度入手，通过“一组对边平行且相等”判定平行四边形. 第（2）问挖出隐含条件，借助平行相似、等腰三角形等知识，提取基本图形，构造含120°角的特殊三角形，运用勾股定理、锐角三角函数求解. 第（3）问通过动手画图、猜想验证和严谨推理，明晰动点的运动轨迹，逐步分解转化难点，利用几何和建系的方法求解，渗透着数形结合思想方法，是初高中知识衔接的良好体现.

2. 变式

第（3）问可变式如下.

（1）改变问题（条件相同）.

变式1：求点G的运动路径长度的取值范围.

变式2：求点G到AB的最大距离.

变式3：求△ABG面积的最大值.

（2）改变背景.

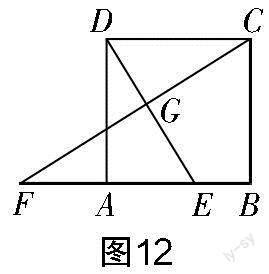
变式4：如图12所示，在正方形ABCD中，AB=2，点E是边AB上的一个动点，延长BA到点F，使AF=AE，且CF，DE相交于点G. 当点E从点A向右运动到点B的位置时，求点G运动路径的长度.

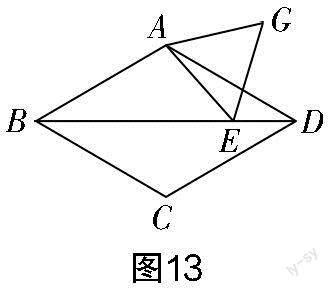
变式5：如图13所示，在菱形ABCD中，∠ABC=60°，点E是对角线BD上的一个动点，以AE为边作等边三角形AEG. 当点E从点B的位置向右运动到点D的位置时，求点G运动路径的长度.

变式6：如图14所示，在正方形ABCD中，AB=2，点E是边AB上的一个动点，△DEF为等腰直角三角形，点G是斜边DF的中点. 当点E从点A的位置向右运动到点B的位置时，求点G运动路径的长度.