说题有道 讲题有法

高慧

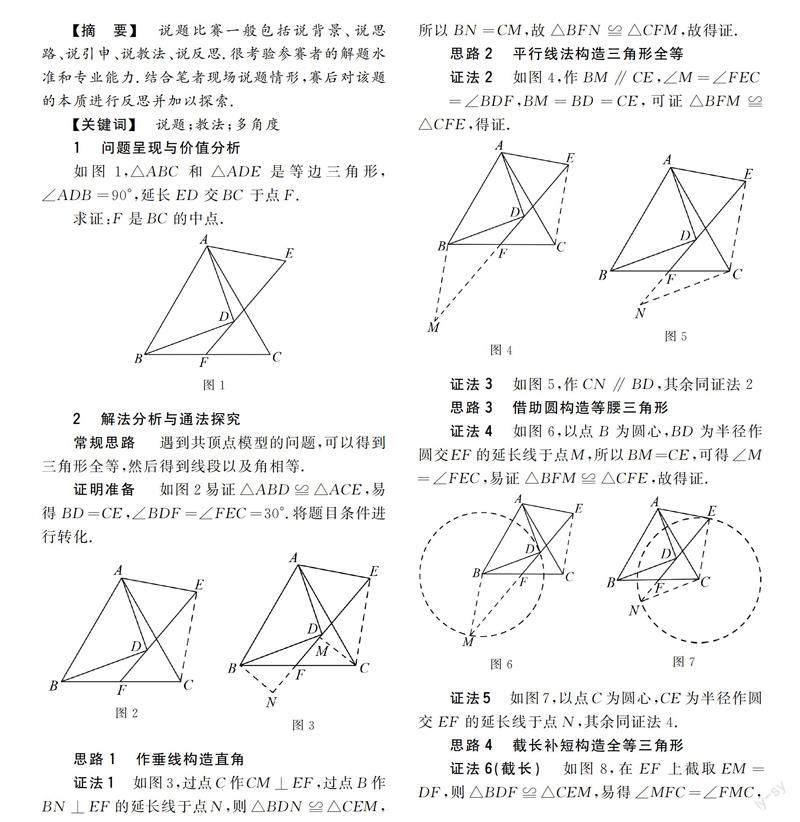
【摘要】说题比赛一般包括说背景、说思路、说引申、说教法、说反思.很考验参赛者的解题水准和专业能力.结合笔者现场说题情形，赛后对该题的本质进行反思并加以探索.

【关键词】说题；教法；多角度

1 问题呈现与价值分析

如图1，△ABC和△ADE是等边三角形，∠ADB=90°，延长ED交BC 于点F.

求证：F是BC的中点.

2 解法分析与通法探究

常规思路 遇到共顶点模型的问题，可以得到三角形全等，然后得到线段以及角相等.

证明准备 如图2易证△ABD≌△ACE，易得BD=CE，∠BDF=∠FEC=30°.将题目条件进行转化.

思路1 作垂线构造直角

证法1 如图3，过点C作CM⊥EF，过点B作BN⊥EF的延长线于点N，则△BDN ≌△CEM，所以BN=CM，故△BFN ≌△CFM，故得证.

思路2 平行线法构造三角形全等

证法2 如图4，作BM∥CE，∠M=∠FEC

=∠BDF，BM=BD=CE，可证△BFM≌△CFE，得证.

证法3 如图5，作CN∥BD，其余同证法2

思路3 借助圆构造等腰三角形

證法4 如图6，以点B为圆心，BD为半径作圆交EF的延长线于点M，所以BM=CE，可得∠M=∠FEC，易证△BFM≌△CFE，故得证.

证法5 如图7，以点C为圆心，CE为半径作圆交EF的延长线于点N，其余同证法4.

思路4 截长补短构造全等三角形

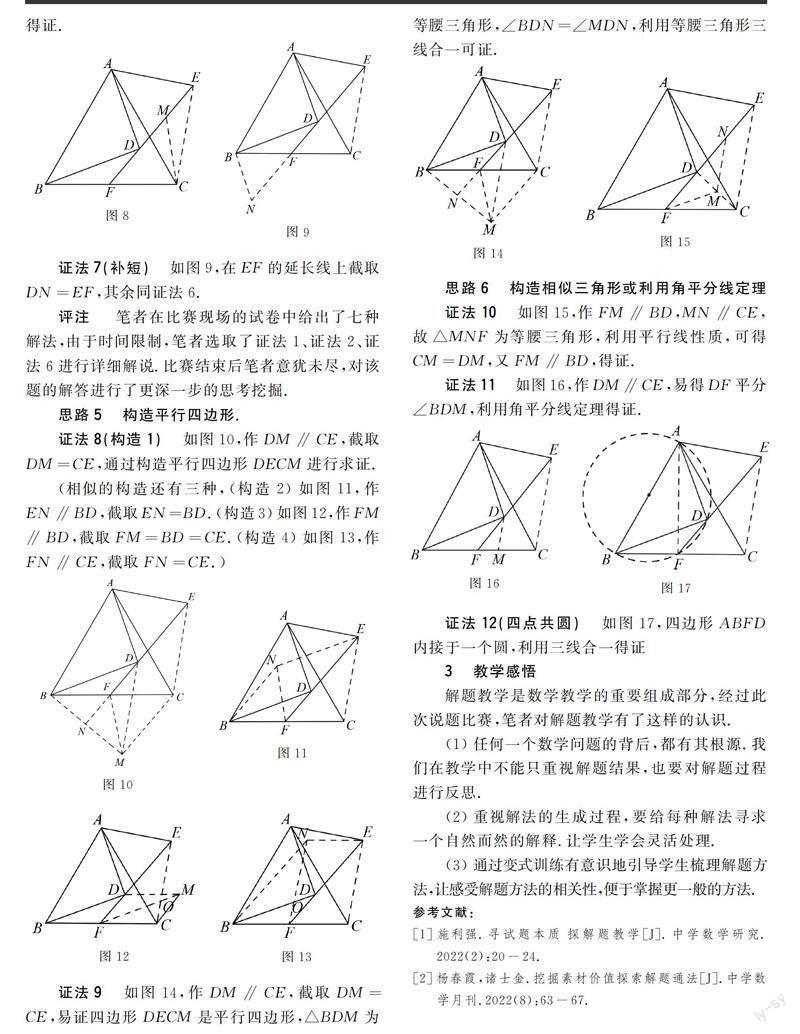
证法6（截长） 如图8，在EF上截取EM=DF，则△BDF≌△CEM，易得∠MFC=∠FMC，得证.

证法7（补短） 如图9，在EF的延长线上截取DN=EF，其余同证法6.

评注 笔者在比赛现场的试卷中给出了七种解法，由于时间限制，笔者选取了证法1、证法2、证法6进行详细解说.比赛结束后笔者意犹未尽，对该题的解答进行了更深一步的思考挖掘．

思路5 构造平行四边形.

证法8（构造1） 如图10，作DM∥CE，截取DM=CE，通过构造平行四边形DECM进行求证.

（相似的构造还有三种，（构造2）如图11，作EN∥BD，截取EN=BD.（构造3）如图12，作FM∥BD，截取FM=BD=CE.（构造4）如图13，作FN∥CE，截取FN=CE.）

证法9 如图14，作DM∥CE，截取DM=CE，易证四边形DECM是平行四边形，△BDM为等腰三角形，∠BDN=∠MDN，利用等腰三角形三线合一可证.

思路6 构造相似三角形或利用角平分线定理

证法10 如图15，作FM∥BD，MN∥CE，故△MNF为等腰三角形，利用平行线性质，可得CM=DM，又FM∥BD，得证.

证法11 如图16，作DM∥CE，易得DF平分∠BDM，利用角平分线定理得证.

证法12（四点共圆） 如图17，四边形ABFD内接于一个圆，利用三线合一得证

3 教学感悟

解题教学是数学教学的重要组成部分，经过此次说题比赛，笔者对解题教学有了这样的认识.

（1）任何一个数学问题的背后，都有其根源．我们在教学中不能只重视解题结果，也要对解题过程进行反思.

（2）重视解法的生成过程，要给每种解法寻求一个自然而然的解释．让学生学会灵活处理．

（3）通过变式训练有意识地引导学生梳理解题方法，让感受解题方法的相关性，便于掌握更一般的方法．

参考文献：

［1］施利强.寻试题本质 探解题教学[J].中学数学研究.2022（2）：20-24．

［2］杨春霞，诸士金.挖掘素材价值探索解题通法[J]．中学数学月刊.2022（8）：63-67．