高超声速火箭橇凿削磨损影响因素及临界条件研究

杨经纬,陈科儒,孙琨,陈诚

(1. 西安交通大学金属材料强度国家重点实验室,710049,西安;2. 中国兵器工业试验测试研究院,714200,陕西华阴)

火箭橇试验是用于模拟高速物体运行的测试装置,主要由轨道、滑靴、车体、动力系统和制动系统组成,如图1所示。通过动力系统推动车体在专有的轨道上高速运行,记录运动过程中产生的空气动力学信息,用以高端武器装备的研究和开发[1-3]。无润滑的靴-轨配副之间存在着高速的接触、碰撞过程,产生了剧烈的干滑动磨损现象[4-6]。当运动达到一定条件时,靴-轨配副材料发生深度融合,在表面形成了犹如泪滴状的蚀坑,如图2所示,此现象称为火箭橇试验的凿削磨损现象[7]。

图2 凿削磨损蚀坑Fig.2 Corrosion pits of gouging wear

不同于一般的干滑动磨损,凿削磨损具有更高的应变率,往往达到107s-1以上,靴-轨配副经历着巨大的非线性变形,高额的应变能致使变形区域温度骤然上升,材料变形抗力急剧降低,在巨大冲击力的持续作用下形成了凿削蚀坑[8-9]。Barker等[10]通过对凿削环境的计算,结合实际试验提出了凿削磨损的形成机理。Laird等[11-12]运用二维模拟程序CTH代码研究了温度对凿削磨损的影响,在一定的航向速度下,滑靴底面温度越高,凿削磨损越易发生,且凿削磨损的深度越大,凿削磨损的形成机制也与温度密切相关。Cinnamon等[13-14]进行了一系列的材料本构试验和热力学性能测试,修正了CTH计算模型,模拟了凿削磨损的形成过程,研究发现轨道的不平整度是影响凿削磨损的重要因素,并与试验进行了对比验证,证明了数值模拟的可靠性。

以往的研究中虽然能够阐释凿削磨损的部分机理,但并未系统地研究影响凿削磨损的多项相关因素,也未提出凿削磨损率的计算方法,同时,二维计算模型并不能完整反映出凿削磨损的形貌特点。针对上述问题,本文采用有限元的方法,建立了凿削磨损的三维有限元计算模型,对凿削磨损的影响因素及临界条件进行了研究,以期减少凿削磨损发生的可能性,为火箭橇试验系统提供安全、平稳的运行环境。

1 三维有限元凿削磨损模型

1.1 建模过程

使用有限元软件Abaqus建立三维凿削磨损模型如图3所示,该模型由轨道、轨道表面的微凸体以及滑靴组成。磨损现象最明显的尺度位于10-6～10-5m,因此将μm设置为单位尺寸。本文研究的重点是滑靴与微凸体在长度方向上的持续接触过程,为了提高计算效率,可以适当减小两部件在高度上的尺寸。为此,将滑靴的几何尺寸设置如下:长为 600 μm,高为20 μm,深为60 μm。轨道的几何尺寸设置如下:长为400 μm,高为20 μm,深为60 μm。根据Hale对轨道表面磨损形貌的研究,同时考虑到高速撞击下模型的计算稳定性,使用单一微凸体来模拟滑靴与轨道的摩擦接触过程,半径设置为6 μm。该微凸体位于轨道表面,顶端上方与滑靴底面相接触。

图3 三维有限元凿削磨损模型Fig.3 Three-dimensional finite element model of gouging wear

滑靴存在平行于X轴的航向速度v1和平行于Y轴的竖向速度v2,滑靴表面初始温度为Ts, 轨道表面初始温度为Tr。根据文献[15]中已知的火箭橇运动分析数据,航向速度从0变化至1 500 m/s时,竖向速度最大值为1.5 m/s。模拟时为保证凿削磨损的发生,在设置初参数时考虑降低航向速度与竖向速度的比值,即增加滑靴在每个单位水平运动距离内竖直向下移动的长度,因此将初参数设为:v1=1 200 m/s,v2=2 m/s,Ts=673 K,Tr=293 K。

1.2 接触区域网格划分

滑靴与微凸体的接触区域是发生凿削磨损的位置,该区域存在高额的塑性流变,对网格的质量要求较高。图4为接触区域轨道网格图,综合计算的精度和效率,设定接触区域的网格尺寸为0.75 μm,网格单元类型为C3D8RT,即八节点热耦合六面体单元。

图4 接触区域轨道网格图Fig.4 Grid diagram of contact area

1.3 热-力耦合场

高速运行的滑靴与轨道接触碰撞时会产生大量的摩擦热,摩擦热源在靴轨接触区域形成了温度场,持续加热接触区域的材料,使之变形抗力降低,这是一个热力耦合的过程。Abaqus中的热力耦合有顺序耦合与直接耦合两种方式[16]。顺序耦合着重于某一要素,另一要素作为条件而存在;直接耦合则是两要素的相互作用。火箭橇试验是一个温度场和应力场相互作用的结果,因此本文采用的是直接耦合法。

2 材料参数

2.1 Johnson-Cook本构模型

材料在高速、高应力和高温的工况条件下产生极端的非线性变形,使用Johnson-Cook本构模型可以很好地描述材料在这类工况下材料应力、应变与温度的关系。Johnson-Cook本构模型的表达式[17]如下

(1)

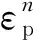
本文中使用的滑靴材料是Vascomax 300钢,轨道材料是AISI 1080钢。两种材料的Johnson-Cook本构模型参数见表1。

表1 滑靴与轨道材料Johnson-Cook本构模型参数

2.2 Johnson-Cook失效准则

极端变形条件下,材料经历弹塑性变形阶段后进入损伤变形阶段,伴随着材料屈服强度和弹性的消失,材料损伤直至失效,Johnson-Cook失效准则是对这一阶段材料行为的描述,其表达式[18]如下

(2)

式中:εf为材料失效应变;P为压强;q为米塞斯应力;d1～d5为材料失效参数。

表2是滑靴与轨道材料Johnson-Cook失效准则参数。

2.3 Mie-Gruneisen状态方程

在高速、高应变率的工况下,材料内部的应力波沿着运动方向进行传导,并对材料的接触属性产生影响。Mie-Gruneisen 状态方程用于描述此时材料压强、能量和温度、密度的关系[19]。Mie-Gruneisen状态方程的表达式为

(3)

式中:ρ0为参考密度;c0为参考声速;η为名义压缩应变;s为一个与线性冲击和粒子冲击相关的系数;Γ0为材料特性参数。

两种材料的状态方程参数见表3。

表3 滑靴与轨道材料Mie-Gruneise状态方程参数

2.4 摩擦系数动态方程

根据Montgomery[20-21]对火箭橇试验摩擦系数的研究,载荷与航向速度的乘积与摩擦系数存在联系。对试验数据进行拟合后可以得到以下的摩擦系数动态方程

μ=

(4)

式中:p为载荷;v为航向速度。

根据实际的工况条件,本文中将载荷设置为5 MPa,由此求出航向速度分别为1 200、1 600、1 800 m/s时摩擦系数为0.331、0.310、0.303。

2.5 热分配系数动态方程

运动初期摩擦生热均匀分布,随着运动的进行,滑靴表面的温度不断上升,而与滑靴接触的轨道表面温度一直等同于室温,二者之间存在的温度差导致了热分配系数的差异[22-24]。Le等[25]对火箭橇试验的热分配系数进行了研究,发现滑靴表面的热分配系数可以用一个有关于时间的动态方程加以描述,该方程的表达式如下

α(t)=0.4exp(-5t2)+0.1

(5)

计算式(5)发现运动开始时热分配系数为0.5,随着运动的进行,热分配系数逐渐减小,并在t为1 s后无限趋近于0.1。

3 凿削磨损有限元分析结果

3.1 凿削磨损过程

整个凿削磨损过程如图5所示,运动开始后,滑靴底面与微凸体发生持续接触碰撞过程,某一时刻滑靴底面材料超过最大变形极限而受到移除,凿削磨损开始发生。随着运动的进行,滑靴底部材料与微凸体材料形成了图5中红圈所示的嵌入型结构,该结构能够稳定地对滑靴底面造成破坏,此时凿削磨损持续发生。凿削磨损结束后,微凸体已经不具备破坏滑靴底部的几何结构,在滑靴底部可以观察到凿削磨损留下的泪滴状蚀坑。

图5 凿削磨损过程Fig.5 Gouging wear process

3.2 温度和应力结果

分别选取微凸体高度方向1/2处平行于X轴方向和滑靴底部与微凸体接触区域平行于X轴方向的路径,如图6所示,此时运动时间为7.5×10-8s。

图6 微凸体和滑靴采集路径Fig.6 Collection path of asperity and slipper

得到沿路径微凸体、滑靴温度和应力的变化如图7、图8所示。沿路径微凸体温度Ta先增大后减小,在路径中心位置S=4.2 μm处有最大值381.6 K,说明微凸体发生变形时,温升集中在中心区域;沿路径微凸体应力值σa持续上升,在最远端有最大值2 087.6 MPa。沿路径滑靴温度Ts快速上升后出现持续下降,在S=1.0 μm处有最大值1 632.1 K,此处为变形的核心区域;滑靴应力σs在路径开始位置具有最大值,沿路径方向下降至550 MPa左右保持不变,最后降低至238.1 MPa。显然,温度与应力之间存在相互作用,但并非简单线性的关系,二者的变化趋势在某些区域保持一致,但也存在完全相反的现象。

图7 沿路径微凸体温度和应力的变化 Fig.7 Temperature and stress changes of the asperity along the path

图8 沿路径滑靴温度和应力的变化Fig.8 Temperature and stress changes of the slipper along the path

根据Laird[12]使用CTH模型计算的结果,凿削时核心变形区域的最大应力约为8 000 MPa,最大温度约为1 600 K。由于该CTH模型设置的航向速度(v1=2 000 m/s)和竖向速度(v2=50 m/s)都远大于本文中使用的参数,发生凿削时将产生更大的应力聚集,但两种模型的应力量级相同,变形温度相当,且都能观察到靴轨材料的深度融合,证明了本文所建立的有限元凿削磨损模型的合理性。

3.3 凿削磨损率

当模型中的某一单元发生过量的塑性变形时,Abaqus会自动判定其变形量是否超过Johnson-Cook准则中的变形极限,超过变形极限的单元会被自动移除,统计不同时刻模型体积的变化可以计算出凿削磨损率的大小。本文中的失效单元总体积可由以下式计算得到

(1)地形地貌：高山出名茶的有利条件是多雨、温差大，从海拔高度来看，高海拔(>1 000 m)区气温过冷，日照时间偏长，不利于茶叶生长；低海拔(<200 m)区因气温偏高，茶树根部透水性差，也不利于茶树生长。

Vdamage=∑Vfractured_elements

(6)

式中:Vfractured_elements为超过最大变形量而失效的单元体积。

不同时刻失效单元的体积除以滑动的距离即可得到该时刻的凿削磨损率

(7)

式中:Ssliding为滑靴沿航向运动的距离。

计算多个时间点t上的滑靴凿削磨损率变化情况,得到图9所示的滑靴凿削磨损率曲线。在凿削磨损的初期阶段,滑靴磨损率随时间迅速上升,在运动的中期达到该阶段的最大值,并在之后有所下降。观察磨损率出现下降时段内的靴轨接触区域形貌,发现在这段时间并未出现凿削磨损现象。在运动过程的后期,凿削磨损率又一次上升,滑靴的底面出现了第二个凿削磨损蚀坑。以上结果说明凿削磨损或是一个多次性的非连续的破坏过程。

3.4 竖向速度变化对凿削磨损的影响

由于偏振作用,滑靴在竖直方向的运动速度称为竖向速度。竖向速度的大小与凿削磨损现象存在关联,为研究不同竖向速度对凿削磨损现象的影响,本项模拟共设置了6组不同的竖向速度,其他参数设置与初始条件一致,得到的不同竖向速度下凿削磨损的发生情况见表4。

表4 不同竖向速度下凿削磨损发生情况

表4中,v2=1.75 m·s-1是凿削磨损发生的临界值,只有当v2≥1.75 m·s-1时凿削磨损才会发生,这表明竖向速度的增加有利于凿削磨损的发生。

表5为不同竖向速度下凿削磨损发生距离和终止距离,其含义是凿削磨损发生(终止)位置与模型初始位置的直线距离。随着竖向速度的增加,凿削磨损的发生距离由54 μm减小至46 μm,终止距离由264 μm减小至217 μm。显然,存在着一个规律性的结论:随着竖向速度的增加,凿削磨损的发生距离和终止距离都会变小,但在v2= 2.25 m·s-1时有所不同,凿削磨损的发生距离最小,而终止距离最大,观察该速度下靴轨接触区域形貌,发现其形成了十分稳定的嵌入型结构,对滑靴底面的破坏持续时间最长,因此形成了最长的凿削蚀坑。

表5 不同竖向速度下凿削磨损的发生和终止距离

不同竖向速度下凿削磨损率曲线如图10所示,随着竖向速度增大,凿削磨损率上升,这是由于随着竖向速度增大,单位时间内滑靴的竖向位移增大,滑靴与微凸体的接触作用加深,受破坏而移除的单元数增多。v2= 2.25 m·s-1时也有所不同,该速度下的凿削磨损率最大,因其形成了最为稳定的嵌入型结构。

图10 不同竖向速度下凿削磨损率曲线 Fig.10 Gouging wear rate curve under different vertical velocities

3.5 温度变化对凿削磨损的影响

高应变率变形中,塑性变形功转变为热量,接触区域温度持续上升,材料受热而发生软化,影响凿削磨损现象的发生。本项模拟中设置了4组不同的滑靴温度以研究温度对凿削磨损现象发生的影响,结果见表6。发生凿削磨损时Ts≥673 K,表明温度的升高对凿削磨损的发生是有利的。

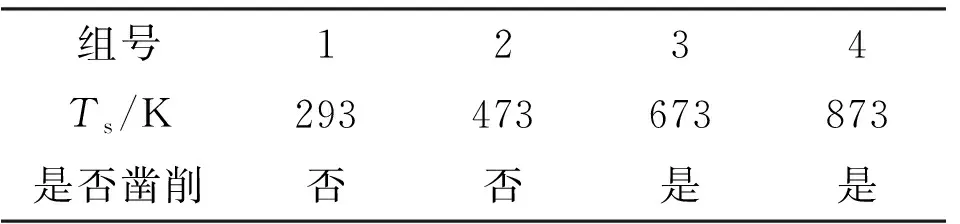
表6 不同温度下凿削磨损发生情况

表7为不同温度下凿削磨损发生和终止距离。随着温度增大,凿削磨损发生距离由54 μm减小至50 μm,凿削磨损的终止距离由264 μm增加至300 μm。这表明温度的升高不仅使凿削磨损的发生位置提前,同时使凿削磨损的结束位置置后。

表7 不同温度下凿削磨损的发生和终止距离

不同温度下凿削磨损率曲线如图11所示,凿削磨损率随温度的上升而提高,这是由于温升使材料软化,变形抗力下降,更易超过变形极限而被移除。

图11 不同温度下凿削磨损率曲线Fig.11 Gouging wear rate curve at different temperatures

3.6 凿削磨损临界条件计算

在某一确定的航向速度下,改变竖向速度和温度直到刚好能够发生凿削磨损,此时的竖向速度和温度条件即是凿削磨损的临界条件。不同航向速度下的临界条件见表8,可见随着航向速度增大,临界竖向速度和临界温度均上升。此外,航向速度和临界竖向速度的夹角也存在着一定的规律,随着航向速度的增大,夹角随之上升。

表8 凿削磨损临界条件

根据凿削磨损临界条件规律:航向速度越大,临界竖向速度和临界温度都将上升,即当单一航向速度提高而其他条件不发生改变时,凿削磨损将难以发生。在实际工况条件下,航向速度与竖向速度、温度之间存在一定的联系,随着航向速度的提高,滑靴所承受的载荷急剧上升,竖向速度因此增大,由摩擦生热和气动传热所带来的温度场使滑靴表面的温度迅速上升,极易达到这两个条件的临界值。要想有效避免火箭橇试验凿削磨损的发生,必须控制滑靴竖向速度和温度的大小,通过结构优化设计和涂层包覆等手段可达到此目的。

4 结 论

本文通过建立三维有限元凿削磨损模型,对凿削磨损温度-应力状态、影响因素以及临界条件进行研究,得到了以下结论。

(1)沿路径微凸体温度先增大后减小,在中心位置有最大值;沿路径微凸体应力持续增大,在路径最远端处有最大值。沿路径滑靴温度快速上升后下降,滑靴应力最大值在路径开始位置。温度与应力存在相互作用,二者的变化趋势在某些区域保持一致,但也存在相反的现象。

(2)竖向速度的增大有利于凿削磨损的发生。一般而言,凿削磨损发生距离和终止距离都随竖向速度增大而减小,凿削磨损率随竖向速度增大而上升,但是也存在特例,因在这一速度条件下形成了最为稳定的嵌入型结构。

(3)温度的上升有利于凿削磨损的发生,随着温度上升,凿削磨损发生距离减小而终止距离增大,凿削磨损率也随之上升。

(4)随着航向速度的增大,凿削磨损临界竖向速度和临界温度增大,航向速度和临界竖向速度夹角也随之上升。通过降低滑靴竖向速度和温度能有效避免凿削磨损的发生。