空间组合弯头气固两相流动磨损特性的数值模拟

王 宇， 刘荣堂， 刘 明， 严俊杰

(西安交通大学 动力工程多相流国家重点实验室， 西安 710049)

目前，燃煤火力发电是我国最主要的电力来源。燃煤电厂的烟气和煤粉管道中存在大量的换热管道和弯头结构[1]，气体携带飞灰或煤粉等固体颗粒流经管道时，固体颗粒不停冲刷管壁，对管壁尤其是弯头处壁面产生了严重的冲蚀磨损[2]，威胁到电厂运行的安全性和可靠性。在燃煤机组烟风煤粉管道的布置过程中，往往需要进行空间转弯，此时需将2个弯头连接，形成特殊的空间组合弯头结构。空间组合弯头结构由于其弯头间连接长度有限，导致弯头间发生耦合作用，使空间组合弯头内气固两相流动及磨损特性不同于单个弯头部件。

许多学者针对气固或液固两相流管道的磨损进行了数值模拟[3-6]，并验证了磨损预测精度[7-8]。Chen等[9]针对稀相气固两相流流经90°弯头和T形管时的磨损特性进行了研究，并比较了T形管与弯头的相对磨损程度。谢振华等[10-11]对90°方形截面弯头内导流板的个数及安装位置进行了优化，得出导流板的最佳安装方案。Duarte等[12]提出一种在弯头外侧加装涡流腔的新型弯头，可减轻壁面磨损。El-Behery等[13]采用数值模拟方法对180°弯头的磨损进行了预测，并研究了颗粒尺寸对撞击弯头位置的影响。Zhou等[14]研究了颗粒形状、涡流强度和弯头方向对管壁磨损率的影响。

针对管道壁面磨损的研究中，研究对象多选取90°方截面或圆截面弯头、T形管或U形管。但是，针对空间组合弯头内气固两相流动磨损特性的研究鲜有报道。笔者采用数值模拟方法对空间组合弯头结构内气固两相流动及磨损特性进行了研究，并分析了气流速度、颗粒浓度及颗粒直径对管壁磨损率的影响。

1 物理模型

图1为空间组合弯头结构的几何模型。其中，截面直径D=60 mm，缓转弯头的弯径比R/D=1.5，R为转弯半径。为消除空间组合弯头上下游效应的影响，设置L1=L2=20D=1 200 mm，L1和L2分别为出、入口直管段长度，L为两弯头间连接长度。

2 计算模型及方法

2.1 计算模型

采用半经验磨损预测模型[15-16]计算管壁磨损率E。

(1)

式中：A为经验常数；HB为材料的布氏硬度；Fs为颗粒形状系数，对于球形颗粒，取值为0.2；Vp为颗粒碰撞的速度；n为速度指数，取值为1.73；f(θ)为撞击角函数。

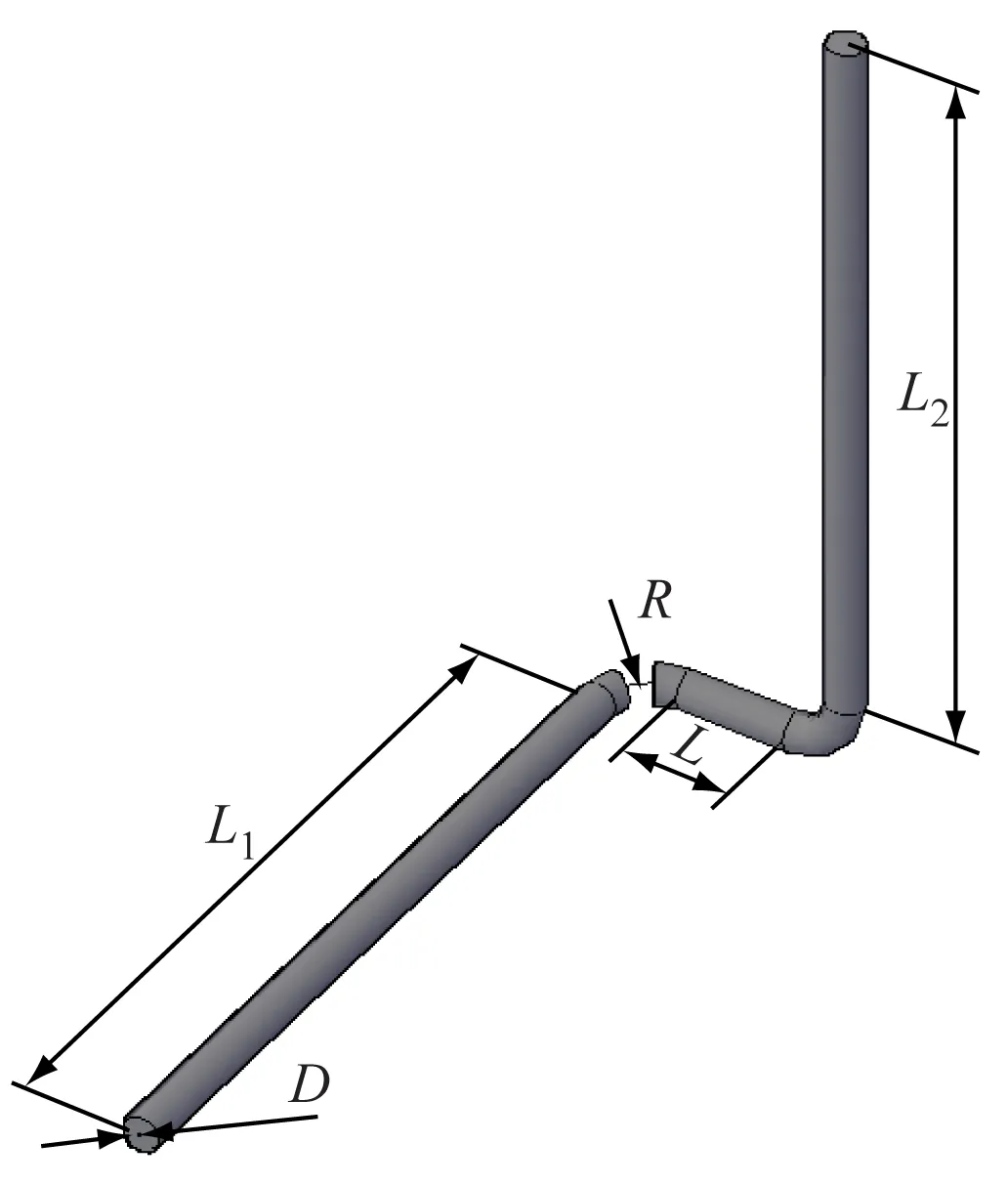
图1 空间组合弯头的几何模型

(2)

式中：θ0、a、b、w、x、y、z均为取决于靶材的经验常数。

对于碳钢，经验常数取值见表1。

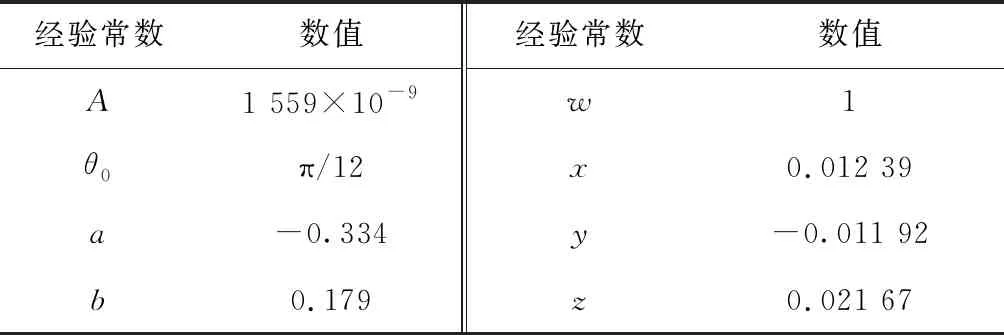
表1 经验常数

通过编制用户自定义函数(UDF)，预测管壁磨损率。

2.2 气固两相流模型

采用基于欧拉-拉格朗日方法的离散相(DPM)模型求解管道内气固两相流场。在DPM模型中，将气相作为连续相处理，将颗粒相作为离散相处理。在DPM模型中，定义主相为空气，选取入口速度V=15 m/s[17]；第二相为球形颗粒，球形固体颗粒从入口截面喷射进入计算域，选取颗粒密度ρp=2 650 kg/m3，并定义颗粒浓度φ为固体颗粒质量流率与空气质量流率之比；出口设定为表压pout=0 Pa的压力边界，内壁面设定为绝对粗糙度K=0.04 mm的无滑移固壁边界。管道内流动为湍流流动，采用标准k-ε模型计算管道内湍流流场。

为准确计算颗粒对指定固体壁面的冲蚀磨损，首先采用DPM模型求解颗粒的运动轨迹，包括求解颗粒撞击固体壁面边界后发生反弹所形成轨迹及其速度变化。采用反弹经验公式[18]来预测颗粒与壁面的碰撞过程。

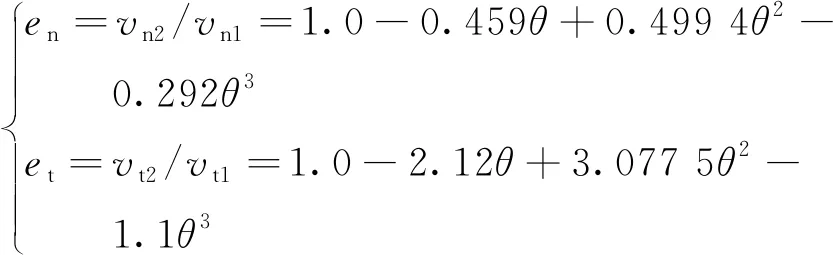
(3)

式中：en为法向恢复系数；et为切向恢复系数；vn1、vn2分别为颗粒撞击管壁前、后的法向分速度；vt1、vt2分别为颗粒撞击管壁前、后的切向分速度。

2.3 网格划分

利用ANSYS ICEM CFD软件进行全局结构网格划分，对管道截面划分o-block，并对壁面区域网格进行局部加密，模型的网格划分见图2。

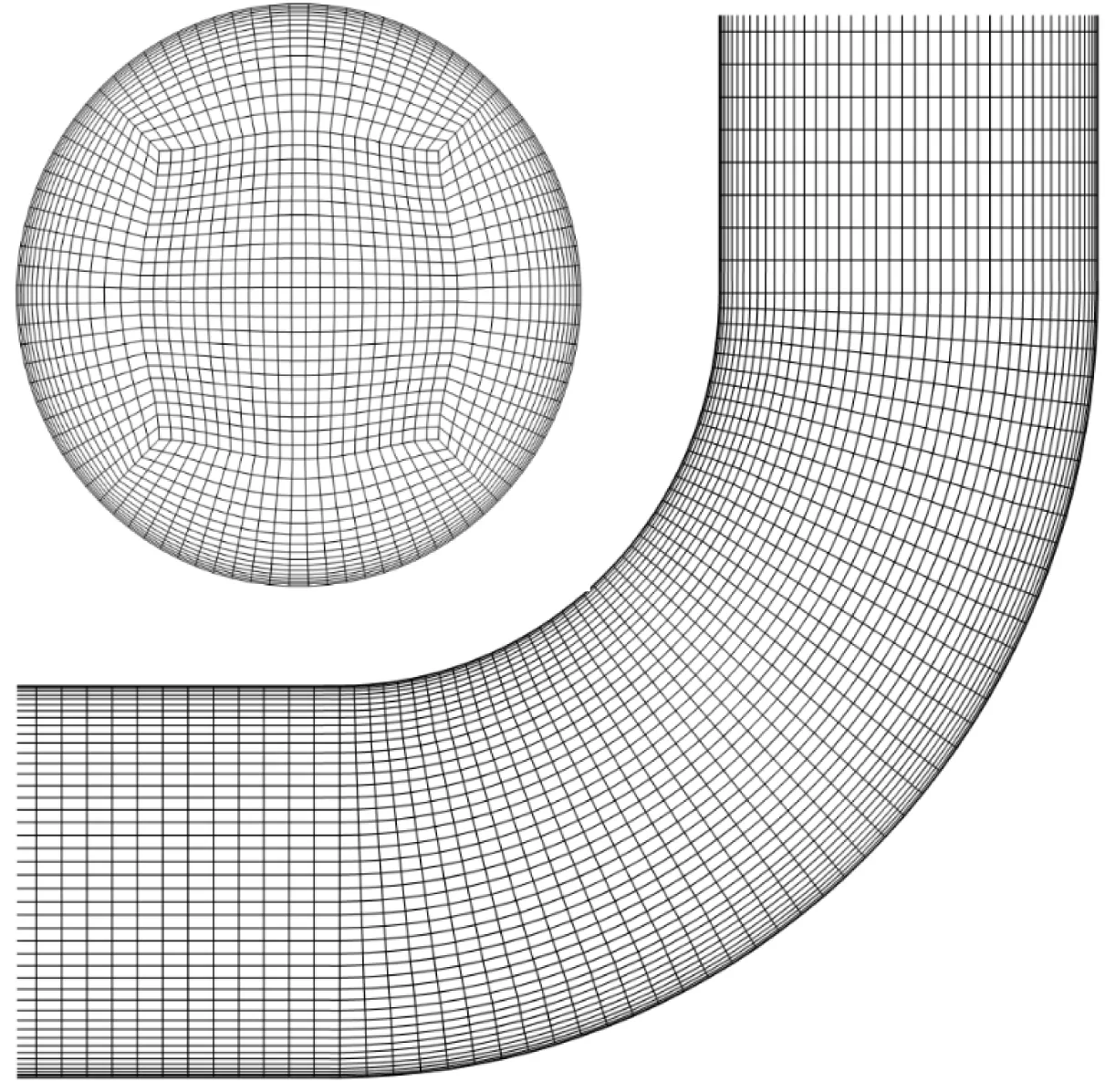
图2 网格划分示意图

2.4 数值模型的验证

采用实验数据[19]来验证模型的准确性。校验参数均来源于实验，如表2所示。在实验过程中，研究对象取直径为41 mm、转弯半径为133.25 mm的90°弯头。

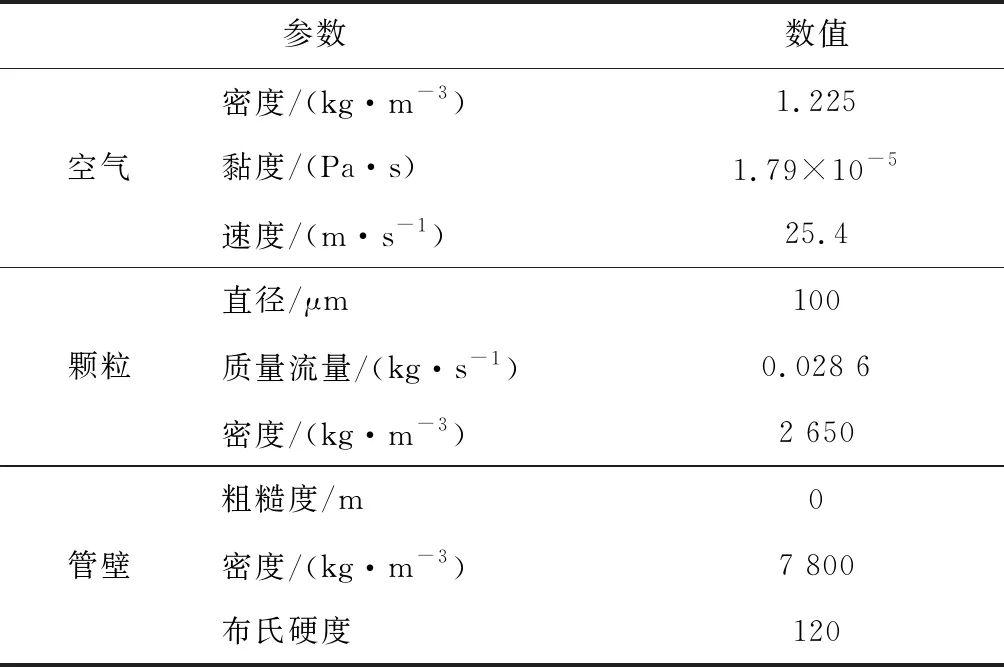
表2 校验参数

模型的验证结果见图3。由图3可知，磨损率和最大磨损位置的模拟结果与实验结果[19]均吻合良好，说明模型和计算方法正确可信。

图3 磨损率模拟结果与实验结果的对比

3 结果与分析

针对连接长度L/D=3[17]的典型空间组合弯头，研究不同气流速度、颗粒浓度和颗粒直径下空间组合弯头壁面磨损率分布和最大磨损率的变化规律，并将其与单个弯头进行对比。

3.1 空间组合弯头壁面磨损率分布

图4给出了在V=15 m/s、颗粒直径dp=100 μm、φ=1.89下空间组合弯头内各典型截面的速度云图。从图4可以看出，在空间组合弯头内第1个弯头速度分布基本对称，弯头内侧速度较大且发生分离；第2弯头的速度分布出现明显的不对称性，其内侧流速较大，出口高速流动区域转移至弯头外侧。

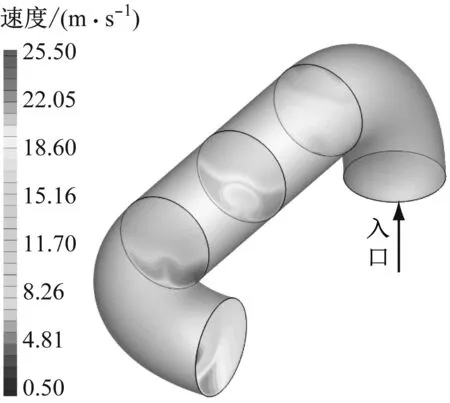
图4 空间组合弯头内各典型截面的速度云图

空间组合弯头内颗粒分布规律见图5。颗粒进入第1个弯头时会撞击到弯头外侧壁面，颗粒分布基本对称。在弯头内侧形成无颗粒区域，颗粒流出第1个弯头后无颗粒区域范围缩小。在颗粒进入第2个弯头后也会形成1个无颗粒区域，但由于第2个弯头的空间转弯，导致其内部颗粒分布不对称，更多的颗粒集中在远离管道入口的一侧。

图6给出了单个弯头和空间组合弯头管壁磨损率云图。单个弯头与空间组合弯头内第1个弯头的磨损率分布非常相似。颗粒由于惯性直接撞击到弯头外侧壁面，造成严重磨损，磨损率对称分布，磨损率自中心向四周逐渐减小。第2个弯头磨损率分布不对称，靠近管道入口的一侧磨损较轻。

(a) 第1个弯头

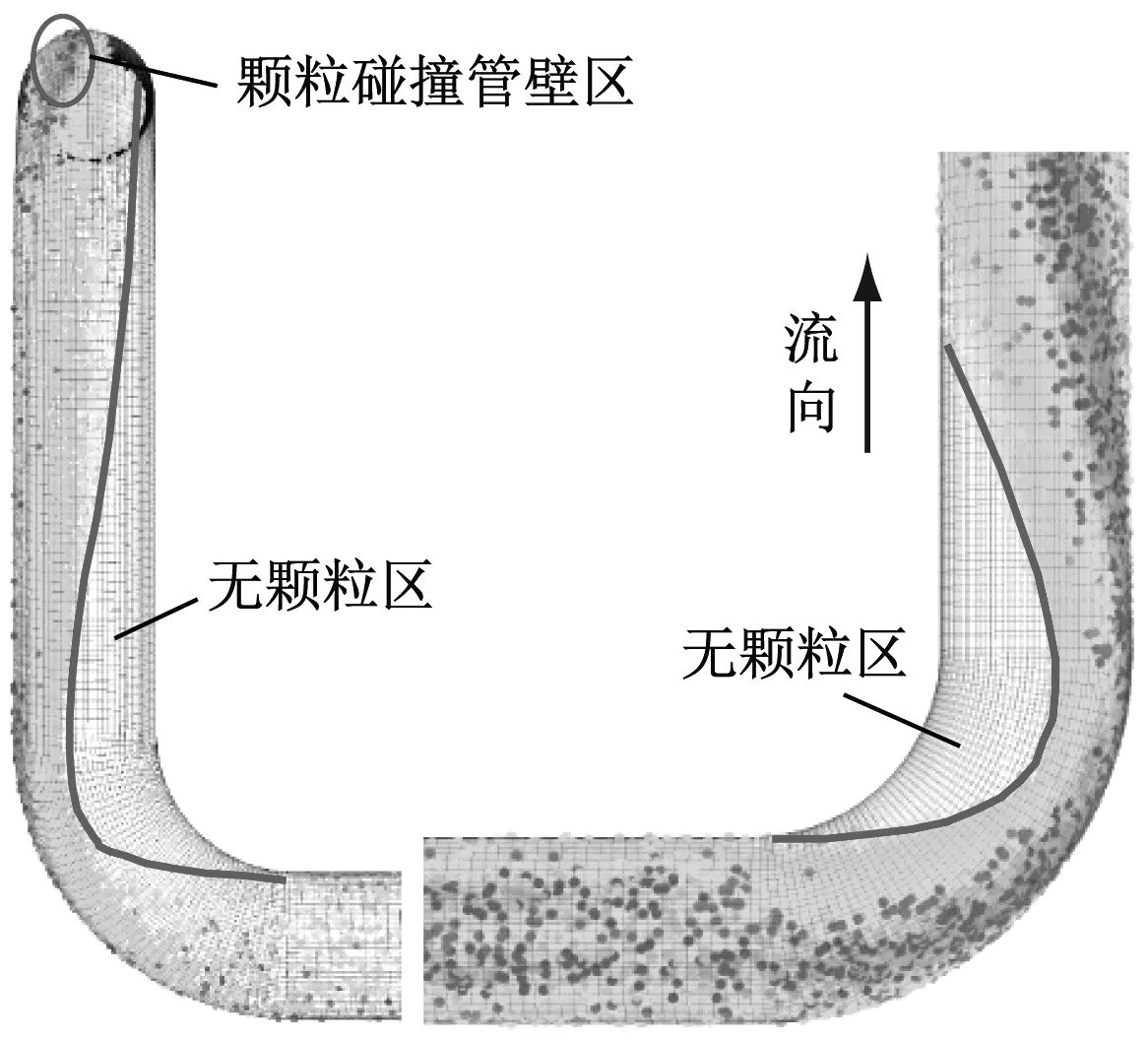
(b) 第2个弯头

图7给出了空间组合弯头外侧壁面磨损率随转弯角的变化规律。结果表明，随着转弯角逐渐增大，第1个弯头的磨损率在55°转弯角左右达到最大，随后磨损率迅速降低。第2个弯头的磨损率随转弯角的增大也呈先提高后降低的趋势，但最大磨损率出现在50°转弯角左右。整体上看，第2个弯头的磨损率低于第1个弯头。这是因为颗粒撞击到第1个弯头后损失了部分动能。

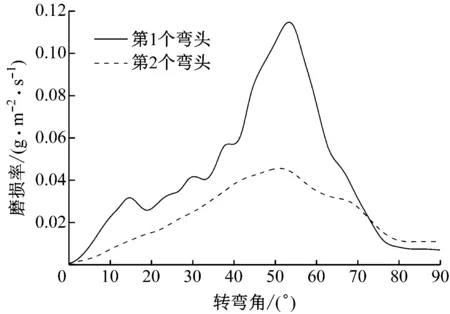
图7 空间组合弯头外侧壁面磨损率随转弯角的变化规律

图8给出了不同连接长度下空间组合弯头内第1个弯头和第2个弯头磨损率的分布情况。从图8可以看出，连接长度对第1个弯头的磨损率影响较小。这是因为颗粒进入弯头后由于惯性直接撞击在管壁上，进而造成磨损，连接长度对其影响较小。对于第2个弯头，不同的连接长度导致颗粒进入第2个弯头时与壁面的碰撞位置和碰撞角不同，造成第2个弯头磨损程度及其分布情况变化较大。随着连接长度的增加，第2个弯头的磨损严重区域增加，且由远离管道入口一侧渐渐向另一侧扩大。

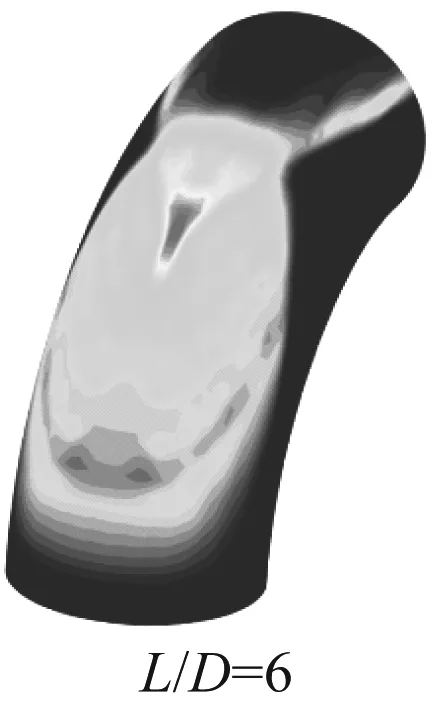
(a) 第1个弯头

(b) 第2个弯头

3.2 气流速度对空间组合弯头壁面磨损率的影响

在颗粒直径dp=100 μm、颗粒浓度φ=1.89的条件下空间组合弯头最大磨损率随气流速度的变化规律见图9。从图9可以看出，第1个弯头和第2个弯头的最大磨损率随气流速度的增大呈指数提高。这是由于气流速度增大会导致颗粒以更大的速度和动能撞击管壁，使磨损程度加重。

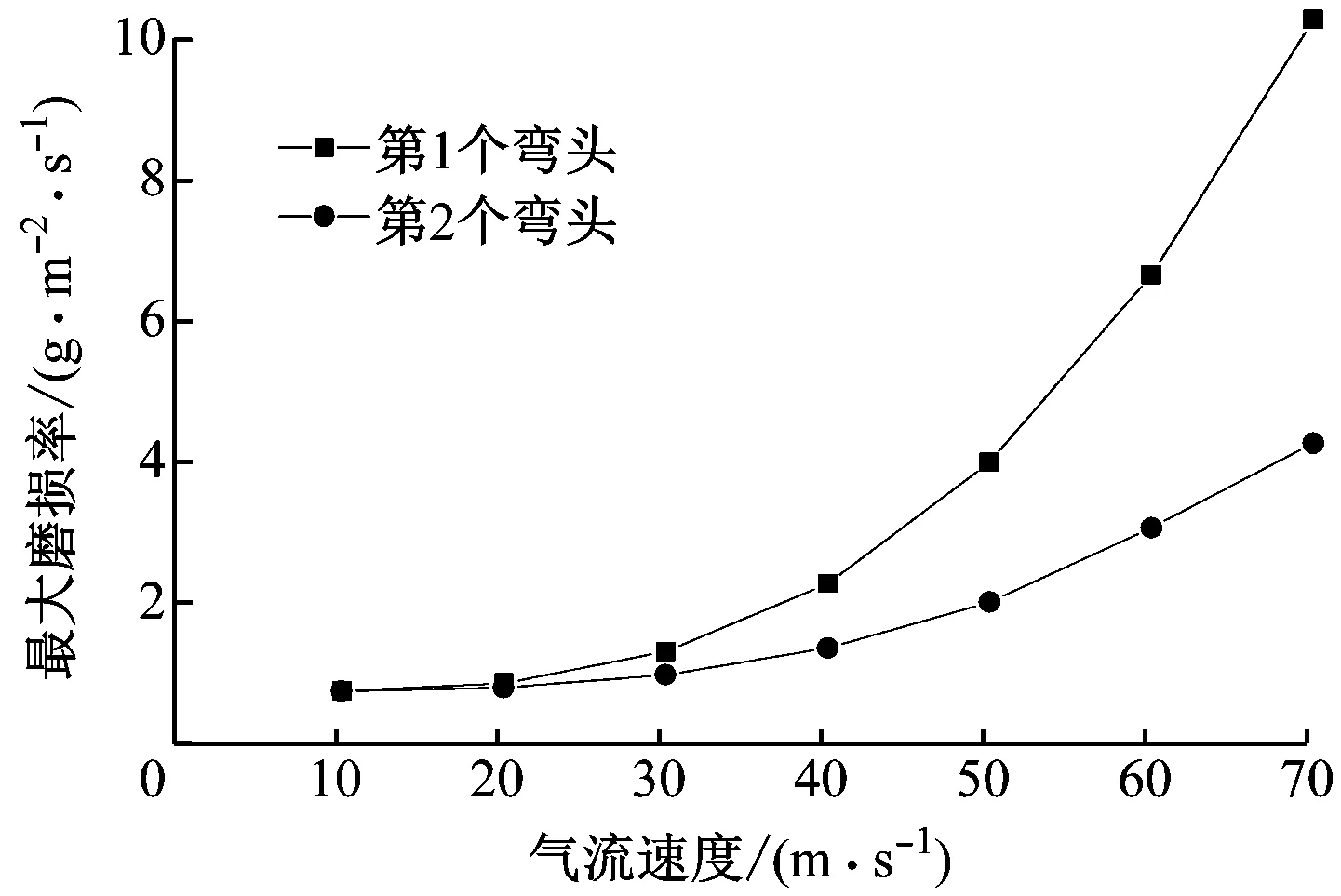
图9 空间组合弯头最大磨损率随气流速度的变化规律

3.3 颗粒浓度对空间组合弯头壁面磨损率的影响

在气流速度V=15 m/s、颗粒直径dp=100 μm的条件下空间组合弯头最大磨损率随颗粒浓度的变化规律见图10。从图10可以看出，第1个弯头和第2个弯头的最大磨损率随颗粒浓度的增大而线性提高。这是因为随着颗粒浓度的增大，颗粒撞击壁面的频率提高，进而磨损率提高。

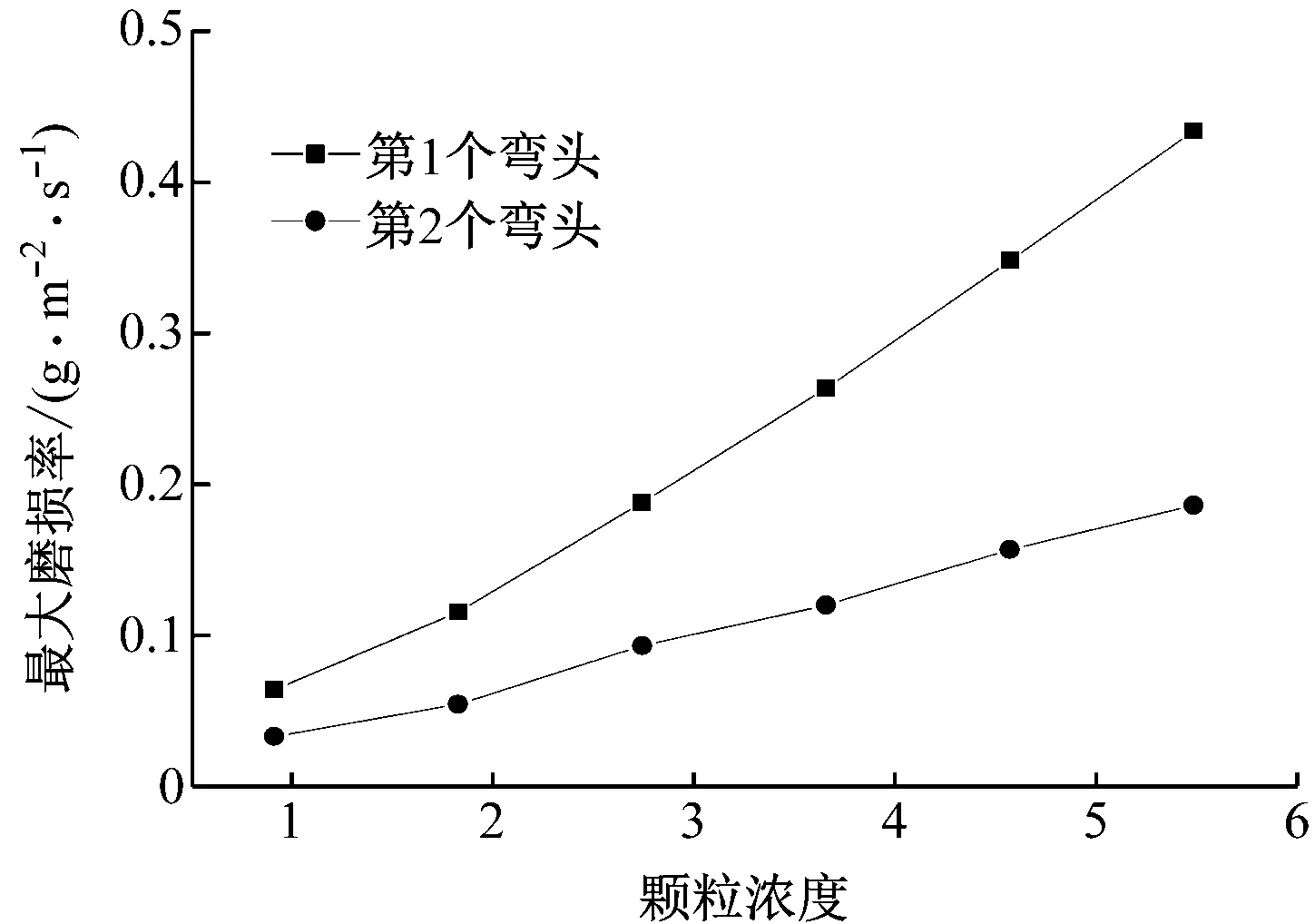
图10 空间组合弯头最大磨损率随颗粒浓度的变化规律

3.4 颗粒尺寸对空间组合弯头壁面磨损率的影响

斯托克斯数St是颗粒松弛时间与流动特征时间之比，在气固两相流的流动中反映了颗粒的跟随性。

(4)

式中：μ为动力黏性系数，Pa·s。

在气流速度V=15 m/s、颗粒浓度φ=1.89的条件下，空间组合弯头最大磨损率随颗粒St的变化规律见图11。从图11可以看出，第1个弯头的最大磨损率随St的增大先提高，后变化逐渐平缓；第2个弯头的最大磨损率随着St的增大先提高后降低。图12给出了不同颗粒直径下第1个弯头最大磨损率随转弯角的变化规律。结果表明，颗粒直径越小，最大磨损率对应的转弯角越大。这是由于颗粒直径较小时，颗粒跟随性较好，小颗粒跟随气流进入弯头，撞击壁面位置后移。对比颗粒直径为150 μm和250 μm的情况可以发现，两者最大磨损率出现位置几乎相同，且数值相近。

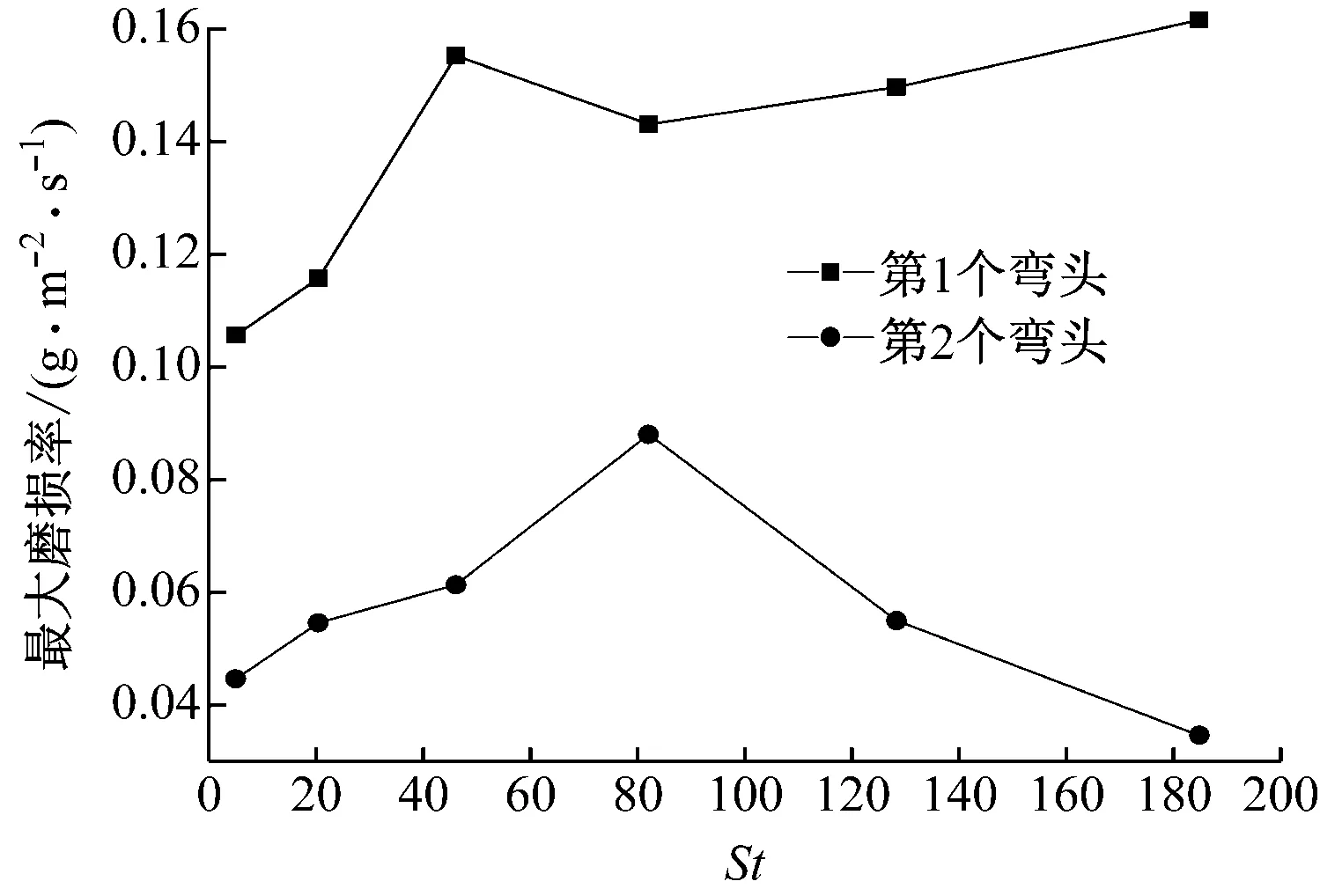
图11 空间组合弯头最大磨损率随St的变化规律

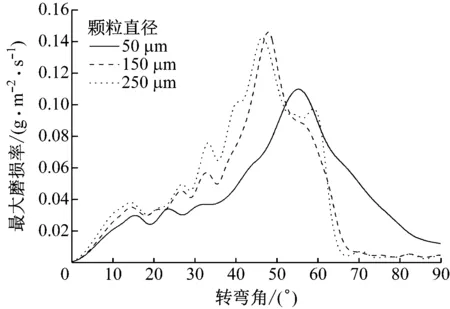
图12 第1个弯头壁面最大磨损率随转弯角的变化规律

4 结 论

(1) 第1个弯头的磨损率随转弯角的增大逐渐提高，在转弯角为55°左右达到最大，随后磨损率迅速降低。磨损最严重区域位于弯头外侧，磨损率分布由最严重位置向周围逐渐减小。第2个弯头的磨损率整体小于第1个弯头，这是由于颗粒与第1个弯头发生碰撞后损失了部分动量和动能。第2个弯头的磨损率和磨损位置不同于第1个弯头，在采取防磨措施时应予以考虑。

(2) 弯头间连接长度对第1个弯头的磨损率影响较小，但随着连接长度的增大，第2个弯头的磨损区域扩大。随着气流速度的增大，最大磨损率呈指数提高；随着颗粒浓度的增大，最大磨损率呈线性提高；随着颗粒St的增大，第1个弯头的最大磨损率先提高后变化逐渐平缓，第2个弯头的最大磨损率先提高后降低。